-
Analyse 2
-
1. Hoofdstuk 4 Eigenschappen van continue en afleidbare functies
- Theorie
- Theorie
- Theorie
This activity is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original activity or create your own copy for this Book instead?
This activity was created by '{$1}'. Do you want to modify the original activity or create your own copy instead?
This activity was created by '{$1}' and you lack the permission to edit it. Do you want to create your own copy instead and add it to the book?
Analyse 2
Jansen Karlijn, Oct 18, 2016
Afgeleiden Eigenschappen en toepassingen
Table of Contents
- Hoofdstuk 4 Eigenschappen van continue en afleidbare functies
- Theorie
- Theorie
- Theorie
Theorie
Bekijk de applet: Differentiaalquotiënt.
Je ziet een deel van de grafiek van de functie y = f(x).
Sleep het blauwe punt ∆x.
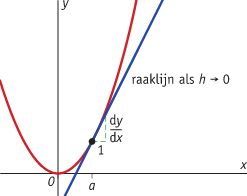
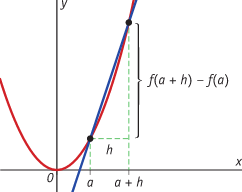
De gemiddelde verandering van de functie f op het interval [a,b] is:
De verandering in een punt met x = a van de functie f vind je door het differentiequotiënt op [a,a+h] te berekenen, waarbij je h steeds dichter bij 0 kiest:.
Voor x = a krijg je dan een rij met differentiequotiënten. Deze rij benadert een bepaald getal. Dit getal heet het differentiaalquotiënt voor x = a.
In plaats van voor x = a, schrijf je ook wel
In de grafiek is het differentiaalquotiënt gelijk aan:
- de richtingscoëfficiënt van de raaklijn in het punt van de grafiek met x = a
- de helling van de grafiek in het punt x = a
- de snelheid waarmee y verandert voor x = a
Saving…
All changes saved
Error
A timeout occurred. Trying to re-save …
Sorry, but the server is not responding. Please wait a few minutes and then try to save again.