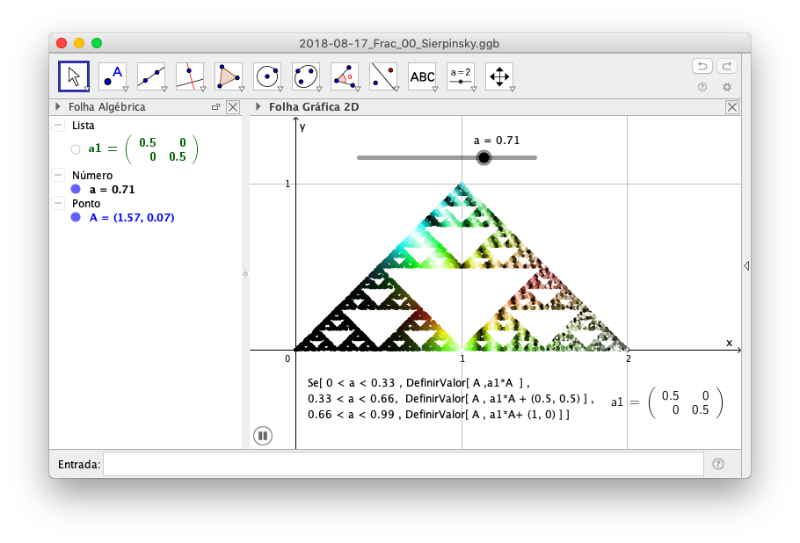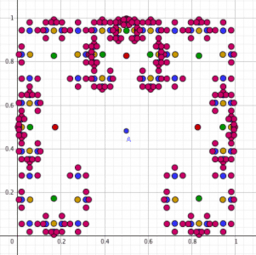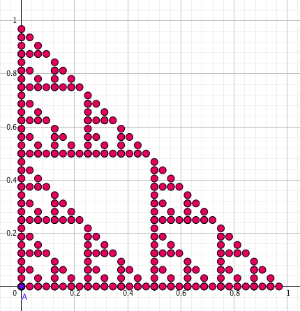
Iterated function system 3 afine maps.
The attractor of the iterated function system given by the set of 3 affine maps. That app show five generations. In an interactive way, it is possible to change the matrices of the related transformations and to see the respective attractors.
The Sierpinski triangle

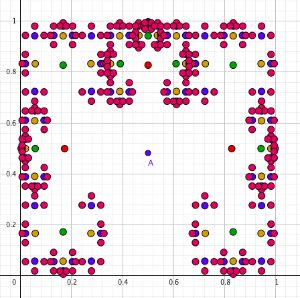
The Sierpinski triangle from a slide in GeoGebra.