FUNGSI KUADRAT
• Fungsi kuadrat dengan tabel, grafik, dan persamaan • Sifat-sifat fungsi kuadrat • Nilai maksimum • Nilai minimum • Pemecahan masalah melibatkan sifat-sifat fungsi kuadrat
Table of Contents
- Fungsi kuadrat dengan tabel, grafik, dan persamaan
- Fungsi Kuadrat
- Sifat-sifat fungsi kuadrat
- Grafik Fungsi Kuadrat
- Grafik Fungsi Kuadrat
- Pemecahan masalah melibatkan sifat-sifat fungsi kuadrat
- GRAFIK FUNGSI KUADRAT
Fungsi Kuadrat
Pertanyaan Pemantik
[list=1][*]Apa yang terjadi saat bola dilempar ke atas lalu jatuh kembali?[/*][*]Bagaimana pengaruh nilai [b]a[/b] pada arah grafik y = ax²?[/*][*]Kapan fungsi kuadrat mencapai nilai maksimum atau minimum?[/*][*]Apa makna titik potong grafik dengan sumbu X dan Y?[/*][/list]
Siswa dapat memahami nilai fungsi kuadrat
Siswa dapat memahami gambar fungsi kuadrat
Siswa dapat memahami konsep grafik fungsi f(x)=x^2 dan g(x)=(x-a)^2
Siswa dapat memahami konsep grafik fungsi f(x)=x^2 dan g(x)=x^2+k
Siswa dapat memahami konsep fungsi kuadrat dengan bentuk y=(x-a)^2+b
Grafik Fungsi Kuadrat
GRAFIK FUNGSI KUADRAT
Bentuk umum fungsi kuadrat adalah[br][math]f\left(x\right)=ax^2+bx+c[/math][br][br]dengan a, b, dan c bilangan real dan a[math]\ne[/math]0[br][br]Grafik fungsi kuadrat merupakan sebuah kurva yang berbentuk parabola dengan persamaan y=f(x).[br]karena [math]f\left(x\right)=ax^2+bx+c[/math]maka persamaan parabola itu adalah [math]y=ax^2+bx+c[/math][br][br]Untuk memahami grafik fungsi kuadrat, pelajarilah applet berikut
Siswa dapat memahami grafik fungsi kuadrat
Siswa dapat memahami pengaruh nilai a, b, dan c pada grafik fungsi kuadrat dengan bentuk umum f(x)=ax^2+bx+c
Siswa dapat memahami pengaruh nilai a, b, dan c pada grafik fungsi kuadrat dengan bentuk umum f(x)=ax^2+bx+c
Siswa dapat memahami grafik fungsi kuadrat
Hasil Pengamatan
Setelah kalian mengubah-ubah nilai a, b, dan c dengan cara menggeser slider. [br]Apa yang dapat kalian simpulkan tentang Grafik Fungsi Kuadrat?[br]Jawablah pertanyaan berikut![br][br]1. Bagaimana bentuk kurva grafik saat [br] * nilai a>0 maka kurva grafik terbuka ke .......[br] * nilai a<0 maka kurva grafik terbuka ke .......[br] * nilai a=0 maka kurva grafik berbentuk .......[br][br]2. Dimana letak titik puncak grafik terhadap sumbu Y saat[br] * nilai b>0 maka titik puncak grafik berada di sebelah ....... sumbu y[br] * nilai b<0 maka titik puncak grafik berada di sebelah ....... sumbu y[br] * nilai b=0 maka titik puncak grafik berada ....... sumbu y[br][br]3. Bagaimana titik potong grafik di sumbu Y terhadap titik O(0,0) saat[br] *nilai c>0 maka titik potong grafik terhadap sumbu Y berada di ....... titik O(0,0)[br] *nilai c<0 maka titik potong grafik terhadap sumbu Y berada di ....... titik O(0,0)[br] *nilai c=0 maka titik potong grafik terhadap sumbu Y berada ....... titik O(0,0)
Siswa dapat menentukan fungsi kuadrat dari suatu grafik fungsi kuadrat
GRAFIK FUNGSI KUADRAT
Tujuan Pembelajaran
[list=1][*][size=85]Mampu menentukan titk poton[/size][size=85]g sumbu x dan y serta titik puncak berdasarkan persamaan grafik fungsi kuadrat[/size][/*][size=100][size=85][*]Mampu Memecahkan masalah kontekstual yang berkaitan dengan grafik Fungsi Kuadrat[/*][*]Mampu Menganalisis Pengaruh Parameter a, b, dan c terhadap grafik dalam Persamaan Bentuk Umum Fungsi Kuadrat[/*][*]Mampu menyimpulkan bentuk grafik berdasarkan karakteristik dan persamaan grafik fungsi kuadrat[br][/*][/size][/size][/list]APERSEPSI
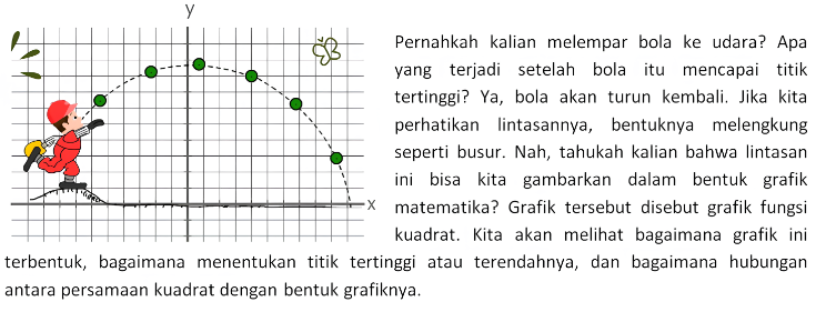
[justify][/justify]
MATERI SINGKAT
[justify][size=85][/size]Fungsi kuadrat merupakan fungsi yang berbentuk y = ax2+ bx + c, dengan a ≠ 0. Grafik dari fungsi kuadrat menyerupai parabola, sehingga dapat dikatakan juga sebagai fungsi parabola.[/justify]
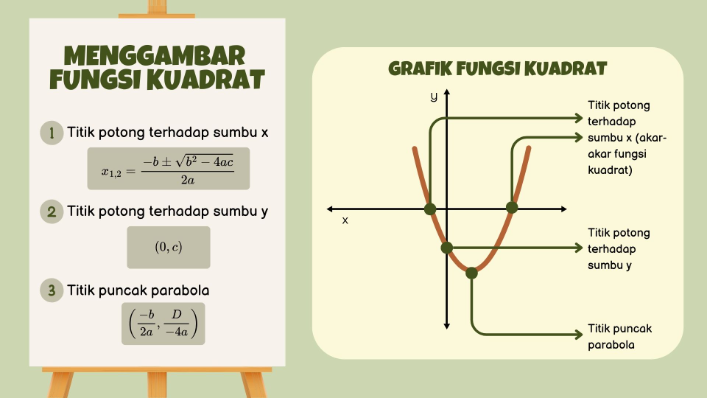
[br][b][size=200][size=150]PETUNJUK PENGGUNAAN MEDIA [/size][/size][/b][size=200][size=150][size=85][list=1][*]Perhatikan tiga kotak angka yang menunjukkan nilai a, b, dan c. [/*][*]Klik tombol ANIMASI a, ANIMASI b, atau ANIMASI c untuk melihat perubahan otomatis nilai tersebut dan pengaruhnya pada grafik.[/*][*]Jika ingin mengubah nilai secara manual, ketik angka yang diinginkan pada kotak a, b, dan c atau bisa juga dengan menggeser slider yang ada pada grafik. [/*][*]Klik tombol STOP untuk menghentikan animasi perubahan nilai koefisien.[/*][*]Klik tombol RESTART untuk mengembalikan semua nilai ke kondisi awal.[/*][/list][/size][/size][/size]
LEMBAR KERJA PESERTA DIDIK
[b][justify]Petunjuk Pengerjaan LKPD[/justify][/b][size=85]1. Isilah identitas kalian pada kolom yang telah diberikan[br]2. Bacalah setiap petunjuk pada LKPD untuk menyelesaikan latihan yang diberikan[br]3. Selesaikan secara berurutan setiap kegiatan pada LKPD[br]4. Gunakan media yang disediakan untuk menjawab soal latihan[br]5. Berikan jawaban yang tepat sesuai dengan kemampuan kalian[/size]
[b][color=#741b47][i][size=150]Nama:[br]Kelas:[/size][/i][/color][/b]
..
[br]
Soal 1
Jika diberikan persamaan kuadrat [math]y=\text{2x^2-4x+3}[/math]. Tentukan titik puncak dari grafik fungsi kuadrat tersebut?
Soal 2
Diketahui persamaan grafik fungsi kuadrat [math]f\left(x\right)[/math] adalah [math]f\left(x\right)=2x^2+4x-5[/math]. Titik potong grafik fungsi kuadrat terhadap sumbu [math]Y[/math] adalah...
Soal 3
Titik potong grafik fungsi kuadrat [math]f\left(x\right)=x^2-2x-8[/math] terhadap sumbu [math]X[/math] adalah...
Soal 4
Seorang pemain basket melempar bola ke arah ring dengan lintasan yang membentuk parabola. Lintasan bola dimodelkan dengan[br]persamaan: [br][center][math]y=-x^2+6x+8[/math][/center]di mana: [br][list][*][math]y[/math] adalah ketinggian bola (dalam meter) dari tanah,[/*][*][math]x[/math] adalah jarak horizontal bola dari titik lemparan (dalam meter)[/*][/list]Berapa tinggi maksimum yang dicapai bola?
Soal 5
Diketahui fungsi kuadrat [math]g\left(x\right)=-x^2+2x+7[/math]. Titik potong grafik fungsi ini dengan sumbu-Y adalah...
Soal 6
Seorang pemain sepak bola menendang bola ke udara sehingga membentuk lintasan parabola. Ketinggian bola terhadap tanah setelah t detik dinyatakan dengan persamaan:[br][center][math]h\left(t\right)=-2t^2+8t+3[/math][/center]dengan [math]h\left(t\right)[/math] adalah ketinggian bola dalam meter dan [math]t[/math] adalah waktu dalam detik sejak bola ditendang.[br]Berapakah ketinggian maksimum yang dapat dicapai oleh bola?
Soal 1
Berdasarkan pengamatan anda terhadap grafik fungsi kuadrat[br]yang muncul pada media di atas, bagaimana bentuk grafik fungsi kuadrat jika[br]a>0?
Soal 2
Berdasarkan pengamatan anda terhadap grafik fungsi kuadrat[br]yang muncul pada media di atas, bagaimana bentuk grafik fungsi kuadrat jika[br]a<0?[br][br][br]
Soal 3
Berdasarkan pengamatan anda terhadap grafik fungsi kuadrat[br]yang muncul pada media di atas, bagaimana bentuk grafik fungsi kuadrat jika[br]b=0?
Soal 4
Berdasarkan pengamatan anda terhadap grafik fungsi kuadrat[br]yang muncul pada media di atas, bagaimana bentuk grafik fungsi kuadrat jika[br]c>0?
Soal 5
Berdasarkan pengamatan anda terhadap grafik fungsi kuadrat[br]yang muncul pada media di atas, bagaimana bentuk grafik fungsi kuadrat jika[br]c=0?
Soal 1
Apa yang dapat Anda simpulkan tentang bentuk umum persamaan kuadrat. Bagaimana nilai koefisiennya memengaruhi grafik?
Soal 2
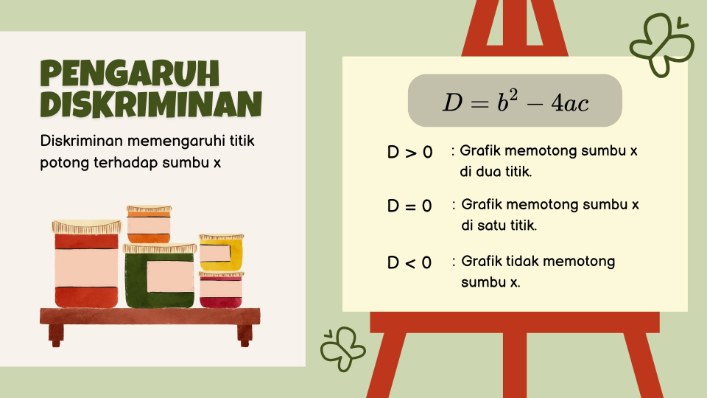
Apa yang dapat anda simpulkan terkait bentuk grafik berdasarkan nilai diskriminan?[br]
Soal 3
Apa yang dapat anda simpulkan terkait titik puncak dalam grafik fungsi kuadrat?
Evaluasi
