PERSAMAAN GARIS LURUS

Atana Sa'adah, Mar 11, 2025

• Kemiringan • Persamaan garis lurus • Titik potong garis • Kedudukan dua garis

Table of Contents

  1. Gradien (Kemiringan)
    1. Gradien part 1
    2. Gradien part 2
  2. Persamaan Garis Lurus
    1. Menentukan Persamaan Garis Lurus
    2. PERSAMAAN GARIS LURUS
    3. GRAFIK PERSAMAAN GARIS LURUS
  3. Titik Potong Garis
    1. Titik Potong Garis
  4. Kedudukan Dua Garis
    1. Kedudukan garis pada bidang koordinat kartesius

1.

Gradien (Kemiringan)

  • 1. Gradien part 1
  • 2. Gradien part 2

1.1.

Gradien part 1

Pertanyaan Pemantik
[*]1. Pernahkah kamu berjalan naik ke bukit atau turun dari tangga? Menurutmu, apa yang membuat suatu jalan terasa lebih curam atau lebih landai?[br][br][/*][*]2. Ketika kamu menggambar garis lurus di bidang kartesius, bagaimana kamu tahu apakah garis itu naik, turun, atau datar?[br][/*][*][br]3. Jika kamu sedang naik sepeda di jalan yang miring, lebih mudah ke atas atau ke bawah? Bagaimana kamu tahu arah kemiringannya?[/*][*][br]4. Bagaimana kamu bisa membedakan garis yang lebih curam dari garis lainnya hanya dengan melihatnya? Apakah kamu bisa mengukurnya dengan angka?[br][/*][*][br]5. Menurutmu, adakah cara matematika untuk mengukur “kemiringan” garis secara tepat, bukan hanya dengan mata?[br][/*]
Pengertian Gradien
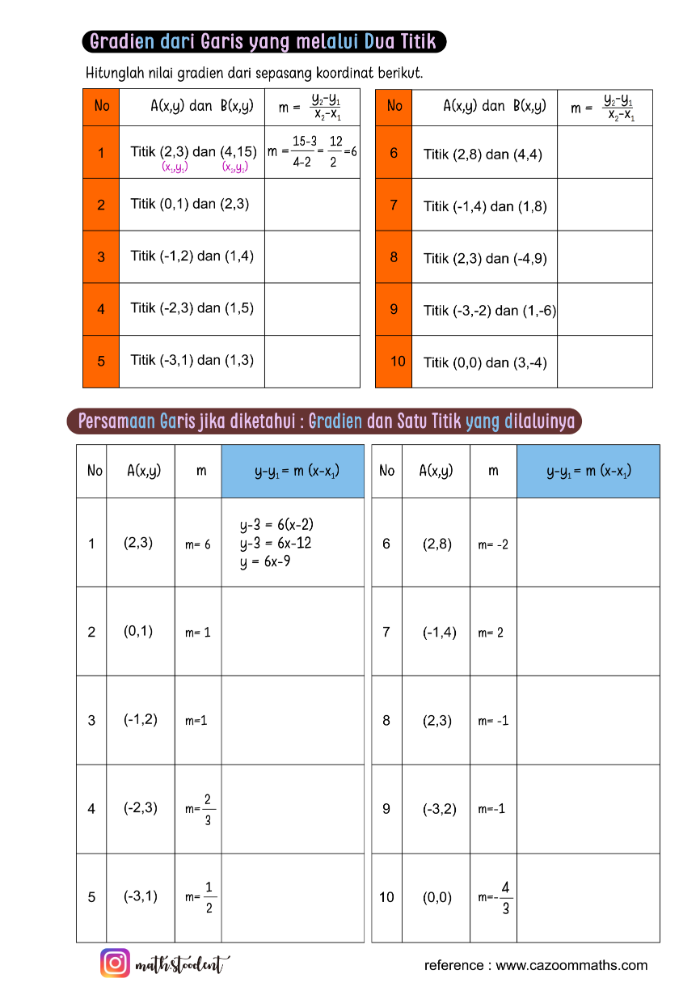
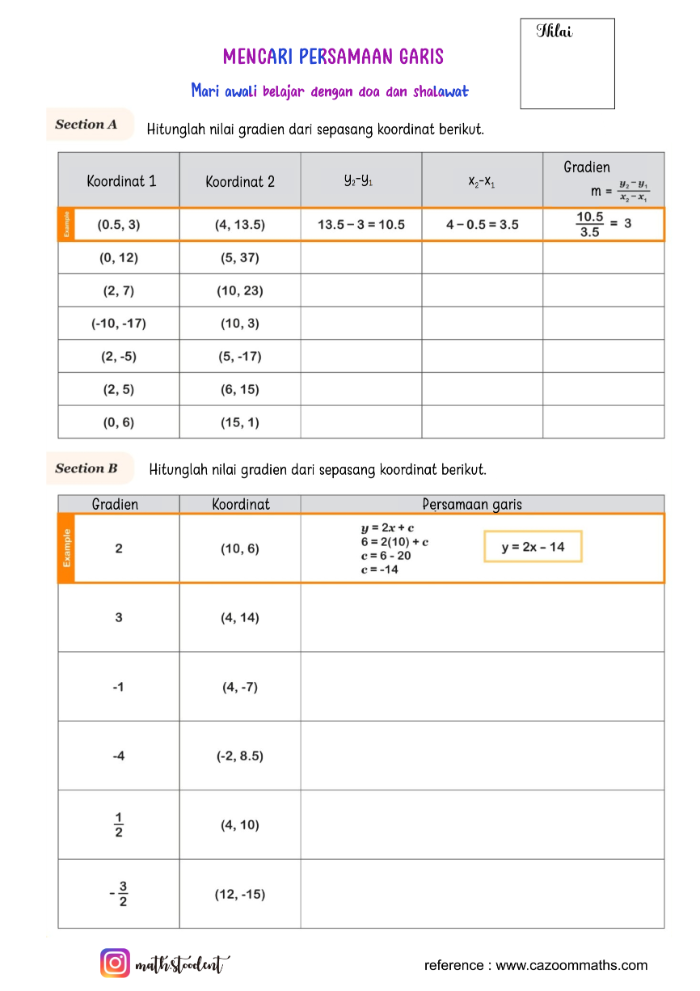
Definisi dari gradien adalah “Nilai kemiringan / kecondongan suatu garis yang membandingkan antara komponen Y (ordinat) dengan komponen X (absis).” Gradien akan menentukan seberapa jauh kemiringan yang terjadi pada suatu garis dalam koordinat Cartesius. Kemiringan atau gradien bisa miring ke kanan, ke kiri, curam, ataupun landai. Nilai dari gradien tergantung dari nilai komponen X dan komponen Y-nya.
Sifat-sifat Gradien
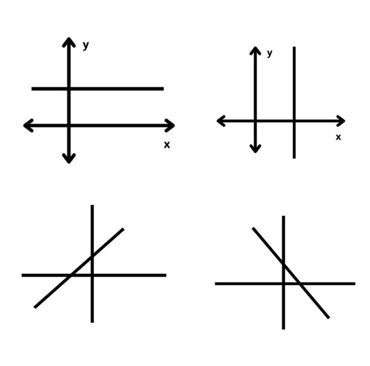
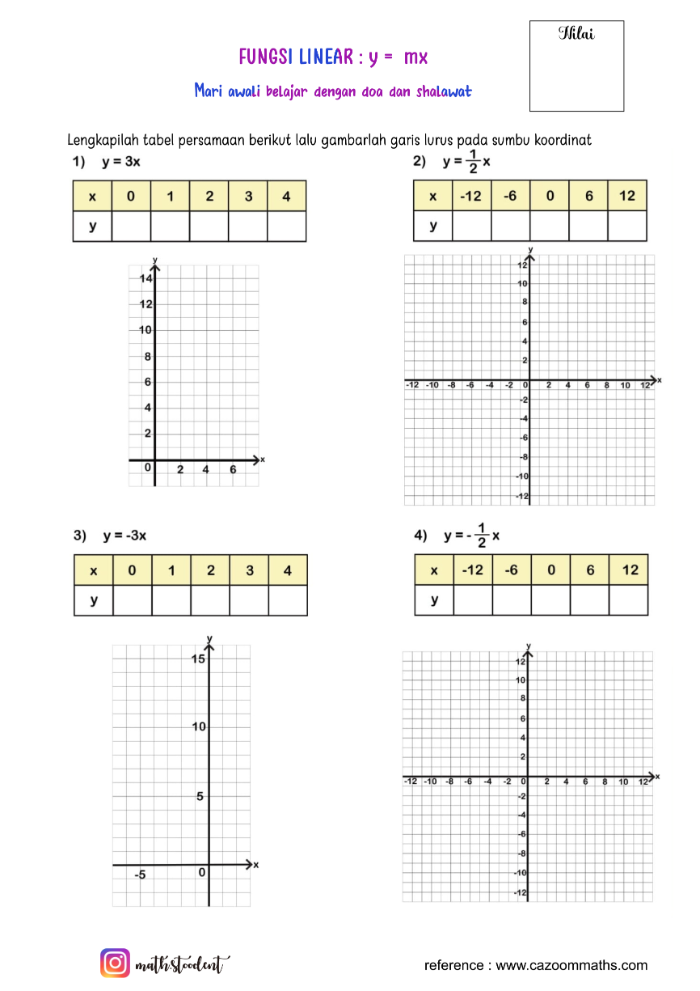
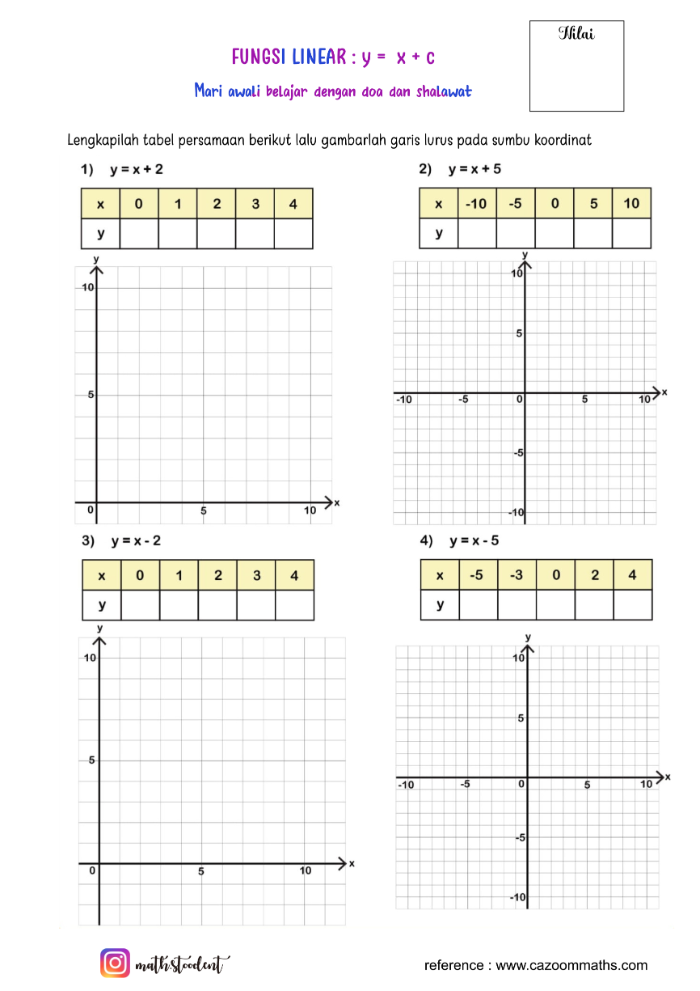
[size=100]1. Apabila suatu garis sejajar dengan sumbu x, maka nilai gradiennya adalah nol (0).[br]2. Apabila suatu garis sejajar dengan sumbu y, maka garis tersebut tidak memiliki gradien.[br]3. Apabila suatu garis miring ke kanan, maka gradiennya bernilai positif.[br]4. Apabila suatu garis miring ke kiri, maka gradiennya bernilai negatif.[/size]
Siswa dapat menentukan garis agar sesuai dengan gradien yang diminta
Siswa dapat menentukan gradien suatu garis
Siswa dapat menentukan gradien suatu garis
Siswa dapat menentukan gradien suatu garis
Siswa dapat menentukan gradien suatu garis
Siswa dapat menentukan gradien garis (m) pada persamaan garis y=mx+c dan memahami gambar grafiknya
Siswa dapat memahami gradien (m) yang ditunjukkan pada bentuk umum y=mx+c dari dua garis sejajar
Siswa dapat menentukan gradien suatu garis
Materi lengkap dari defantri.com
– Alex CHIK, NRICH Maths project, Ooi Soo Huat, Lee W Fisher, Tim Brzezinski, Jennifer Silverman, Atana Sa'adah, intan

1.2.

–

2.

Persamaan Garis Lurus

  • 1. Menentukan Persamaan Garis Lurus
  • 2. PERSAMAAN GARIS LURUS
  • 3. GRAFIK PERSAMAAN GARIS LURUS

2.1.

Menentukan Persamaan Garis Lurus

Pertanyaan Pemantik
[*]1. Kalau kamu berjalan dengan kecepatan tetap, lalu mencatat jarakmu dari waktu ke waktu, menurutmu apakah jarak dan waktu punya hubungan yang bisa diprediksi? Bisa nggak kita tulis hubungan itu dalam bentuk rumus?[br][br][/*][*]2. Jika kamu tahu bahwa setiap 1 jam kamu bisa membaca 20 halaman buku, bagaimana cara mengetahui berapa halaman yang akan selesai kamu baca dalam 5 jam? Bisa nggak kita buat rumus untuk itu?[br][br][/*][*]3. Apa yang terjadi dengan tinggi air dalam ember jika air terus ditambah 2 liter setiap menit? Apakah perubahan tingginya bisa kamu gambarkan dalam bentuk garis?[br][br][/*][*]4. Pernahkah kamu melihat grafik lurus di kertas milimeter atau grafik harga barang? Bagaimana kamu tahu rumus dari garis itu?[br][br][/*][*]5. Kalau kamu tahu bahwa harga 1 pensil adalah Rp2.000, dan kamu ingin beli pensil lebih dari satu, bagaimana kamu membuat rumus total harga berdasarkan jumlah pensil?[br][br][/*][*]6. Menurutmu, apakah semua garis bisa ditulis dalam bentuk persamaan? Bagaimana caranya kita bisa mengetahui bentuk garis hanya dari persamaannya?[br][/*]
Persamaan Umum Garis Lurus yang Melalui Dua Titik
Secara umum persamaan garis lurus yang melalui dua titik berbeda [math]\left(x_1,y_1\right)[/math] dan [math]\left(x_2,y_2\right)[/math] yaitu [math]\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}[/math][br][br]Berikut ini merupakan contoh menentukan persamaan dari suatu garis lurus[br]*gunakan tombol NEXT and BACK untuk melihat urutan langkah-langkahnya
Rumus Khusus untuk Menentukan Persamaan Garis Lurus
Pada kasus khusus andaikan garis lurus tersebut diketahui memotong sumbu x dan sumbu y masing-masing di titik yang berbeda. [br]Misalkan garis lurus memotong sumbu x di (a,0) dan memotong sumbu y di (0,b).[br]Maka menggunakan rumus persamaan umum garis lurus diperoleh [math]\frac{y-0}{b-0}=\frac{x-a}{0-a}[/math][br]dapat disederhanakan menjadi [math]\frac{y}{b}=\frac{x}{-a}+1[/math][br]atau dapat ditulis sebagai [math]\frac{x}{a}+\frac{y}{b}=1[/math][br][br]Sehingga secara khusus, bila diketahui titik potong garis dengan sumbu x adalah (a,0) dan titik potong sumbu y adalah (0,b), maka persamaan garisnya dapat disusun dengan lebih sederhana menggunakan rumusan [math]\frac{x}{a}+\frac{y}{b}=1[/math][br][br]Simak contoh berikut ini untuk lebih jelasnya
LATIHAN MANDIRI
Setelah mencermati contoh di atas, silahkan gunakan kalian berlatih secara mandiri melalui aktivitas di bawah ini.[br]Tuliskan persamaan garis tampil pada kolom [b]PERSAMAAN GARIS[/b][br]Gunakan tombol [b]PERIKSA[/b] untuk memeriksa jawaban.[br]Klik [b]SOAL BARU[/b] untuk mencoba soal lain.[br]Raih [b]SKOR[/b] mu setinggi mungkin !
Siswa dapat menentukan persamaan garis lurus dari suatu grafik garis lurus
Siswa dapat menentukan grafik garis lurus jika diketahui persamaan garisnya
SIswa dapat menggambarkan persamaan garis ke grafik
Siswa dapat memahami konsep persamaan garis lurus
SIswa dapat menggambarkan persamaan garis ke grafik dengan mensubstitusikan nilai x untuk memperoleh y menjadi titik (x,y)
SIswa dapat menggambarkan persamaan garis ke grafik dengan mensubstitusikan nilai x untuk memperoleh y menjadi titik (x,y)
SIswa dapat menggambarkan persamaan garis ke grafik dengan mensubstitusikan nilai x untuk memperoleh y menjadi titik (x,y)
Siswa dapat menentukan persamaan garis jika diketahui tabel nilai (x,y) dan gambar grafik
Siswa dapat menggambarkan garis pada diagram kartesius jika diketahui persamaan garis lurusnya. Bentuk umum yang digunakan yakni y=mx+c. Gradien ditunjukkan oleh m dan titik potong garis dengan sumbu y ditunjukkan oleh c
Siswa dapat menggambarkan garis pada diagram kartesius jika diketahui persamaan garis lurusnya. Bentuk umum yang digunakan yakni y=mx+c. Gradien ditunjukkan oleh m dan titik potong garis dengan sumbu y ditunjukkan oleh c
– Anthony Dove, Tim Brzezinski, Lee W Fisher, Edward Knote, chris cambré, Virtual Mathematics Laboratory, Atana Sa'adah, Denny Pritianto

2.2.

–

2.3.

–

3.

Titik Potong Garis

  • 1. Titik Potong Garis

3.1.

Titik Potong Garis

[color=#e06666][i][size=85]Mari awali belajar dengan doa dan shalawat[/size][/i][/color]
Pertanyaan Pemantik
[list=1][*]Saat kamu menggambar garis di bidang koordinat, apakah kamu memperhatikan di mana garis itu menyentuh sumbu X dan sumbu Y? Kira-kira apa artinya titik itu?[br][br][/*][*]Jika kamu menyeberang jalan lurus dari satu sisi trotoar ke sisi lain, kira-kira di titik mana kamu “memotong” jalur mobil (sumbu jalan)? Bisa nggak kita analogikan itu dengan garis memotong sumbu?[br][br][/*][*]Kalau kamu punya persamaan garis, apakah kamu bisa langsung tahu di mana garis itu menyentuh sumbu X dan Y tanpa menggambarnya?[br][br][/*][br][*]Mengapa titik potong dengan sumbu Y penting saat membuat grafik? Apakah itu bisa memberi tahu kita dari mana garis ‘berawal’?[br][br][/*][*]Kalau dua orang berjalan dari arah berbeda dan jalur mereka saling berpotongan, apa yang bisa kamu katakan tentang titik pertemuan mereka? Bagaimana kamu bisa mengetahui titik potong dua garis?[br][/*][br][*]Pernahkah kamu berpikir, dalam kehidupan nyata, apa artinya ‘titik pertemuan’ antara dua hal? Bisa nggak kita gambarkan pertemuan itu dalam grafik?[br][/*][/list]
Menentukan koordinat titik potong
Siswa dapat memahami titik potong antara dua garis
Siswa dapat menentukan titik potong dua garis
– Nabila Shofiyatus Sholiha nabilashofiyatus.2023, Lutfi Adnan Muzamil, Atana Sa'adah

4.

Kedudukan Dua Garis

  • 1. Kedudukan garis pada bidang koordinat kartesius

4.1.

Kedudukan garis pada bidang koordinat kartesius

[color=#e06666][i][size=85]Mari awali belajar dengan doa dan shalawat[/size][/i][/color]
Pertanyaan Pemantik
[*]1. Pernahkah kamu melihat dua rel kereta api? Mengapa rel itu tidak pernah bersinggungan? Apa yang terjadi jika mereka tidak sejajar?[br][/*][*][br]2. Kalau dua orang berjalan dari arah berbeda dan jalurnya saling bertemu di satu titik, menurutmu apa yang bisa dikatakan tentang arah mereka?[br][br][/*][*]3. Apa bedanya dua garis yang sejajar dengan dua garis yang tegak lurus? Kira-kira mana yang lebih sering kamu lihat dalam bangunan atau jalanan?[br][br][/*][*]4. Pernahkah kamu melihat garis-garis di zebra cross? Apakah menurutmu itu sejajar, tegak lurus, atau berpotongan?[br][br][/*][*]5. Kalau kamu menggambar dua garis lurus dan menemukan bahwa mereka saling berpotongan di satu titik, apakah semua garis yang berpotongan pasti tegak lurus?[br][br][/*][*]6. Bisakah dua garis saling menindih (berada tepat di atas satu sama lain)? Apa nama posisi itu dalam matematika?[br][/*]
Kedudukan Garis
[list][*][color=#0000ff][b]Garis sejajar adalah[/b] suatu kedudukan dua garis pada bidang datar yang tidak mempunyai titik potong walaupun kedua garis diperpanjang.[/color][/*][*][color=#0000ff][b]Garis berpotongan adalah[/b] kedudukan dua garis yang mempunyai titik potong karena kedua garis saling bertemu.[/color][/*][*][color=#0000ff][b]Garis tegak lurus adalah[/b] kedudukan garis yang berpotongan dan pada titik potongnya terbentuk sudut siku-siku (90°)[/color][/*][/list]
Gambar Garis Sejajar, Garis Berpotongan, dan Garis Tegak Lurus
[b][color=#741B47]Berikut contoh kedudukan garis pada bidang koordinat kartesius[br][/color][br][/b]
Siswa dapat memahami kedudukan dua garis berpotongan pada koordinat kartesius
Siswa dapat memahami kedudukan dua garis saling berpotongan tegak lurus pada koordinat kartesius
Siswa dapat memahami kedudukan dua garis sejajar pada koordinat kartesius
Evaluasi
– Encep Mulyana, Atana Sa'adah, Fara Anggraeni

Information