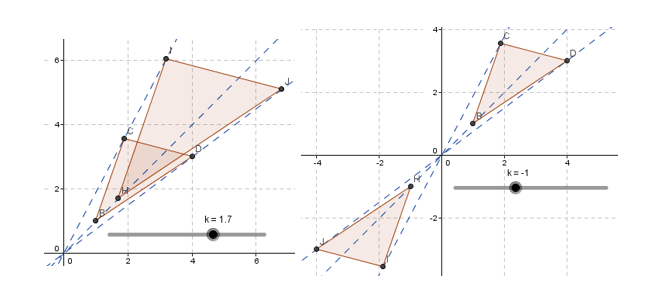
[br][br][b][i]Навчальне дослідження 1[/i][/b][b].[/b][br]Змінюючи значення коефіцієнта [b]k[/b] і[br]положення точок, спостерігайте за змінами трикутників. Зверніть окрему увагу на[br]ситуацію при [b]k[/b]=0, [b]k[/b]=1,[b] k[/b][b]<[/b]0.[br]Зробіть висновки щодо зв’язку між вихідними і побудованими трикутниками. [br][br][br][b][i]Навчальне дослідження 2[/i][/b][b].[/b] Змініть формули в комірках з[br]координатами точок так, щоб побудувати симетричні трикутники відносно осі Ох та[br]осі Оу.[br][br][br][b][i]Навчальне дослідження 3[/i][/b][b]. [/b]Побудуйте гомотетичні[br]трикутники відносно довільної точки [b]Х.[/b][br][br][br]

[br][br][i]Навчальне дослідження 1:[/i][br][br] Два даних трикутника є гомотетичними. При[br]зміні положення вершин вихідного трикутника вершини похідного трикутника рухаються[br]відповідно.[br][br][br]При [b]k[/b]=1 трикутники збігаються. При [b]k[/b]=0 похідний трикутник вироджується в[br]точку, що лежить на початку координат. При [b]k[/b]<0[br]положення трикутників віддзеркалюється відносно початку координат.[br][br][br]При зміні[br]коефіцієнта k можна помітити, що вершини похідного трикутника рухаються по[br]прямих, які проходять через протилежні вершини гомотетичних трикутників і[br]перетинаються на початку координат.[br][br][br]