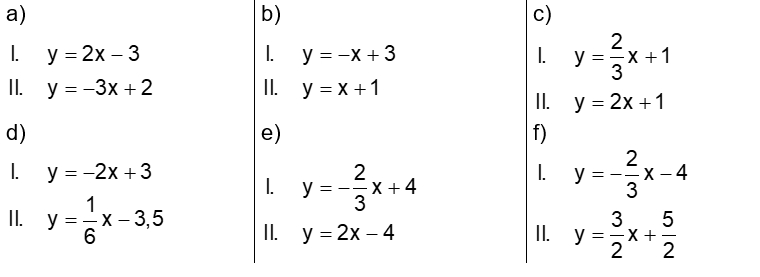Grafische Lösung
Arbeitsblatt zur grafischen Lösung von Linearen Gleichungssystemen
Ihr plant eine Klassenfahrt. Folgende beiden Angebote von zwei Busunternehmen liegen euch vor.
Beschreibe die Unterschiede der beiden Angebote in eigenen Worten.
Unter welchen Gesichtspunkten würdest du dich für welches der Angebote entscheiden?
Wie lauten die beiden Angebote als Gleichung ausgedrückt?
y € steht für den Gesamtpreis bei x km + Grundpreis t.[br][br][i]Erinnerung: y = mx + t[/i]
[u][b]Bei welcher Strecke zahlt man bei beiden Unternehmen gleich viel?[br][br][/b][/u]... heißt mathematisch: [b][u]Wann sind beide Gleichungen gleichzeitig erfüllt?[/u][/b][br]=> Zwei Gleichungen ergeben ein Lineares Gleichungssystem (LGS) und werden durch "∧" (und zugleich) verknüpft.[br][br][br]Um das herauszufinden, zeichne die beiden Gleichungen der Angebote in das Koordinatensystem ein![br]Du kannst die Punkte bewegen und so die Graphen einstellen.
Wie erkenne ich grafisch im KOSY, wann beide Gleichungen erfüllt sind bzw. wann beide Anbieter gleich teuer sind?
Bei welcher Strecke x km zahle ich bei beiden Anbietern gleich viel y €?
Lösung zum Arbeitsblatt
Aufgabe: Bestimme die Lösungsmenge der Gleichungssystem grafisch.
