Mi primer libro GEOGEBRA
Ejercicios de introducción de la especialización TEDIEM, FES Acatlan, UNAM
Table of Contents
- Geogebra Geometría
- Construcción básica de un paralelogramo
- Construcción básica de un cuadrado
- Circunferencia circunscrita a un triángulo
- Funciones y Cálculo
- Ecuación ordenada al origen de la recta
- Construcción de curvas sinuosidades
- Interpretación geométrica de la derivada
- Análisis de un polinomio
- Traslaciones, rotaciones y reflexiones
- Simetria de una imagen.
- Distorsión y reflexión de una imagen
- Traslación de una imagen
- Rotación de un objeto a un ángulo dado.
- Video de introducción
- Sitio Web de Transformaciones
- Texto estático y dinámico
- Escena 1: Cálculo de la pendiente de una recta.
- Ejemplo de aritmética modular
- Interpretación geométrica de la formula del binomio
- Herramientas personalizadas
- Interpretación geométrica del Teorema de Pitágoras
- La espiral de Fibonacci
- La recta Euler
- Condicionales y listas
- Aritmética de números enteros.
- El Triángulo de Sierpinski.
- Ejemplos de Secuencias.
- Multiplicación de los números naturales
- Hojas de cálculo y estadística básica
- Análisis de patrones numéricos para construir polinomios.
- Modelo de regresión lineal.
- Vista CAS y sus comandos
- Intersección de Polinomios
- Solución de sistemas de ecuaciones
- Operaciones con matrices y vectores
Construcción básica de un paralelogramo
[b]Instrucciones.[br][/b][br]1. [icon]/images/ggb/toolbar/mode_join.png[/icon] Seleccione la herramienta [b]Recta[/b] que pasa por dos puntos, dando dos clics sucesivos en el espacio de trabajo, los cuales se denominarán A y B.[br][br]2. [icon]/images/ggb/toolbar/mode_complexnumber.png[/icon] Seleccione la herramienta [b][i]Punto[/i][/b], dando clic arriba de la recta, el cual se denominará C.[br][br]3. [icon]/images/ggb/toolbar/mode_join.png[/icon] Seleccione la herramienta [b]Recta[/b] que pasa por dos puntos, dando clic en los puntos B y C.[br][br]4. [icon]/images/ggb/toolbar/mode_parallel.png[/icon] Seleccione la herramienta [i]Paralela[/i], dando clic en la recta que pasa por los puntos A y B, después de clic en el punto C.[br][br]5. [icon]/images/ggb/toolbar/mode_parallel.png[/icon] Seleccione la herramienta [i][b]Paralela[/b][/i], dando clic en la recta que pasa por los puntos B y C, después de clic en el punto A.[br][br]6. [icon]/images/ggb/toolbar/mode_intersect.png[/icon] Seleccione la herramienta [b][i]Intersección[/i][/b], dando clic en el punto de intersección de estas rectas paralelas, el cual se denominará punto D.[br][br]7. [icon]/images/ggb/toolbar/mode_polygon.png[/icon] Seleccione la herramienta [b][i]Polígono[/i][/b], dando clic en los cuatro puntos.[br][br][b][i][u]Nota[/u]:[/i][/b] No olvide cerrar el polígono haciendo clic en el mismo vértice en el que inició su creación.[br]
Ecuación ordenada al origen de la recta
¿Las funciones lineales son de primer grado?
¿Que es la ordenada al origen?
Problema de aplicación de función lineal
[b]Ejemplo[/b][b]. [/b]El alquiler diario de un automóvil, es $300 más $10 por cada kilómetro recorrido.[br]a) ¿Cuántos kilómetros recorrió si pago $530?[br]b) ¿Si recorrió 35 km cuánto pago?[br]
Simetria de una imagen.
Simetria de una imagen.
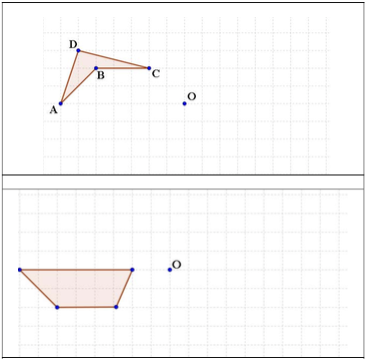
[b]Ejercicio.[/b] Dibuja el simétrico de cada figura aplicando la simetría central de centro el punto dado.[br]
Ejercicio. Dibuja el simétrico de cada figura aplicando la simetría central de centro en el punto dado.
Escena 1: Cálculo de la pendiente de una recta.
Escena 1: Cálculo de la pendiente de una recta.
Texto explicativo
Para desarrollar esta applet, se utilizó texto estático y dinámico, se ingresaron dos puntos para trazar una recta, con los valores de estos puntos, se trazaron los incrementos, de: [b]Delta-x[/b] y [b]Delta-y[/b], se calculan estos valores paso por paso para que esta escena sea mas ilustrativa, también se le agregaron colores a textos estáticos y dinámicos.[br][br]Por otro lado se observa gráficamente que la pendiente de la recta, puede ser positiva o negativa,
Interpretación geométrica del Teorema de Pitágoras
Interpretación geométrica del Teorema de Pitágoras
Aritmética de números enteros.
Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero [br](1, 2, 3, ...), los opuestos de los números naturales (..., −3, −2, −1) y al cero, 0.[br][br]El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}, que proviene del alemán [i]Zahlen[/i] («números», pronunciado [ˈtsaːlən]).[br][br]En la matemática moderna el conjunto de los números enteros al abarcar todos los enteros tanto negativos como positivos, representándolos en una recta numérica "llega" hasta el infinito hacia ambos lados, en rigor no existe un comienzo ni un final. La situación no cambiaría en el caso de usar el cero como "origen" para su localización.
Análisis de patrones numéricos para construir polinomios.
En esta escena se observa que en la hoja de cálculo, en la columna A se introdujeron valores del 1 al 10, después en la columna B se introdujeron formulas, por ejemplo: en la celda B1 la formula es: = 6 A1[sup]2[/sup], en la celda B2 la formula es: = 6 A2[sup]2[/sup] y así sucesivamente, se arrastro dicha celda para obtener los demás valores hasta B10.[br][br]Después se selecciona la columna A y B hasta la fila 10, para crear la lista de puntos, que se observan en la vista gráfica: puntos: A, B, C, D, E, F, G, H, I, J.[br][br]También se introdujo en la barra de entrada la función: p(x) = a x[sup]n[/sup].[sup][br][/sup][br]En la vista gráfica se observa que al mover los deslizadores a y n, a los valores de a = 6 y n = 2, la función: p(x) = 6 x[sup]2[/sup], pasa por los puntos: A, B, C, D, E, F, G, H, I, J.[br]
Intersección de Polinomios
En esta escena, se observa la intersección de dos funciones f(x) y g(x), la función f(x) es una parábola y la función g(x) es una recta, también se observa que al restar las funciones f(x) y g(x) se obtiene la función h(x), que también es una parábola, que al factorizarse esta ultima: h(x) se obtienen los ceros de la función.[br][br]Por otro lado, se observan las intersecciones de las funciones f(x) y g(x). Este tipo de análisis es importante para distinguir una parábola de una recta.