Trigonometría
Trigonometría
Table of Contents
- Definiciones
- Definición de senos, cosenos y tangentes para cualquier ángulo
- Relaciones
- Relación de razones trigonométricas entre ángulos de distintos cuadrantes
- Resolución de triángulos
- Teorema del coseno
- Teorema del seno
- Resolución de triángulos no rectángulos (I)
- Resolución de triángulos no rectángulos (II)
- Resolución de triángulos no rectángulos (III)
- Resolución de triángulos no rectángulos (y IV)
- Ecuaciones trigonométricas
- Ecuación trigonométrica seno
- Ecuación trigonométrica coseno
- Ecuación trigonométrica tangente
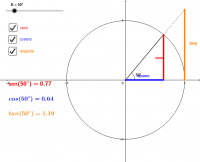
Definición de senos, cosenos y tangentes para cualquier ángulo
El deslizador cambia el ángulo. Para cada ángulo se ve representado el seno (rojo), el coseno (azul) y la tangente (naranja) El texto muestra el valor de cada razón trigonométrica.
Relación de razones trigonométricas entre ángulos de distintos cuadrantes
El deslizador cambia el ángulo. El activar cada una de las casillas de verificación se ve:[br][list][*]Para el primer caso el ángulo del primer cuadrante y su correspondiente ángulo suplementario.[/*][*]Para el segundo caso el ángulo del primer cuadrante y otro que difiere de él 180º.[/*][*]Para el tercer caso el ángulo del primer cuadrante y su opuesto.[/*][*]Para el cuarto caso el ángulo del primer cuadrante y su complementario.[/*][/list]En cada uno de los tres primeros casos se muestra el seno del ángulo y de su correspondiente (en rojo), que tienen la misma longitud y que pueden tener el mismo signo (orientados a la parte positiva del eje y) o signo contrario; y el coseno del ángulo y de su correspondiente (en azul) que vuelven a tener la misma longitud y que pueden tener el mismo signo (orientados a la parte positiva del eje x) o el signo contrario.[br]Para el último caso, se muestran los segmentos que tienen la misma longitud del mismo color, observando que el seno de un ángulo corresponde con el coseno del otro ángulo y viceversa.
Teorema del coseno
En la presente actividad observamos la demostración del teorema del coseno para todas las posibilidades. Para ello, basta con mover el punto A y observar las distintas opciones.
Ecuación trigonométrica seno
Se resuelve la ecuación trigonométrica [math]sen\left(x\right)=t[/math]. El deslizador cambia el valor de t. Se ve la solución de cada ecuación gráficamente, mostrando los ángulos que hacen que el seno tome ese valor.