Calcolatrice CAS GeoGebra - Tutorial
Ecco la [url=https://www.geogebra.org/cas]Calcolatrice CAS GeoGebra[/url]! Con questo tutorial imparerai a tracciare grafici di funzioni, calcolare derivate e integrali, risolvere equazioni e molto altro ancora.
Table of Contents
- Primi passi
- App GeoGebra a confronto
- Introduzione
- Esploriamo l'app
- Operazioni di base
- Definire funzioni
- Termini e variabili
- Risolvere equazioni e disequazioni
- Risolvere sistemi di equazioni
- Calcolare i limiti delle funzioni
- Calcolare le derivate
- Integrali definiti e indefiniti
- Operazioni avanzate
- Funzioni razionali
- Volume di rotazione
- Studio di funzione
- Funzioni polinomiali di 4° grado
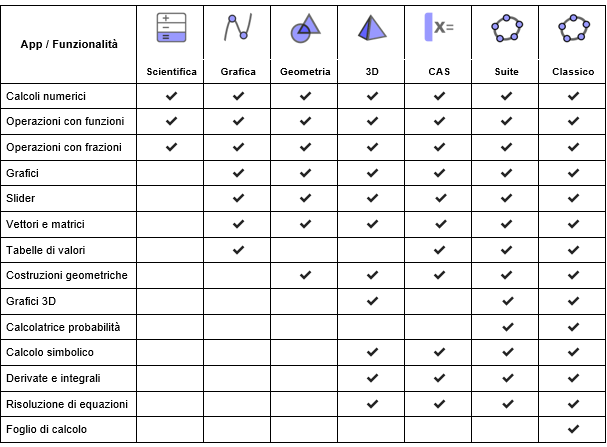
App GeoGebra a confronto
Con le app [i]GeoGebra [/i]è possibile esplorare le funzioni, la geometria, l'algebra, la statistica e lo spazio 3D in un modo nuovo e interattivo.[br][list][*][url=http://www.geogebra.org/scientific]Calcolatrice scientifica[/url][br][/*][*][url=https://www.geogebra.org/graphing]Calcolatrice grafica[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometria[/url][br][/*][*][url=https://www.geogebra.org/calculator]Suite calcolatrici[/url][/*][*][url=https://www.geogebra.org/cas]Calcolatrice CAS[/url][br][/*][*][url=https://www.geogebra.org/3d]Calcolatrice 3D[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]L'app giusta per voi è quella che soddisfa le vostre necessità, ed è totalmente compatibile con le restrizioni imposte localmente per gli esami e i test scolastici. La tabella che segue vi offre una panoramica delle funzionalità disponibili per ogni app.
Utilizzare GeoGebra agli esami
Siamo totalmente convinti che per gli studenti sia un beneficio utilizzare esattamente la stessa app [i]GeoGebra [/i]in classe, per lo studio a casa e durante gli esami. In questo modo saranno in grado di esercitarsi e imparare bene il funzionamento dell'app, e quindi sfruttare la tecnologia nel modo migliore in qualsiasi situazione. Ecco perché abbiamo creato la [url=https://www.geogebra.org/m/hvtasyxw]modalità Esame di GeoGebra[/url] e l'abbiamo inserita in ogni app. La [i]modalità Esame[/i] blocca il dispositivo mobile in modo tale che gli studenti non possano comunicare tra loro o utilizzare qualsiasi altra app durante un esame. Questa funzionalità è stata testata sul campo ed approvata da vari ministeri dell'istruzione in varie regioni del mondo. Scopri come [url=https://www.geogebra.org/m/hvtasyxw]utilizzare GeoGebra negli esami[/url].[br][br]Per ulteriori informazioni o domande relative all'utilizzo delle [i]app GeoGebra[/i] e alla [i]modalità Esame[/i], non esitate a contattarci all'indirizzo [url=mailto:support@geogebra.org]support@geogebra.org[/url]
Definire funzioni
Attività
Definisci una funzione e visualizzane il grafico nella [i]vista Grafici[/i], quindi calcola alcuni dei valori assunti dalla funzione (immagini e controimmagini).
Esplora la costruzione...
Istruzioni
[table][tr][td]1.[/td][td]Inserisci la funzione [math]f\left(x\right)=x^3+6x^2+6x-4[/math] nella [i]barra di inserimento[/i] e premi [i]Invio[/i].[/td][/tr][tr][td][/td][td][b][/b][b]Nota:[/b] Il grafico di [i]f(x) [/i]viene visualizzato in tempo reale nella [i]vista Grafici. [/i][i][/i][/td][/tr][tr][td]2.[/td][td]Calcola gli zeri di [i]f(x)[/i] inserendo il comando [math]Risolvi\left(f=0\right)[/math] nella [i]barra di inserimento[/i] e premendo [i]Invio[/i]. [br][/td][/tr][tr][td]3.[/td][td]Calcola i valori assunti dalla funzione quando [i]x = -5[/i], [i]x = 0 [/i]e [i]x = 2.15[/i] inserendo [math]f\left(\left\{-5,0,2.15\right\}\right)[/math] nella [i]barra di inserimento[/i] e premendo [i]Invio[/i].[/td][/tr][tr][td]4.[/td][td]Calcola i valori di [i]x[/i] tali che [i]f(x) = 4, [/i]inserendo il comando [math]Risolvi\left(f=4\right)[/math] nella [i]barra di inserimento[/i] e premendo [i]Invio[/i].[/td][/tr][/table][b]Nota:[/b] Puoi passare dai risultati in forma [img]https://wiki.geogebra.org/uploads/thumb/6/66/Numeric_toggle_button.png/24px-Numeric_toggle_button.png[/img] decimale approssimata alla forma [img]https://wiki.geogebra.org/uploads/thumb/8/8b/Symbolic_toggle_button.png/24px-Symbolic_toggle_button.png[/img] esatta, selezionando il corrispondente pulsante.
Ora prova tu...
Funzioni razionali
Attività
Data la funzione [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math].[br][list=1][*]Traccia il grafico di [i]f[/i]([i]x[/i]).[/*][*]Determina il dominio [i]D[/i] e gli zeri di [i]f[/i]([i]x[/i]).[/*][*]Studia il comportamento di [i]f[/i]([i]x[/i]) agli estremi del dominio [i]D[/i].[/*][/list]
Esplora la costruzione...
Istruzioni
[table][tr][td]1.[/td][td]Definisci [i]f[/i]([i]x[/i]) inserendo [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math] nella [i]barra di inserimento[/i], quindi premi [i]Invio [/i]per confermare. [/td][/tr][tr][td][/td][td][b]Nota:[/b] La [i]Calcolatrice CAS[/i] [i]GeoGebra[/i] semplifica automaticamente l'equazione di [i]f[/i]([i]x[/i]).[/td][/tr][tr][td]2.[/td][td]Usa il comando [math]Radice(f)[/math] per determinare gli zeri di [i]f[/i]([i]x[/i]).[br][/td][/tr][tr][td][/td][td][b]Nota: [/b]In alternativa, puoi utilizzare il comando [math]Risolvi(f=0)[/math] per determinare gli zeri della funzione.[/td][/tr][tr][td]3.[/td][td]Per determinare il dominio di [i]f[/i]([i]x[/i]), calcola gli zeri del denominatore di [i]f[/i]([i]x[/i]) inserendo il comando [math]Radice(Denominatore(f))[/math].[br][/td][/tr][tr][td][/td][td][b]Nota:[/b] Puoi utilizzare anche il comando [math]Risolvi(Denominatore(f)=0)[/math].[/td][/tr][tr][td]4.[/td][td]Poiché la soluzione è [i]-3,[/i] il dominio della funzione è [math]D=\mathbb{R}\backslash\left\{-3\right\}[/math].[/td][/tr][/table]
Ora prova tu...
Istruzioni (continua)
[table][tr][td]5.[/td][td]Utilizza il comando [i]Limite[/i] per studiare il comportamento di [i]f[/i]([i]x[/i]) agli estremi del dominio [i]D[/i]. [/td][/tr][tr][td][/td][td]Inserisci il comando [math]Limite\left(f,-\infty\right)[/math] per studiare il comportamento della funzione nell'intorno di -[i]∞[/i].[/td][/tr][tr][td][/td][td]Inserisci il comando [math]Limite\left(f,\infty\right)[/math] per studiare il comportamento della funzione nell'intorno di +[i]∞[/i].[/td][/tr][tr][td]6.[/td][td]Utilizza i comandi [i]LimiteDestro[/i] e [i]LimiteSinistro[/i] per studiare il comportamento della funzione nell'intorno di [i]x[/i] = [i]-3[/i]. [/td][/tr][tr][td][/td][td]Inserisci il comando [math]LimiteDestro\left(f,-3\right)[/math] nella [i]barra di inserimento[/i].[/td][/tr][tr][td][/td][td]Inserisci il comando [math]LimiteSinistro\left(f,-3\right)[/math] nella [i]barra di inserimento[/i].[/td][/tr][tr][td][br][/td][td][br][/td][/tr][/table]