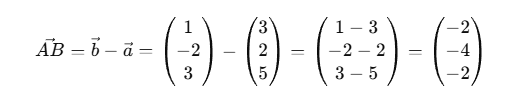
Arbeitsblatt: Vektoren im Raum (Aufgabe1)
Vektoren
Ein [b]Vektor[/b] gibt dir eine genaue [b]Wegbeschreibung[/b]:[br][br]Er zeigt, wie weit du in jede Richtung gehen musst, um von einem Punkt (Bsp. [b]Koordinatenursprung)[/b] zu einem Punkt (Bsp. Punkt [b]P)[/b] zu gelangen. Vektoren, die vom Koordinatenursprung zu einem Punkt zeigen, nennt man [b]Ortsvektoren[/b].[br][br]Das bedeutet:[br][br][b]a[/b] Schritte in [b]x-Richtung[/b][br][br][b]b[/b] Schritte in [b]y-Richtung[/b][br][br][b]c[/b] Schritte in [b]z-Richtung[/b][br][br]Probiere in dem folgenden Applet aus, den Punkt [b]P[/b] mit den Schieberegler zu verschieben und ihn dann in einen [b]Ortsvektor[/b] umzuwandeln!
Vektoren zwischen Punkten
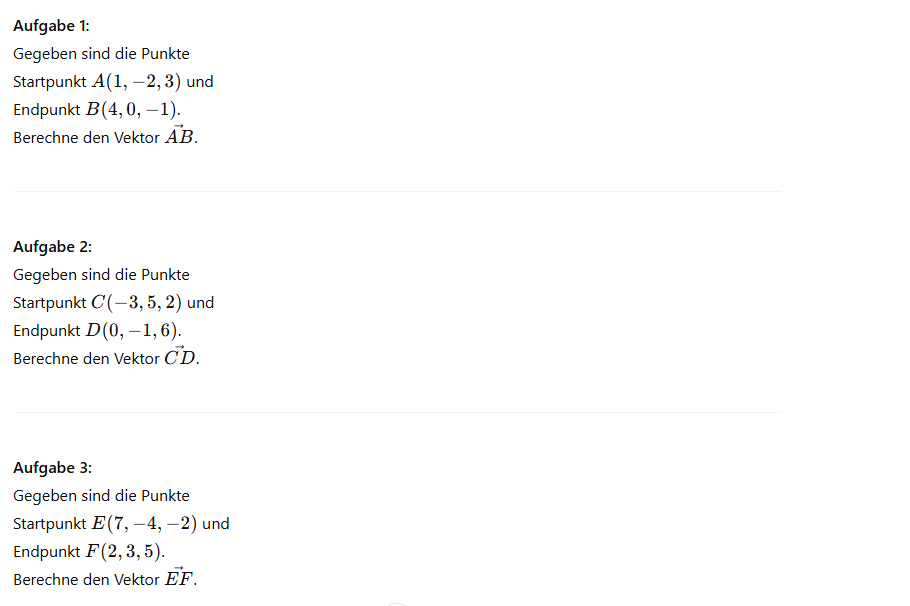
Es ist zudem möglich, Vektoren von einen zu einen anderen Punkt zu berechnen.[br]Jetzt soll herausgefunden werden, wie man [b]vom Punkt A zum Punkt B[/b] gelangt. Gesucht ist also der [b]Vektor von A nach B[/b], der dir genau beschreibt, wie du dich von A aus zu B bewegen musst. [b]Gleiche Vektoren[/b] haben [b]denselben Betrag[/b] (Länge) und [b]dieselbe Richtung[/b]. Das bedeutet, sie verlaufen parallel zueinander und zeigen exakt in dieselbe Richtung – auch wenn sie an verschiedenen Punkten im Raum beginnen.[br][br][b]Vektoren mit gleicher Richtung[/b] haben denselben Richtungsverlauf (d. h. sie sind parallel), können sich aber in ihrer [b]Länge[/b] unterscheiden. [br][br]Probiere auch das im folgenden Applet gerne aus![br][br][br]Einen Vektor vom Anfangspunkt A zum Endpunkt B rechnet man folgendermaßen aus:
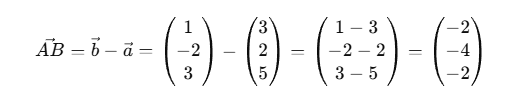
Übung 1:
Entscheide welche Aussagen über die darunter stehenden Vektoren stimmen
Übung 2: Überprüfe deine Ergebnisse mit dem passenden Applet