数学上向量加法的定义如下图所示。

[b]类型[/b][b]Ⅲ[/b]需要三力中有一个力大小和方向确定，另二力方向变化有依据，判断二力大小变化情况。而变化有依据的其中一种情形是夹角定，下面我们就来研究夹角定的情形。（[b]若一个力大小方向确定，另外两个力的夹角确定——用三角形外接圆法）[/b][br]

【例题1】如图所示，柔软轻绳ON的一端O固定，在其上某点M拴一重物，用手拉住绳的另一端N将重物向右上方缓慢拉起。初始时，OM竖直，OM⊥MN。保持OM与MN夹角不变，在OM由竖直被拉到水平的过程中（）[br][br]

由于OM上的张力和MN上的张力始终垂直，而直径所对的圆周角为[math]90^\circ[/math]，因此三个力构成的封闭矢量三角形可以放在一个圆中辅助分析。其中重力处在直径的位置。

【例题2】(2017年全国卷一）如图，柔软轻绳[i]ON[/i]的一端[i]O[/i]固定，其中间某点[i]M[/i]拴一重物，用手拉住绳的另一端[i]N[/i]，初始时，[i]OM[/i]竖直且[i]MN[/i]被拉直，[i]OM[/i]与[i]MN[/i]之间的夹角为[math]\alpha,\left(\alpha>\frac{\pi}{2}\right)[/math]，现将重物向右上方缓慢拉起，并保持夹角不变。在[i]OM[/i]由竖直被拉到水平的过程中[br][br][br]

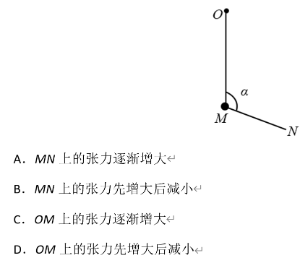
考虑到绳子OM和绳子MN上的张力夹角在首尾相连后是一个大小不变的锐角，而一个弦所对的圆周角也是不变的，因此此题也可以考虑放在圆里面辅助观察。