Summen- und Faktorregel
Laut der Formelsammlung gelten neben der Potenzregel noch folgende Ableitungsregeln:[br][br]1. Faktorregel:[br]Wenn die Funktion g die Ableitung g' hat, dann hat die Funktion f mit f(x) = k ∙ g(x) mit k ϵ R die Ableitung: f'(x) = k ∙ g'(x).[br][br]2. Summenregel:[br]Wenn die Funktion g die Ableitung g' und die Funktion h die Ableitung h' hat, dann hat die Funktion f mit f(x) = g(x) + h(x) die Ableitung: f'(x) = g'(x) + h'(x).[br][br]Im Folgenden sollen Begründungen für diese Regeln gefunden werden.
Darstellung der Funktion f(x)=k ∙ g(x) und der Funktion g(x)=x^n
Anwendung des Applets
Der Punkt P1 ist beweglich.[br]Die Parameter n und k können durch Eingabe verändert werden.
Aufgabe:
Untersuche die Funktionen im Applet und begründe anschließend die Existenz der Faktorregel in mathematischer Fachsprache (verwende Begriffe wie z.B. Tangentensteigung, Steigungsdreieck, ...).
Darstellung der Funktion f(x) = g(x) + h(x) und der Funktionen g(x) = x^s und h(x)=x^r
Anwendung des Applets
Der Punkt P1 ist beweglich.[br]Die Parameter r und s können durch Eingabe verändert werden.[br]Die Graphen der drei Funktionen können durch Setzen der Häkchen sichtbar (bzw. unsichtbar) gemacht werden.
Aufgabe:
Untersuche die Funktionen im Applet und begründe anschließend die Existenz der Summenregel in mathematischer Fachsprache (verwende Begriffe wie z.B. Tangentensteigung, Steigungsdreieck, ...).
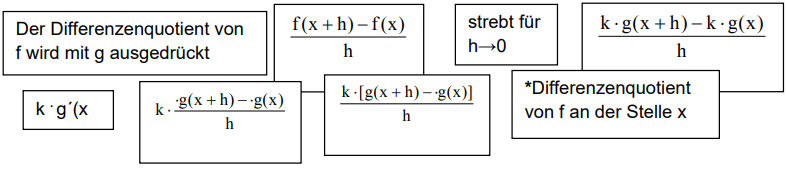
Zusatz: rechnerischer Beweis der Faktorregel

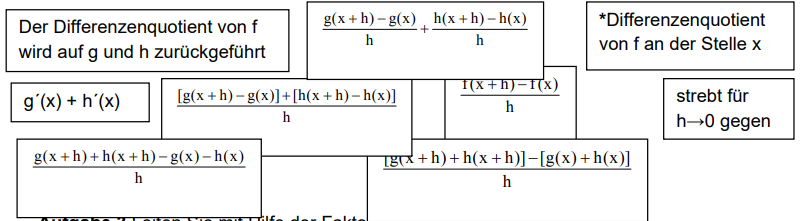
Beweise die Faktorregel mithilfe des Differenzenquotienten. Ordne dazu die Kärtchen. (Tipp: 1. Kärtchen ist mit * markiert.)
Zusatz: rechnerischer Beweis der Summenregel