-
Principios de Modelación Matemática Mónica Garza
-
1. Functions
- RELATIONS AND FUNCTIONS
- Solving Linear Equations
- Linear Equation Generator
-
2. Linear Functions
- Actividad 1: Página Geogebra Mónica Garza
- Graph the Line
-
3. Quadratic Functions
- drawing quadratic equations
-
4. Polynomial Functions
- Graphs of polynomials
This activity is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original activity or create your own copy for this Book instead?
This activity was created by '{$1}'. Do you want to modify the original activity or create your own copy instead?
This activity was created by '{$1}' and you lack the permission to edit it. Do you want to create your own copy instead and add it to the book?
Principios de Modelación Matemática Mónica Garza
mogarzamx, Jan 21, 2023
Main topics Principles of Mathematical Modelling
Table of Contents
- Functions
- RELATIONS AND FUNCTIONS
- Solving Linear Equations
- Linear Equation Generator
- Linear Functions
- Actividad 1: Página Geogebra Mónica Garza
- Graph the Line
- Quadratic Functions
- drawing quadratic equations
- Polynomial Functions
- Graphs of polynomials
RELATIONS AND FUNCTIONS
RELATIONS AND FUNCTIONS
Actividad 1: Página Geogebra Mónica Garza
Linear Functions
Identify the slope, and build the equation of the line in slope intercept form.
Equation of the line Fuente: https://youtu.be/BtcKotD6Ni8
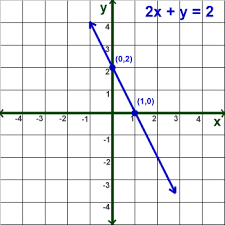
Rewrite equation in slope intercept form
Homework: Match the graph with the equations Fuente: https://cdn.kutasoftware.com/Worksheets/Alg1/Graphing%20Lines%20SI.pdf
Extra practice and examples:
In the given equation , the value of 5 is:
Determine the equation that represents the following linear function (in slope intercept form)
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
drawing quadratic equations
Exploring quadratic graphs
Graphing quadratic equations
Graphs of polynomials
THIRD-DEGREE POLYNOMIALS
The graph shows the polynomial . Investigate how the coefficients affect the shape of the graph.
TIP: How to effectively work with sliders.
Start by moving only the slider and observe how the graph changes. Then return its value back to 1.
Move the slider . What happens with the graph? When finished, set it back to 0.
Change the value of . Observe. Return to 0.
Move the slider .
Once you tried sliders individually, you can investigate what happens when you change more coefficients at the same time.
Leading coefficient
Describe how the value of affects the graph of a third-degree polynomial.
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
Constant coefficient
What point does the coefficient represent on the graph?
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
y-intercept
As you are changing the coefficients, the graph of a third-degree polynomial is also changing.
However, there are certain patterns that can be generalized for all third degree polynomials.
Use the applet to describe possible cases of graphs and answer the following questions.
Zeros (x-intercepts)
How many zeros can a third-degree polynomial have? Consider all possible cases.
Turning points and terrace points
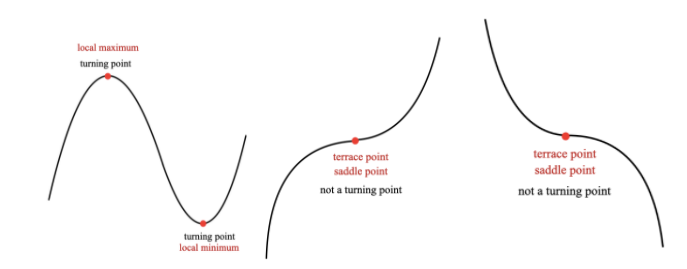
Turning points
What is the MAXIMUM NUMBER of turning points that a third-degree polynomial can have?
(Turning point: local minimum or local maximum)
Terrace points
What is the MAXIMUM number of TERRACE POINTS that a third-degree polynomial can have?
FOURTH-DEGREE POLYNOMIALS
You will now be investigating graphs of fourth-degree polynomials.
Read the tip about working with the sliders.
Zeros
How many zeros can a fourth-degree polynomial have?
Turning points
What is the MAXIMUM NUMBER of turning points that a fourth-degree polynomial can have?
(Turning point: local minimum or local maximum)
Terrace points
What is the MAXIMUM number of terrace points that a fourth-degree polynomial can have?
Higher-degree polynomials
The following applet allows you to analyze also some higher degree polynomials.
Your goal is to derive a general rule about the number of zeros and turning points of an n-th degree polynomial - see statements below.
GENERAL RULE about the number of ZEROS of a polynomial of n-th degree.
Complete the statement:
Polynomials of degree have at most ......... real zeros.
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
n
GENERAL RULE about the number of TURNING POINTS of a polynomial of n-th degree.
Complete the statement.
Polynomials of degree have at most ....... turning points.
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
n-1
Saving…
All changes saved
Error
A timeout occurred. Trying to re-save …
Sorry, but the server is not responding. Please wait a few minutes and then try to save again.