Analytische Geometrie, Q2
Q2, Heseen
Table of Contents
- Lineare Gleichungssysteme
- Lösungen von LGS
- LGS geometrisch interpretieren
- LGS geometrisch interpretieren II
- Orientieren im Raum
- Punkte im Raum
- Vektoren im Raum - Einstieg
- Geraden
- Geradenscharen: Würfel
- Abstandsberechnungen
- Abstand Punkt Gerade
- Über den Wolken
- Ebenen
- Kreuzprodukt
- Vektorprodukt-Trainer
- OHIMI Aufgaben
- Symmetrie Nachweisen, LGS interpretieren
Lösungen von LGS
Formen Sie das Lineare Gleichungssystem mithilfe des Applets um und bringen Sie es in die "Dreiecksform"[br][math]x-y-z=-1[/math][br][math]2x+2y-10z=2[/math][br][math]x+3y-9z=3[/math][br][br][b]Hinweise:[/b][br][list][*]Klicken Sie in die weißen Felder und tragen Sie die Koeffizienten des LGS oben ein.[/*][*]Durch Klick in die blauen Felder und Verwendung des Schiebereglers können Sie die Rechenoperationen einstellen, die zur Anwendung des Gauß-Verfahrens angewendet werden sollen.[/*][/list]
Ihre Umformungen waren korrekt, wenn Sie in der letzten Zeile [br][math]0x+0y+0z=0[/math][br]erhalten.[br][list][*]Erklären Sie die Bedeutung dieses Ausdruckes.[/*][*]Hat das Gleichungssystem dennoch eine Lösungsmenge?[br]Wenn ja: Berechnen Sie diese und kreuzen Sie Ihre Vermutung an (zwei Antworten sind korrekt).[/*][/list]
Lineare Gleichungssysteme im Sachzusammenhang Aufgabe "Versandhandel"
Verwenden Sie das Rechenschema zur Bestimmung der Lösung für die Aufgabe "Versandhandel"
Lösung zur Aufgabe Versandhandel
x=330, y=250, c=120.[br]Das Lager kann also geräumt werden mit 330-mal Sortiment 1, 250-mal Sortiment 2 und 120-mal Sortiment 3.
Punkte im Raum
Lage von Punkten im Raum beschreiben
[b]Information:[/b][br]Mit diesem dynamischen Arbeitsblatt können Sie lernen, sich im dreidimensionalen Raum zu orientieren.[br][br][b]Und los geht's:[/b][br]Im Applet unten sehen Sie ein dreidimensionales Koordinatensystem und insgesamt sechs Schieberegler, mit denen verschiedene Einstellungen vorgenommen werden können.[br][br]Untersuchen Sie den Einfluss der Schieberegler, indem Sie diese durch Klicken und Ziehen verändern. Beantworten Sie die anschließenden Fragen.[br]
Bedeutung der Schieberegler
Erklären Sie in Stichworten, welche Einstellungen Sie mit den Schiebereglern vornehmen können.[br]Beschreiben Sie genau, wie sich die Lage des blauen Punktes im Koordinatensystem ändert, wenn die Schieberegler px, py, pz bewegt werden.
Unterschied Punkt/ Ortsvektor
Im Applet oben können Sie einen blauen Punkt sehen. Die Auswirkung der entsprechenden Schieberegler haben Sie bereits erkundet.[br]Oben wird der Begriff "Ortsvektor" verwendet. Versuchen Sie den Unterschied zwischen den Begriffen "Punkt" und "Ortsvektor" zu beschreiben.
Bedeutung der Koordinatenebenen
Im Applet weiter oben sind drei Ebenen zu sehen.[br]Es sind diese die [br]x-y-Ebene[br]x-z-Ebene[br]y-z-Ebene.[br]Geben Sie die Farbe der jeweiligen Koordinatenebene an.[br]Sollten Sie mit dem Begriff "Koordinateneben" nichts anfangen können, informieren Sie sich im Fachbuch darüber.
Punktkoordinaten
Geben Sie die Koordinaten eines Punktes P an, der die folgenden Eigenschaften besitzt (Sie können immer noch das Applet ganz oben nutzen):[br]1.) Der Punkt P liegt in der x-y-Ebene[br]2.) Der Punkt P hat eine Höhe von 4 Längeneinheiten (LE)[br]3.) Der Punkt P ergibt sich durch eine Spiegelung des Punktes Q(1 | -2 | -3) an der y-z-Ebene
Sie dürfen als Baumeister für den ehrwürdigen Pharao TutMathMatik einspringen.
[b]BAUAUFTRAG:[/b] [br]Bauen Sie dem Pharao eine Pyramide mit quadratischer Grundfläche, wobei die Seiten jeweils 5 LE lang sein sollen. Die Spitze soll in der Mitte über der Grundfläche ebenfalls 5 LE hoch sein.[br][br][b]Hinweise zur Arbeit mit dem Applet:[/b][br][list][*]Die Punkte werden in Klammern in der Eingabezeile eingegeben: Z.B. (-1,3,6).[/*][*]"Komma-Werte" werden mit einem . eingegeben: z.B. 4,5 ==> 4.5[/*][*]Klicken Sie auf den zweiten Button von Links und dann auf die entsprechenden Punkte, um zwei Punkte mit einer Linie zu verbinden.[/*][*]Klicken Sie auf den dritten Button von links und dann auf die Eckpunkte einer Fläche, um z.B. 3 Punkte zu einer Fläche zu verbinden.[/*][*]Klicken Sie auf den Button mit dem Pfeil. Wenn Sie dann im Applet die linke Maustaste gedrückt halten und die Maus bewegen, bewegt sich das Koordinatensystem. So können Sie Ihr Ergebnis von allen Seiten aus betrachten.[/*][/list][br][b]TIPP:[/b] [br]Wenn Sie überlegen, an welcher Stelle über der Bodenfläche die Spitze liegen muss, kann auch der richtige Punkt leicht gefunden werden. Eventuell hilft eine Skizze von Hand mit den Seitenlängen. Sie können die Lage des Mittelpunktes auch mit Hilfe der Linien ausprobieren.
Geradenscharen: Würfel
Gegeben ist ein Würfel mit der Kantenlänge 4.[br]Die Gerade g verbindet die Seitenmitte M[sub]1[/sub] und M[sub]2[/sub] der Kanten EH und BF (siehe dynamische Abbildung).[br]Eine Schar h[sub]t[/sub] von Geraden verläuft durch den Punkt E und einen Punkt P[sub]t[/sub] auf der Kante CG.[br]Untersuchen Sie, ob eine Gerade dieser Schar die Gerade g schneidet.[br][br]Die Ergebnisse erhalten Sie durch Klick auf "Antworten überprüfen"[br][br][b]Hinweis:[/b][br]Verwenden Sie als Parameter für die Gerade g den Buchstaben k.[br]Verwendet Sie als Parameter für die Gerade h[sub]t[/sub] die Buchstaben r und t.[br][br]Quelle: EdM, Q2, Seite 67, Nr. 24, Westermann Verlag.
Lösungshinweise erhalten Sie durch Klick auf "Antworten überprüfen"
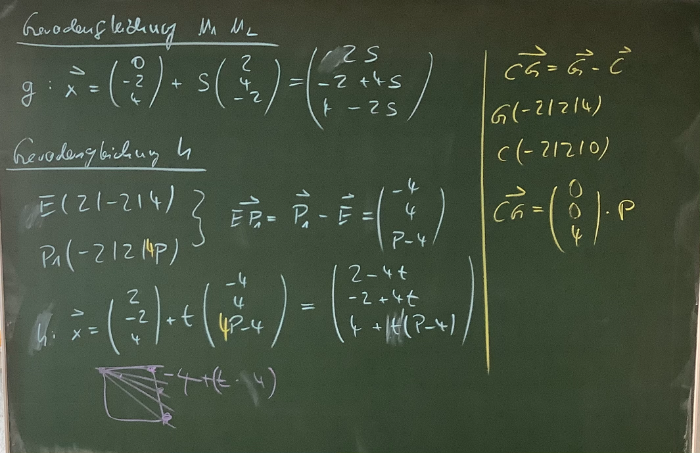
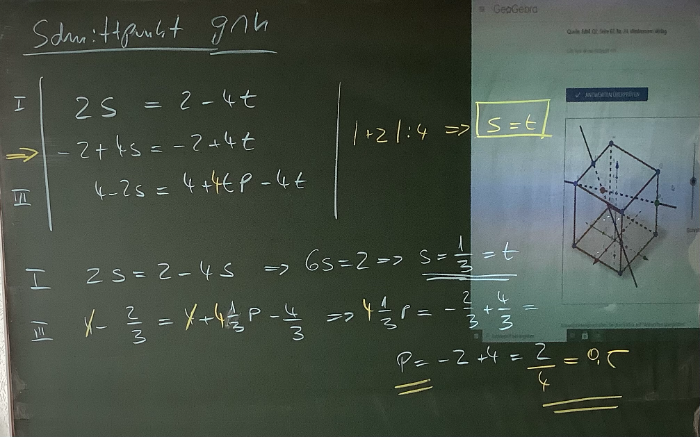
Abstand Punkt Gerade
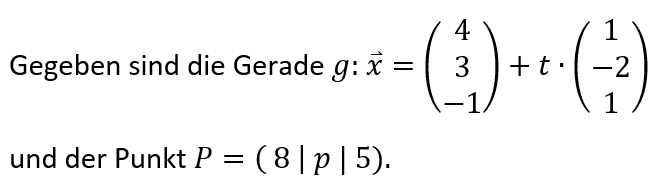
Teilaufgabe 1:
Begründen Sie rechnerisch unter Kommentierung Ihrer Rechenschritte, das der Punkt P für keinen Wert p auf der Geraden g liegt.
Teilaufgabe 2
Bestimmen Sie die fehlende Koordinate p des Punktes P so, dass der Abstand von P zu g 5 LE beträgt.[br][br][b]Hinweise zur Vorgehensweise:[/b][br]Machen Sie sich zunächst die Situation mithilfe der Abbildung 1 klar. Experimentieren Sie damit.[br]Versuchen Sie die möglichen Ergebnisse zu ermitteln.[br]Überlegen Sie sich eine Rechenstrategie, wie Sie die fehlende Koordinate rechnerisch bestimmen können.[br][br][b]Vielleicht können Ihnen auch die nachfolgenden Hinweise bei der Lösung der Aufgabe helfen (klicken Sie auf ANTWORTEN ÜBERPRÜFEN).[/b]
Vektorprodukt-Trainer
Kurze Wiederholung: Kreuzen Sie die Aussagen an, die für das Vektorprodukt zutreffen.
[b]Hinweise:[/b][br][list][*]Durch Klicken auf die Schaltfläche links oben im Applet wird eine neue Aufgaben erzeugt.[/*][*]Klicken Sie in das obere Feld der Lösung und geben Sie die von Ihnen berechneten Koordinaten ein. Mit der TAB Taste springen Sie zum nächsten Feld.[/*][*]Durch Klick auf die Taste Prüfen .... selbsterklärend.[/*][*]Im Anschluss an den Rechner finden Sie ein Infoblatt zum Vektorprodukt und darunter weitere Verzweigungen zu Themen der Oberstufe[/*][/list][br][b]Möglichkeiten zum Selbststudium:[/b][br][list][*]Berechnen Sie das Vektorprodukt händisch und mit dem TR[/*][*]Klicken Sie auf den Link "Mathematik Oberstufe" und schauen Sie sich die Präsentation mit den Verweisen zu den unterschiedlichen Themenbereichen an.[/*][/list]
Vektorprodukt
siehe auch:
[url=https://www.geogebra.org/m/fmgpeeam][size=150][color=#0000ff]Mathematik der Oberstufe[/color][/size][br][/url]
Symmetrie Nachweisen, LGS interpretieren
[b]Hinweise:[/b][br][list][*]Die Aufgaben sind ohne Hilfsmittel zu bearbeiten.[/*][*]Für die Bearbeitung beider Aufgaben stehen Ihnen 20 Minuten zur Verfügung.[br][br][/*][/list][b]Mögliche Zeiteinteilung:[/b][br][list][*]5 Minuten: beide Aufgaben durchlesen, Lösungsstrategien überlegen, im Text der Aufgabe vorhandene Informationen sinnvoll nutzen, kleine Notizen oder Skizzen machen, Nachdenken, Wissen aktivieren, [/*][*]15 Minuten: Aufgaben bearbeiten.[/*][/list][br][b]Lösung:[/b][br]Die Applets am Ende der Seite können zur Überprüfung der Lösung eingesetzt werden.
Aufgabe 3: LGS geometrisch interpretieren
Aufgabe 4: Symmetrie einer geometrischen Form nachweisen
