van functie naar spinnenwebmodel
Wat is een spinnenwebmodel? In dit boek volg je de opbouw vanuit functies over iteraties. Verken hoe vraag- en aanbod elkaar kunnen beïnvloeden en in een iteratief proces kunnen convergeren of divergeren. In een laatste bestand kan je de opbouw van een iteratie zowel volgen met een schuifknop in het tekenvenster als kolom na kolom in het rekenblad.
Table of Contents
- webgrafieken
- van functie naar iteratie
- iteratie voorgesteld in een webgrafiek
- afgeremde groei
- spinnenwebmodel
- convergentie en divergentie
- onderzoek convergentie
- voorbeeld
- van startprijs naar evenwichtsprijs
- spinwebmodel en iteratie via het rekenblad
van functie naar iteratie
functie
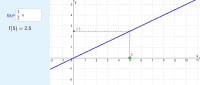
Bij een functie geeft een functievoorschrift het verband weer tussen een onafhankelijke veranderlijke en een afhankelijke veranderlijke. [br]Hierbij hoort bij elke invoerwaarde hoogstens één uitvoerwaarde.[br]In een functiewaardentabel kan je een overzicht geven van invoerwaarden en bijhorende uitvoerwaarden.[br]Neem bijvoorbeeld de functie [math]f\left(x\right)=\frac{1}{2}x[/math] [br][list][*]Bij de invoerwaarde 5 vind je 2.5 als beeld.[/*][*]Het punt [math]\left(5,2.5\right)[/math] ligt op de grafiek van f.[/*][/list]
iteratie
Bij een iteratie bereken je geen lijst van functiewaarden bij gegeven invoerwaarden, maar vormt de beeldwaarde van een gegeven vertrekwaarde de invoerwaarde van de volgende stap. Zo vorm je een rij van waarden die telkens de beeldwaarde zijn van de vorige waarde.[br][list][*]Vertrek je van dezelfde functie [math]f\left(x\right)=\frac{1}{2}x[/math] en een startwaarde 20[br]dan bekom je volgende rij: 20, 10, 5, 2.5, 1.25, ...[/*][*]Zet je deze waarden uit in een tijd-waarden grafiek dan merk je dat ze onbegrensd kleiner worden.[br]Je zegt dat de rij convergeert naar 0.[/*][/list]
Hoe doe je het zelf in GeoGebra
[b]N = Rij(Iteratie(f, x[sub]0[/sub], n), n, 0 stappen)[/b] creëert een rij met iteratiewaarden. Hierin is[br][list][*]f de functie die telkens wordt toegepast[/*][*]x[sub]0[/sub] de startwaarde[/*][*]n het aantal iteratiestappen van 0 tot de waarde 'stappen', bepaald in een invulvak.[/*][/list][b]Eerste(Rij((nn - 1, N(nn)), nn, 1, stappen + 1), n + 1)[/b] creëert een rij punten in het tekenvenster, waarbij een schuifknop n het aantal iteraties bepaalt.[br]Opmerking: Als teller voor het aantal punten kies je [i]n + 1[/i], omdat je zowel de beginwaarde als de n iteraties wil tonen.
convergentie en divergentie
spinnenwebmodel
In onderstaande applet zie je een [color=#0000ff]aanbodfunctie a[/color] en een [color=#ff0000]vraagfunctie [/color]v.[br][list][*]Voor een gegeven hoeveelheid [b]h[sub]1[/sub][/b] op de horizontale as kan je op de [color=#ff0000]vraagfunctie [/color]de overeenkomstige prijs [b]p[sub]1[/sub][/b] aflezen. Deze prijs zal op zijn beurt weer het aanbod bepalen.[/*][*]Trek vanaf (0, p[sub]1[/sub]) een horizontale lijn en bepaal het snijpunt met de aanbodfunctie.[br]De x-coördinaat van dit snijpunt is een nieuwe hoeveelheid [b]h[sub]2[/sub][/b].[/*][*]Met deze hoeveelheid [b]h[sub]2[/sub][/b] komt weer een nieuwe prijs [b]p[sub]2[/sub][/b] overeen enz.[/*][/list]Volg je de iteratie dan zullen aanbod en prijs naar een evenwichtssituatie evolueren.
convergentie en divergentie
In het applet kan je twee dingen wijzigen: de beginhoeveelheid en de grafiek van de vraagfunctie.[br][br]Wijzig de grafiek van de [color=#ff0000]vraagfunctie [/color]door het rode punt te verslepen. [br][list][*]Blijft het model altijd convergeren?[br][/*][*]Hoe kan je zelfs aan de eerste iteraties zien of een model convergeert?[/*][/list]