Parallel Lines and Transversals
Foundations course G.CO8-9
Table of Contents
- Parallel Lines
- Parallel Lines
- Reading and Writing Parallel Line Math Language
- Transversals
- Copy of Transversal Intersects Parallel Lines
- Supplementary Angles
- Supplementary Angles
Parallel Lines
[size=150][b][color=#351c75]Parallel lines are lines that are on the same plane (surface) that are equal distance from one another and therefore, never [url=https://www.mathopenref.com/intersection.html]intersect.[/url] [/color][/b][/size]
Explicit Instruction: Parallel Lines
[b][color=#9900ff][size=150]We often think of train tracks when we try to make a picture in our minds of what parallel lines look like. We know the rails on which the wheels of the train run on, have to be equal distance or the train would fall off the track. We know they do not ever meet as well. [/size][/color][/b]
[b][color=#ff0000][size=150]Parallel lines can help us to measure angles so we do not have to use a protractor. This week we will learn how parallel lines can help us to measure angles. [/size][/color][/b]
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
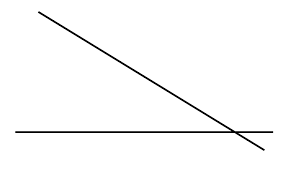
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
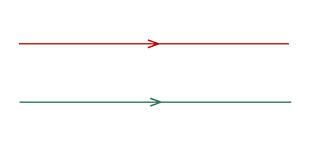
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
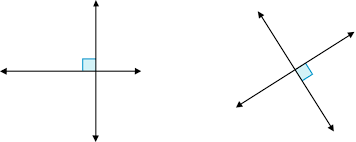
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
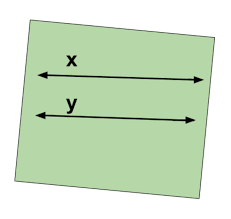
[b][color=#1c4587][size=150]In the image above, are the lines parallel or not parallel?[/size][/color][/b]
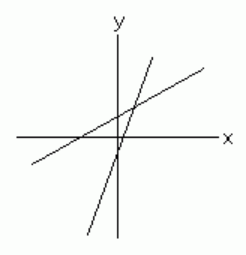
[size=150][b][color=#ff0000]In the image above, can you find a pair of parallel lines? [/color][/b][/size]
Copy of Transversal Intersects Parallel Lines
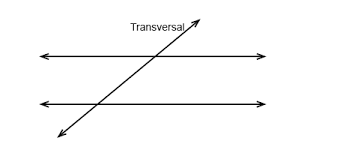
[size=200][b][color=#ff0000]A line that crosses two lines is called a TRANSVERSAL. [/color][/b][/size]
[size=150][b][color=#0000ff]If we draw two parallel lines and then draw a line transversal through them, we will get eight different angles. [/color][/b][/size]
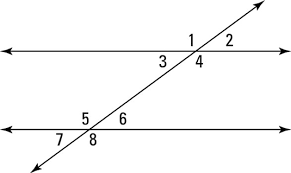
[size=200][b][color=#ff0000]Interior/Exterior Angles in a Transversal. [/color][/b][/size]
[size=150][b][color=#1155cc]The angles [i]between [/i]the parallel lines are called the interior angles. [/color][/b][/size]
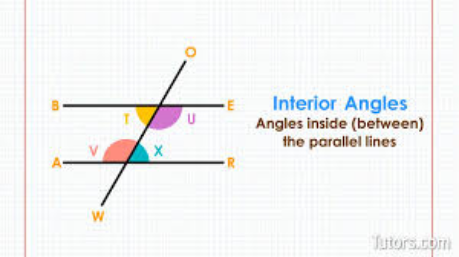
[b][color=#1155cc][size=150]The angles that are on the outside of the parallel lines are called exterior angles. [/size][/color][/b]
Exterior Angles
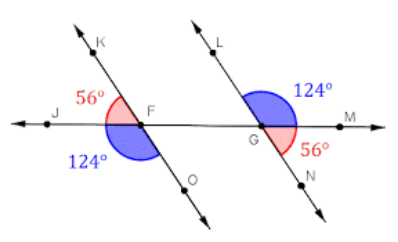
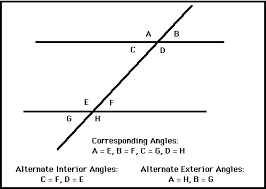
[size=200][b][color=#ff0000]Alternate/Corresponding Angles in a Transversal[/color][/b][/size]
Example of a corresponding angle
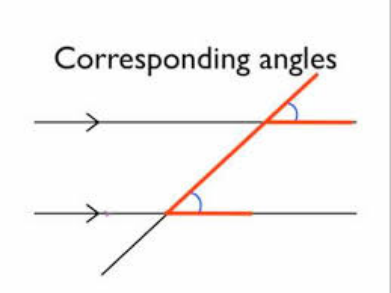
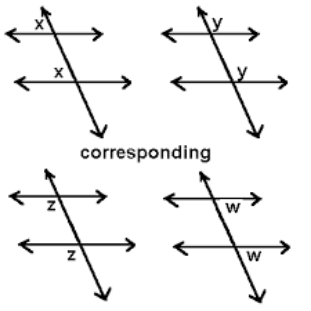
[b][color=#85200c][size=150]Corresponding angles are matching angles on the same side of the transversal. Study the image below to see all corresponding angles in a transversal. [/size][/color][/b]
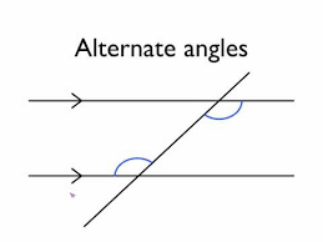
[size=150][b][color=#0000ff]Alternate angles are matching angles that are across from each other on the transversal. [/color][/b][/size]
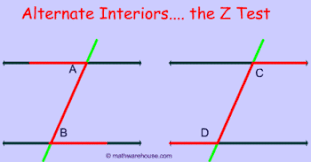
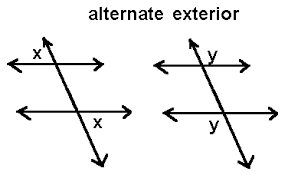
[b][color=#a61c00][size=150]Use the Interactive and the chart below to learn the locations of interior, exterior, corresponding and alternate angles in a transversal. [/size][/color][/b]
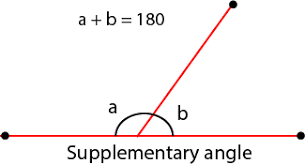
Supplementary Angles
[size=150][b][color=#ff0000]Supplementary Angles are any pair of angles whose sum (adding) is equal to 180 degrees ([url=https://www.mathopenref.com/anglestraight.html]straight angle[/url]). [/color][/b][/size]
Explicit Instruction: Supplementary Angles
[size=150][b][color=#351c75]Remember that pairs are things that come in twos. For example, the pair of dice above is called a pair because there are two of them. Can you think of any other types of pairs? [/color][/b][/size]
Supplemental Angles
[size=200][b][color=#ff0000]So, any PAIR of angles that have a [url=https://www.mathsisfun.com/definitions/sum.html]sum[/url] of 180 degrees are supplementary angles. [/color][/b][/size]
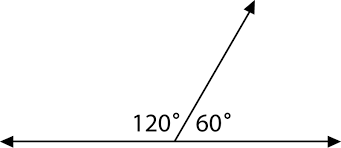
[size=150][b][color=#0000ff]We can use that truth to solve problems in Geometry![/color][/b][/size]
Supplemental Angle Problem
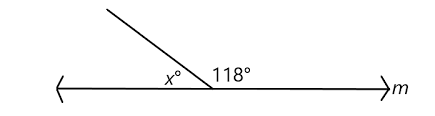
[b][color=#ff0000]We know that line m is a straight line. [br][/color][/b][b][color=#ff0000]If line m is a straight line, then we know its measure is 180 degrees[br]We know that the larger angle has a measure of 118 degrees, but we don't know what the measure of its supplemental angle is (x[math]^\circ[/math][/color][/b][size=150][b][color=#ff0000]).[/color][/b][/size]
[size=150][b][color=#0000ff]I set up an equation based on the postulate: [/color][/b][/size] [size=150][b][color=#b45f06]x + 118 = 180[/color][/b][/size][br][b][size=150][color=#0000ff][br]I subtract 118 from both sides of the equal sign [/color][color=#b45f06]x = 62[/color][/size][/b]