置換のあみだくじ化
あみだくじはどんな置換も作れるか?
[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/b][br][br]3本線のあみだは3つの番号{1,2,3}の順列、置換と同じであることはわかった。[br][br]たて線が4本以上のn本のときのn本あみだは,n番号の置換になることは予想できる。[br]しかし、実際に任意のn!もある置換のすべてをあみだくじで表現できるのだろうか?[br][br]この問は、「あみだは置換」か?[br]ではなく、「置換はあみだ」か?[br][br]と言い換えることもできるね。
0.そもそも置換ってなんだっけ?
[b]<写像と演算>[br][size=150](写像)[/size][br][/b]要素、たとえば、番号の集めた集合を考えてみよう。[br]整数0からn-1まで集めた集合をZnと呼ぼう。[br]たとえば、Z5={0,1,2,3,4}だ。[br]X=Z5, Y=Z30とするとき、[br]Xの要素xを2乗したものをYの要素yに対応させる関数fを考えよう。[br]関数fは(x,y)のペアで表すことができるね。[br](0,0),(1,1),(2,4),(3,9),(4,16}[br]数と数の対応を関数というけど、[br]数にかぎらず広げたものが写像です。[br]写像f:X→Y[br]と対応する集合でかいたり、[br]写像f:x→x[sup]2[/sup][br]と対応する要素の記号を数式でかいたりする。[br]Xを始域、定義域、Yを終域と呼ぶこともあるね。[br]写像はふつう、始域と終域がちがっていてもよい。[br][br][b][size=150](全射と単射と全単射)[br][/size][/b]Yの中でXがfで写った先、[b]f(X)[/b]={y| x∈X, y=f(x)}= {0,1,4,9,16}を[b]像image、値域[/b]といい、[br][b]imf[/b]とかいたりする。[br]ここで大切なことの1つめは、Xの要素が変わると、Yも変わることだ。[br]Xのお相手は別々であり、Xのお相手がYの中でかぶる、モテモテのYはない。[br]これを[b]単射[/b]という。[br][br]さらに大切なのは、f(X)がYと一致するとはかぎらないということだ。[br]f(X)はYの中ではスカスカになっていて隙間がある。f(X)に関係ないYの要素がある。[br]それに対してちがう状況を作ってみよう。[br]X=Z5, Y=Z5として[br][b]id [/b]: x→xという何もしない写像、[b]恒等写像[/b]を考えよう。[br]すると、f(X)=Yとなり、f(X)はYの全部に入っているから、[br]Yはぜんぶf(X)で写ってきているので[b]全射[/b]という。[br][br][b][size=150](逆写像)[/size][/b][br]写像f:X→Yと写像g:Y→Zを続けて行うと、[br]x→f(x)→g(f(x))となる。この操作をまとめて、[br]x→g*f(x)とかくことにすると、[br]g*f:X→Z[br]g*f:x→g(f(x))[br]のように、写像が合成できる。[br][br]写像f:X→Yと写像g:Y→Xについて、[br]その合成が恒等写像になるとき、つまり、f*g=id で g*f=id[br]gはfの逆写像(inverse)といい、f[sup]-1[/sup]とかくことがある。[br]fが全単射(全射で単射)であることと、fに逆写像があることは同値ですね。[br][br][b][size=150](演算で閉じている)[/size][/b][br]集合Xの要素x,yから2つを選び、その演算*の結果の要素zを求めることは[br]要素かくと、x*y=zになるね。[br]これを要素の写像でかくと、[br]*: (x, y) →z[br]とかけるね。[br]これを集合でかくと、同じ集合Xから任意の2要素を選ぶことは積の法則からn(X)[sup]2[/sup]通りあるね。[br]要素の組自体をX×XとかX[sup]2[/sup]とかき直積と呼ぶ。積集合は集合の重なりの意味で使うため。[br]*:X[sup]2[/sup]→Z[br]演算結果がXに属するときは、演算で閉じているという。集合でもわかるようにかこう。[br]*:X[sup]2[/sup]→X[br][color=#0000ff](例)[/color][br]たとえば、2項演算×、+は整数Zでは閉じているので次のようにかけるね。[br]+:Z[sup]2[/sup]→Z[br]×:Z[sup]2[/sup]→Z[br][color=#0000ff](例)[/color][br]たとえば、G={100,2000}, R={0.03, 0.05, 0.08, 0.1} Gが税抜き価格、Rが歴代の消費税率[br]それぞれの税額Yを計算すると、[br]×:G×R→Y[br]G×R={(100, 0.03),(100,0.05),(100,0.08),(100,0.1), (2000,0.03), (2000,0.05), (2000, 0.08),(2000,0.1)}[br]Y={3, 5, 8, 10, 60, 100, 160, 200}[br][br][b][size=150](置換はどんな写像か?)[br][/size][/b]置換は、番号の集合から番号の集合への写像だ。[br]とくに、決まった数式で移しているわけでなくてもよいので、関数である必要はない。[br]ただ、始域の番号が、終域に移ればよいわけだ。[br]たとえば、巡回群(1 2 3)は[br]1→2, 2→3,3→1という動きをしているので、[br]写像としてとらえるとX={1,2,3}[br]f:X→X[br]f(1)=2, f(2)=3,f(3)=1[br]のように対応をはっきりとかくことができる。[br]だから、写像だ。[br]しかも、別ものが集中するようなf(1)=f(2)のようなこともないので単射だ。[br]そして、写ったあとのどの番号を逆にたどることもできるので全射だ。[br]全単射の写像だと言える。[br]ただし、恒等写像とは限らず、番号の置き換え、置換をさまざま表現できる写像だね。[br]だから、通常の番号や数の変換とちがって、[br]番号は順序や大きさを表すものというよりも、ただ、区別のための名前というイメージを[br]取り組もう。[br]関数のような簡単な数式をすぐに求めるのではなく、要素の関係性、集合の関係性を[br][br]ていねいに追いかけるという姿勢が必要でしょう。
1.置換を互換の積にする
[b][size=150]<置換→巡回置換の積→1要素共有互換の積>[/size][br](置換は巡回置換の積に直せる)[/b][br]どんな置換にも、1→a, a→b, b→.....→1のようなループサイクルがあるね。[br]X={1,2,3,....., n}[br]置換f:X→X[br]とすると、n個の要素の一部分m個でループができる。つまり、m個の巡回置換ができる。[br]こんどは、残ったn-m個の要素で同じようなループを探すことができる。[br]だから、これを繰り返すことで、[br][color=#0000ff][size=150][b]置換は互いにかぶらない巡回置換の積に直せる。・・・・★[br][/b][/size][/color][br][b](巡回置換は1要素共有の互換の積に直せる)[/b][br]たとえば、[br](実験)[br]巡回置換(2 4 6 8)を先頭が必ず含まれる互換(2 4),(2 6),(2 8)の積で表そう。[br]巡回置換は2→4, 4→6, 6→8,8→2の番号の入れ替えをサイクリックに行っている。[br]一方の互換は(2 a)は2→aとa→2の交換を同時におこなう。[br]巡回置換で終点か始点に2があるのは、2→4と8→2だ。[br]一方で、終点にも始点にも2がないのは、間に2をはさむと実現できる。[br]4→6は 4→2→6 [br]6→8は、 6→2→8。[br][br]だからこの4つの巡回を実現するための互換の順番は(2 4),( 2 6), (2 8)の順に実行する。[br]2→4は 2→4[br]8→2は 8→2[br]4→6は 4→2→6 [br]6→8は 6→2→8[br]つまり、(2 4 6 8)=( 2 8)(2 6)(2 4) と互換を実行する順に右から並べる。[br][br][size=150][b](一般化)[br]巡回置換(x a b c d e f )を1要素共有互換(x a),(x b),(x c)[size=150],(x d)[/size][/b][b][size=150],(x e)[/size][/b][b][size=150],(x f)[/size][/b][b]の積で表そう。[br][/b][size=100]x→aは x→a[br]a→bは a→x→b [br][size=150]b→cは b→x→c [br][/size][size=150]c→dは c→x→d [br][/size][size=150]d→eは d→x→e [br][/size][size=150]e→fは e→x→f [br][/size][size=150]f→xは f→x [br][/size][/size][b]つまり、[br][color=#0000ff]巡回置換は1要素共有互換の積で実現できる[br][/color][size=150][color=#0000ff](x a b c d e f )=(x f)(x e)(x d)[b][size=150](x c)[/size][/b][b][size=150](x b)[/size][/b][b][size=150](x a)[b]・・・・★0[br][/b][/size][/b][/color][/size][/b][/size][color=#9900ff][b][size=150][u]質問:巡回置換は1要素共有互換の積をコードで確かめるにはどうしましょう。[br][/u][/size][/b][/color][br]基本となる巡回置換(リスト形式)を辞書に変えるami2dic関数、[br]置換aによるkの行先を返すami_go関数は前回と同じ。[br]リスト形式の互換、置換の辞書のリスト(のリスト)から互換・置換の積を辞書で返す[br][b]polymulti(gokan_Lst)、polymultiR([b]gokan_Lst[/b])[/b]を新しく作ろう。[br]そして、たとえば、gokans=[[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]をamis2dicsで辞書リストにしてから、[br]polymultiRに入れる。[br]名前で比較するため、Nlist=rotdic(S,SN) をしておく。[br]g=[1,7,6,5,4,3,2]をami2dicに入れた結果の辞書が同じになることを確認してみよう。[br][color=#0000ff][IN]Python================================================[br][/color]def polymulti(gokan_Lst):[br] listsize=len(gokan_Lst)[br] a = gokan_Lst[0][br] for num in range(1,listsize):[br] b = gokan_Lst[num][br] a = [b]conL(a,b)[/b][br] dic = a[br] #空の辞書は形式的に単位元とする。[br] if len(dic)==0:[br] dic[1]=1[br] return dic[br]#互換の連続(互換辞書のリストgokan_lstをとり左から連続的に演算して名前を返す)[br]def polymultiR(gokan_Lst):[br] listsize=len(gokan_Lst)[br] a = gokan_Lst[0][br] for num in range(1,listsize):[br] b = gokan_Lst[num][br] a = [b]conR(a,b)[/b][br] dic = a[br] #空の辞書は形式的に単位元とする。[br] if len(dic)==0:[br] dic[1]=1[br] return dic[br] [br]a=[1,2][br]b=[1,3][br]c=[1,4][br]d=[1,5][br]e=[1,6][br]f=[1,7][br]g=[1,7,6,5,4,3,2][br]gokans =[a,b,c,d,e,f][br]S=[a,b,c,d,e,f,g][br]SN=["a","b","c","d","e","f","g"][br]Nlist=rotdic(S,SN) # 名前表示のため[br][br]gokansdics=amis2dics(gokans)[br]print(name(polymultiR(gokansdics)))[br]print(name(ami2dic(g)))[br]#=============================================[br][OUT][br]g[br]g
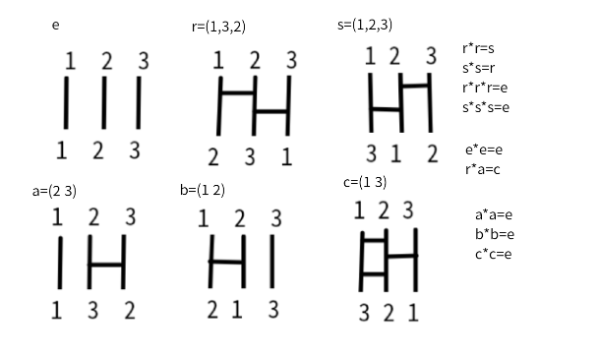
3本だけのあみだくじを使って、置換と互換の法則を確認しよう。

2.どんな互換もあみだくじに直せるか
[b]<(1n)互換を隣接互換(ヨコ線)の積で表す。>[br](実験)[/b][br]あみだくじのヨコ線は隣接互換でした。[br]3本あみだくじの(12)(23)(12)が互換(13)になることも知りました。[br]そのときのかぎは、最初と最後が同じ隣接互換(12)だったことです。[br]だから、最初のヨコ線2→1のあと、最後に1→2があるから、1をつなぐと2→2になったのでした。[br]それに対して1回だけヨコ線ある3は真ん中で3→2となり最後に2→1となり、3→2→1です。[br]残りの1は次々の線を変えて1→2→3となります。結局(13)となるのでした。[br]4本あみだで同じような積を作ってみましょう。[br](12)(23)(34)(23)(12)はどうなるでしょう。[br]もちろん、2→1→2で2はもとに戻ります。[br]さらに、3→2→3で3ももとに戻ります。[br]4は4→3→2→1と1まで移動し、1は反対に1→2→3→4と4まで移動して終わります。[br]だから、(14)になります。[br][b](一般化)[/b][br]あみだくじでは上下対称続く、隣接互換の積の式が左右対称に続くとき、[br]1はnまで移動してから終わり、nは1まで移動して終わり、他はもとに戻るか動かない。[br]だから、[br][color=#0000ff][b](12)(23)(34).......(n-2 n-1)[u](n-1 n)[/u] (n-2 n-1).........(34)(23)(12)=(1 n) ・・・・★1[br][/b][/color][br][b][size=150]<( i j )互換を隣接互換の積で表す>[br][size=100](実験)[/size][br][/size][/b]たとえば、10本あみだくじであっても互換(6 10)は★1の考えで作れるはずだ。[br]12345は動かす必要がなく、6789 10の線だけ使う。[br]すると★1の1にあたるものを6の線にすればよいだろう。[br]10−6=4で、1+4=5だから、6の位置を1番と思って★1の式をかこう。[br](12)(23)(34)(45)(34)(23)(12)=(15)[br]6の位置を1番と思っている式だから、1が6になるように互換の番号を6-1=5増やそう。[br](67)(78)(89)(9 10)(89)(78)(67)=(6 10)[br]となる。[br][b][size=150][size=100](一般化)[br][/size][/size][/b](i j) 互換の作成は(1 n) 互換の作成(★1)の移し替えでできる。[br][b](12)(23)(34).......(n-2 n-1)(n-1 n) (n-2 n-1).........(34)(23)(12)=(1 n)[/b][br]i-1=p とすると、n=j-pとなるから、互換の番号をpだけ増やせばよい。[br]すると、1は1+p=1+i-1=iになる。[br]ヨコ線は、i番からj番まで右下がりで連続して引き、j番からi番まで反転して左下がりに引けばよいね。[br][b][size=150][color=#0000ff](i i+1)(i+1 i+2).....(j-1 j) .....(i+1 i+2)(i i+1)= ( i j) [b]・・・・★2[/b][br][/color][/size][/b][br][color=#9900ff][u][b][size=150]質問:(12)(23)(34)(45)(34)(23)(12)=(15)、(67)(78)(89)(9 10)(89)(78)(67)=(6 10)をコードで確かめるにはどうしますか。[br][/size][/b][/u][/color][br][br][b][color=#0000ff]上で作ったpolymultiR関数に互換の辞書のリストを入れて、帰ってくる辞書を出力してみよう。[br][/color][/b]polymultiRにgokan=[[1,2],[2,3],[3,4],[4,5],[3,4],[2,3],[1,2]]を辞書に変換して入れて返ったものが[br][1,5]をami2dicに入れて返る辞書と同じかどうかを調べてみよう。[br]polymultiRにgokan=[[6,7],[7,8],[8,9],[9,10],[8,9],[7,8],[6,7]]を入れて返ったものが[br][6,10]をami2dicに入れて返る辞書と同じかどうかを調べてみよう。[br]互換どうしの比較は見た目でわかるので、名前づけしない。[br][color=#0000ff][IN]Python[br]#==============================================[br][/color][color=#0000ff]gokans=[[1,2],[2,3],[3,4],[4,5],[3,4],[2,3],[1,2]][br]goal=[1,5][br]print(polymultiR(amis2dics(gokans)))[br]print(ami2dic(goal))[br][br]gokans=[[6,7],[7,8],[8,9],[9,10],[8,9],[7,8],[6,7]][br]goal=[6,10][br]print(polymultiR(amis2dics(gokans)))[br]print(ami2dic(goal))[br]#================================================[br][/color][OUT][br]{1: 5, 5: 1}[br]{1: 5, 5: 1}[br]{10: 6, 6: 10}[br]{6: 10, 10: 6}[br]同じ辞書になるので、同じ置換だとわかるね。
3.まとめと演習
ここまでわかったことをまとめよう。[br][br]・前回は「あみだくじが置換群だ」とわかった。[br]あみだくじが番号の置換を表し、たてにつなぐことを演算とみなすと、[br]あみだくじどうしの2項演算は群であることがわかったね。[br][color=#0000ff]群は[b]閉じ[/b]ていて、[b]なにもしない要素[/b](単位元、零元)があり、[b]逆もどしの要素[/b](逆元)がある。[br]このようなつながりのある要素の集合が[b]群[/b]だった。[br][/color][br]・今回は「置換群はあみだくじにできる」とわかった。[br]どんな置換でも、つぎつぎと変換することで、最終的には隣接互換の積、つまり[br]あみだくじに直せることがわかったね。[br]具体的には、次のステップで置換をあみだくじに表現できる。[br][br][color=#0000ff][b]置換[br]→互いに素な巡回置換の積[br]→1要素共有互換の積の積[br]→任意の互換の積の積の積[br]→隣接互換の積の積の積の積[br][/b][/color][br]具体的にはよこ線の本数がものすごいことになってしまう。[br]しかし、理論的に可能だということが、今の段階では大切にしたいことだね。
[color=#0000ff][b](例)8本のあみだくじを互いに素な巡回置換の積で表そう。[br][/b][/color][math]\left(\begin{matrix}1,2,3,4,5,6,7,8\\3,6,4,1,5,8,2,7\end{matrix}\right)[/math][br]上を始点、下を終点の→でつなぐ、→の終点が別の→の始点になるものをさがして→を連結しよう。[br]1→3→4→1 から、(1 3 4)の巡回、2→6→8→7→2から、(2 6 8 7 ) の巡回、5→5から、(5)の巡回。[br][b](1 3 4) (2 6 8 7) (5)[/b][br][br][color=#0000ff][b](例)巡回置換(2 6 8 10)を互換で表そう。[br][/b][/color]2→6が1番目だから(2 6),10→2が最後にくる(2 10)。[br]6→2→8にすると6→8になるから、2番めは2→8にくるから(2 8)[br]8→2→10にするには(2 8)のあとは(2 10)で、これが3番目。右から互換を順にならべる。[br][b](2 10)(2 8)(2 6)[br][/b][br][color=#0000ff][b](例)互換(2 7)を1との互換の積で表そう。[br][/b][/color]2と7が1を経由して入れ替わるためには[br]2→1→7[br] 7→1→2[br]のように、[b](1 2)(1 7)(1 2)[/b]とすればよい。[br]7と2は対等なので、[b](1 7)(1 2)(1 7)[/b]でもできるはず。[br][br][color=#0000ff][b](例)互換(1 5)を隣接互換の積で表そう。[br][/b][/color]1→5は1→2→3→4→5で[br]5→1は5→4→3→2→1で実現できる。[br]しかし、2,3,4はもとに戻す必要がある。[br]1→5は1→2→3→4→5で[br]5→1は 5→4→3→2→1で[br]2→2は2→1 1→2で[br]3→3は 3→2 2→3で[br]4→4は 4→3 3→4で[br]実現できる。先にやる互換を右にかく。左右対称で、中央に(4 5)がくる。[br][b](1 2)(2 3)(3 4)(4 5)(3 4)(2 3)(2 1)[br][/b][br][color=#0000ff][b](例)3次の置換はどれも、2つの互換b=(1 2)と巡回置換s=(1 2 3)の積を使って表せる?[br][/b][/color]s[sup]3[/sup]=e, b[sup]2[/sup]=eだから、[b]e[/b]ができる。[br]言い換えると、s[sup]-1[/sup]=s[sup]2[/sup], b[sup]-1[/sup]=b[br]s[sup]-1[/sup]=[b](1 3 2)[/b][br]b s[sup]-1[/sup]=[b](1 2)(1 3 2)=(1 3)[/b][br]s b s[sup]-1[/sup]=[b](1 2 3)(1 3)=(2 3)[/b][br]これで、3つの互換と2つ巡回置換と恒等置換eが表現できた。[br]ぜんぶで6個の置換を表すことがでできた。3次の置換は3!=6個だからすべて作ることができる。
++記号の演習
[size=150][b]<数学の抽象化は概念化と切り離せない>[br][/b][/size][br]数学の抽象化は概念化、[br]つまり「用語と記号」の「約束」の世界だ。[br]群の「約束記号と用語」になれるために確認をしたい人はどうぞ。[br][br]「[color=#0000ff]群表[/color]」群の要素どうしの演算結果を九九表のように行列表にしたものを[br]「[color=#0000ff]ラテン方陣[/color]」群表はどの行にも演算結果が1回づつ漏れも重複もなく並ぶ。この特徴をもつ表のこと。[br]「[color=#0000ff][b]巡回群[/b][/color]」[b]巡回置換とはちがう[/b]。同じ巡回でも置換は群の1要素だが、巡回群は条件を満たす要素の集合。[br][b]1つの要素gを0乗からn−1乗まですると、その群の全要素n個がすべてならぶ群のこと。[br]gを[color=#0000ff]生成元[/color](generator)という。nを群の[color=#0000ff]位数[/color]という。[br][/b]C={e=g[sup]0[/sup],g[sup]1[/sup],g[sup]2[/sup],g[sup]3[/sup],.....,g[sup]n-1[/sup]}のように、巡回群Gではジェネレーターをgとすると、Gの要素は、[br]gのk乗としてえ指数表現できる。もちろん、演算を乗算に限る必要はないから加法群であっても[br]指数表現したりすることもあるね。[br][b][color=#0000ff]ジェネレーターがgの群を<g>とかくこともよくある。[br][/color][/b]「[color=#0000ff]群の位数(order)と要素の位数[/color]」位数nの群の各要素はn乗でeになるが、[br] nより小さいm乗でeになるyもある。mをyの位数という。[br] 群Gの位数は、集合のザイズでもあるから、[b]|G|[/b]とかくこともできる。[br] プログラミングのように、length(G),len(G)とかいても伝わる。[b]#G[/b]と書くことがよくある。[br] [color=#0000ff][b][size=150]mはnの約数になる。[br][/size][/b][/color](例)位数6の巡回群=C6={e=g[sup]6[/sup],g,g[sup]2[/sup],g[sup]3[/sup],g[sup]4[/sup],g[sup]5[/sup]}={e,g,a,b,c,d}としよう。[br] g[sup]6[/sup]=e,(g[sup]2[/sup])[sup]3[/sup]=e, (g[sup]3[/sup])[sup]2[/sup]=e,(g[sup]4[/sup])[sup]3[/sup]=e,(g[sup]5[/sup])[sup]6[/sup]=eとなるから、g,a,b,c,dの位数は6の約数で6,3,2,3,6になるね。[br][br][color=#9900ff][b][u][size=150]質問:位数6の巡回群をコードを使って作るにはどうしたらよいでしょうか。[br][/size][/u][/b][/color][br]6本のあみだは単位元e=[1],生成元g=[1,2,3,4,5,6]とすると、gを累乗するごとにgとは異なる別の要素ができて、6乗するとeになるはず。[br]リストgをami2dicで辞書にしてから、べき乗を計算する。[br]Gのn乗関数pow(G,n)を作るには、gの要素を1つずつ増やした辞書のリストを作り、polymultiRにgを入れるよう。中のgの個数n個だけかけ算するので、g^nを計算した結果の辞書を返してくれるでしょう。[br]逆元がそれぞれに一意に対応するから、群になることは明らかだね。[br]また、pow(G,n)の計算結果を、たとえば0乗から19乗までpgという名前のリストに入れておくと、[br]enumerateで、一気に計算結果を表示したり、pg[3],pg[12]のようにべき乗の結果を辞書で表示できますね。[br][br][color=#0000ff][IN]Python[br]#=====================================[br][b]def pow(G,n):[br] return polymultiR([ G for x in range(1,n+1)]) if n>0 else {1:1} [br] [br]g=[1,2,3,4,5,6][br]pg=[pow(ami2dic(g),index) for index in range(20)][br][br][/b]for i,value in enumerate(pg):[br] print(f"g^{str(i)}={value}")[br]print(pg[3])[br]print(pg[12])[br][b]#=====================================[br][/b][/color][OUT][br]g^0={1: 1}[br]g^1={1: 2, 2: 3, 3: 4, 4: 5, 5: 6, 6: 1}[br]g^2={1: 3, 2: 4, 3: 5, 4: 6, 5: 1, 6: 2}[br]g^3={1: 4, 2: 5, 3: 6, 4: 1, 5: 2, 6: 3}[br]g^4={1: 5, 2: 6, 3: 1, 4: 2, 5: 3, 6: 4}[br]g^5={1: 6, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}[br]g^6={1: 1}[br]g^7={1: 2, 2: 3, 3: 4, 4: 5, 5: 6, 6: 1}[br]g^8={1: 3, 2: 4, 3: 5, 4: 6, 5: 1, 6: 2}[br]g^9={1: 4, 2: 5, 3: 6, 4: 1, 5: 2, 6: 3}[br]g^10={1: 5, 2: 6, 3: 1, 4: 2, 5: 3, 6: 4}[br]g^11={1: 6, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}[br]g^12={1: 1}[br]g^13={1: 2, 2: 3, 3: 4, 4: 5, 5: 6, 6: 1}[br]g^14={1: 3, 2: 4, 3: 5, 4: 6, 5: 1, 6: 2}[br]g^15={1: 4, 2: 5, 3: 6, 4: 1, 5: 2, 6: 3}[br]g^16={1: 5, 2: 6, 3: 1, 4: 2, 5: 3, 6: 4}[br]g^17={1: 6, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}[br]g^18={1: 1}[br]g^19={1: 2, 2: 3, 3: 4, 4: 5, 5: 6, 6: 1}[br]{1: 4, 2: 5, 3: 6, 4: 1, 5: 2, 6: 3}[br]{1: 1}[br]
さらに、g^n=eだから、要素pの逆元g^(-1)=g^(n-1)です。[br]Gの位数n=6ならば、生成元gの逆元はpg(5)のはずです。[br]だから、pg[5]*pg[1]=eになるはず。[br][color=#0000ff][IN]python[br]#====================================[br]conL(pg[5],pg[1])[br][/color]#====================================[br][OUT][br]{1: 1}[br][br]巡回群の指数による周期性を使えば、剰余系と同じなので、[br]指数が負の指定があれば群の位数をたして正になるようにすればよいね。[br][IN]python[br]#====================================[br][b][color=#0000ff]def pow(G,n):[br] return polymultiR([ G for x in range(1,n+1)]) if n>0 else {1:1}[br]g=ami2dic([1,2,3,4,5,6])[br]def np(g,n):[br] if n>=0:[br] return pow(g,n)[br] else:[br] return np(g,n+len(g))[br][/color][/b]print(np(g,1))[br]print(np(g,3))[br]print(np(g,-1))[br]print(np(g,-30))[br]#=====================================[br][OUT][br]{1: 2, 2: 3, 3: 4, 4: 5, 5: 6, 6: 1}[br]{1: 4, 2: 5, 3: 6, 4: 1, 5: 2, 6: 3}[br]{1: 6, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}[br]{1: 1}[br]これで、逆元を求めることがー1乗の指定で求めることができるようになったね。