(draft) Special Lines and Centres of triangles

Arthur Lee, May 1, 2024

Special Lines and Centres of Triangles

Table of Contents

  1. soft construction exploration
    1. Circumcircle of a triangle (Soft Construction)
    2. Incircle of a triangle
    3. Trisecting a Triangle
  2. special lines
    1. triangle fold
    2. bisector of a triangle
    3. River excursion
  3. miscellaneous
    1. Special Lines & Centres of Triangles 三角形的特殊線和中心
    2. perpendicular bisectors
    3. where perpendicular bisectors intersect
    4. perpendicular bisectors and angles
    5. 6 mid-points
  4. 3D
    1. dumpling model
    2. Tetrahedron Net (general)
  5. more online resources
    1. orthocentre coordinates
    2. Centres of data / triangles

1.

soft construction exploration

This section suggests some exploratory tasks based on the concept of 'soft construction'. You may find out more from another collection by Anthony Or: https://www.geogebra.org/m/VytTQugN including his article: Or, A. C. M. (2013). Designing tasks to foster operative apprehension for visualization and reasoning in dynamic geometry environment. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 89–98), Oxford, UK. Available from https://hal.science/hal-00834054v3

  • 1. Circumcircle of a triangle (Soft Construction)
  • 2. Incircle of a triangle
  • 3. Trisecting a Triangle

1.1.

Circumcircle of a triangle (Soft Construction)

([i]Drag the three vertices of the triangle to change its shape.[/i])[br][br]Drag the blue point to A.[br]Drag the centre (the red point) to different positions at which the circle also passes through B.[br]Observe the marks of these positions. What are their characteristic?[br][br]What is the charateristic of the positions of the centre at which the circle passes through A and C?[br][br]How to draw the circle which passes thorough A, B and C?
Anthony Or. GeoGebra Institute of Hong Kong.
– Anthony OR 柯志明

1.2.

–

1.3.

–

2.

special lines

This section focuses on the meaning and properties of special lines (particularly those bisectors) related to a triangle (or part of a triangle). The 'river excursion' task is part of a collection about Voronoi Partitioning: https://www.geogebra.org/m/Ff6ZJdux

  • 1. triangle fold
  • 2. bisector of a triangle
  • 3. River excursion

2.1.

triangle fold

This is a triangle folding activity.[br][br]A and B are movable points. You can make a fold by dragging point C. Turn off the grid if needed. [br][br]What tasks or questions will you try for exploring properties of a triangle?
How about trying these:[br][list][*]make a fold to:[br][/*][/list] bisect angle A; angle B[br] bisect side BC; AC[br] add the altitude from A; from B[br][list][*]does the angle bisector of A bisect BC? when?[/*][*]show that longer side is opposite to greater angle[/*][*][size=100]cover point A, drag B to make angles B and C almost equal, fold C to B and compare the angles in order to tell which opposite side is longer[/size][br][/*][/list]
– Arthur Lee

2.2.

–

2.3.

–

3.

miscellaneous

  • 1. Special Lines & Centres of Triangles 三角形的特殊線和中心
  • 2. perpendicular bisectors
  • 3. where perpendicular bisectors intersect
  • 4. perpendicular bisectors and angles
  • 5. 6 mid-points

3.1.

Special Lines & Centres of Triangles 三角形的特殊線和中心

問題
[list=1][*]顯示三角形ABC的中線和形心G。量度AG和GA’。它們有甚麼關係？[br]類似地，BG和GB’、CG和GC’有甚麼關係？[/*][*]量度三角形AGB’和其餘五個三角形的面積(要先用多方形工具構作該六個三角形)。[br]它們有甚麼關係？[br][/*][*]顯示三角形ABC的垂直平分線和外心O。量度OA、OB及OC的長度。它們有甚麼關係？[br]嘗試以O為圓心繪畫一個圓形通過A、B及C(該圓稱為三角形ABC的[b]外接圓[/b])。[br][/*][*]顯示三角形ABC的角平分線及內心I。由I作垂直線到三角形ABC的三邊。量度I與三點垂足的距離。它們有甚麼關係？[br]嘗試以I為圓心繪畫一個圓形使它相切於三角形ABC的三邊(該圓稱為三角形ABC的[b]內接圓[/b])。[br][/*][*]顯示三角形ABC的四個中心(但隱藏各特殊線)和格線。[br]當ABC為[i]等腰[/i]三角形時，G、H、O和I有何特徵？[br][/*][*]當ABC為[i]直角[/i]三角形時，H和O有何特徵？[br][/*][*]當ABC為[i]鈍角[/i]三角形時，H和O有何特徵？[br][/*][*]甚麼情況下G、H、O和I會重合？[br][/*][*]G、H、O和I四者中，哪三者永遠共線(在同一直線之上)？它們之間的距離又有甚麼關係？[/*][/list]
gMath 互動數學教室[br][url=http://www.gmath.hk]http://www.gmath.hk[/url]
– Alex CHIK

3.2.

–

3.3.

–

3.4.

–

3.5.

–

4.

3D

This section shows some examples about special lines and triangle centres in 3-dimensional space.

  • 1. dumpling model
  • 2. Tetrahedron Net (general)

4.1.

dumpling model

This is a rice dumpling model in the shape of a tetrahedron with 4 faces of isosceles triangles. In the 3D model on the right, you may drag D, E and F to fold faces. [br][br]Imagine where the faces will meet. Make a guess and use the checkboxes to find out more about the shape.
If you drag C on the left, the 4 triangles will be changed but remains congruent. How would you describe, in general, which point on the plane will be the projection of the apex? [br][br]Check another version where the faces can be changed individually:[br]https://www.geogebra.org/m/hdgmkgsa [br][br]or this version, focusing on its apex and altitude:[br]https://www.geogebra.org/m/wdkbbq49
– Arthur Lee

4.2.

–

5.

more online resources

  • 1. orthocentre coordinates
  • 2. Centres of data / triangles

5.1.

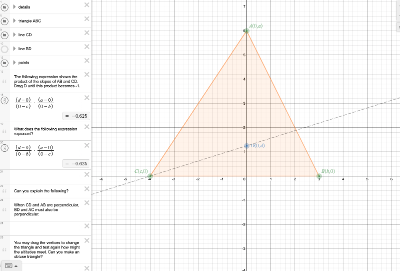
orthocentre coordinates

The property of altitudes and orthocenter can be studied easily in the coordinate plane. [br][br]Here is an example using Desmos calculator:[br][url=https://www.desmos.com/calculator/qrkzyjvdli]https://www.desmos.com/calculator/qrkzyjvdli[/url]
– Arthur Lee

5.2.

–

Information