Due semirette con la stessa origine dividono il piano in due regioni. Solitamente una è convessa e l'altra è concava. Queste due parti sono chiamate [b]angoli[/b]

Gli angoli si possono indicare in vari modi:[br][list][*]lato-origine-lato [math]\angle aOb[/math] [/*][*]punto-origine-punto [math]\angle COD[/math][/*][*]con una lettera greca [math]\angle\alpha[/math][/*][*]se non c'è ambiguità solo l'origine [math]\angle O[/math][/*][*]se non c'è ambiguità solo i lati [math]\angle ab[/math][/*][/list][br]

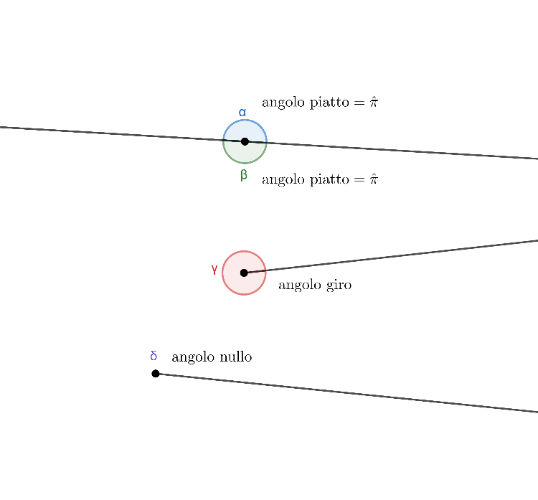
[list][*]se le due semirette che formano un angolo sono opposte, l'[b]angolo[/b] si dice [b]piatto[/b].[/*][*]se sono coincidenti posso considerare tutto il piano; e lo chiamo [b]angolo giro[/b][/*][*]oppure se sono coincidenti e l'angolo non contiene punti, lo chiamo [b]angolo nullo[/b][/*][/list]

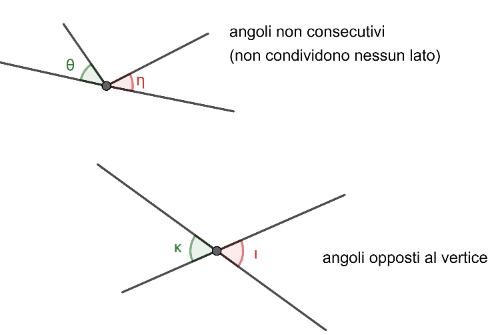
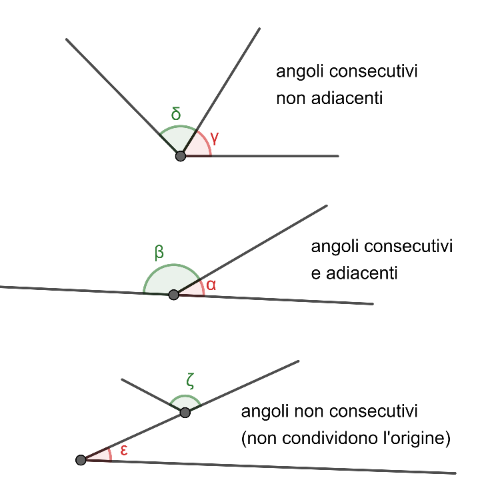
In modo simile ai segmenti, chiamiamo [b]angoli consecutivi[/b] quelle coppie di angoli che condividono un lato e l'origine. Se oltre ad essere consecutivi hanno i lati sulla stessa retta, allora li chiamiamo [b]angoli adiacenti[/b].

Chiamiamo [b]angoli opposti al vertice[/b], le coppie di angoli convessi che hanno i lati che sono i prolungamenti gli uni degli altri; cioè sono contenuti nella stessa retta.