Funktionsuntersuchung von künstlichen neuronalen Netzen
Künstliche neuronale Netze sind mathematische Funktionen. In diesem Buch wird ein Beispielnetzwerk Stück für Stück einer Funktionsuntersuchung unterzogen. Dabei können Erkenntnisse über die Funktionsweise, Chancen und Grenzen und das Generalisierungsvermögen von künstlichen neuronalen Netzen erarbeitet werden.
Table of Contents
- Das Netzwerk als mathematische Funktion
- Ein einzelner Knoten
- Das Netzwerk als Verkettung von Funktionen
- Parametereinfluss auf das gesamte Netzwerk
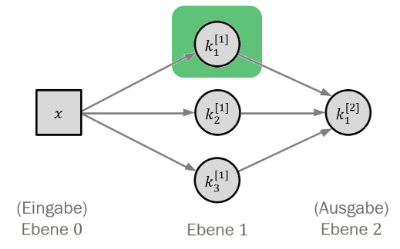
Ein einzelner Knoten
Willkommen zu diesem interaktiven Lernmodul! Nachdem eure Lehrkraft euch eine Einführung in Künstliche Neuronale Netze (KNNs) gegeben hat, wollen wir uns nun den grundlegendsten Baustein genauer anschauen: [b]einen einzelnen Knoten[/b] (auch Neuron genannt). Wir werden erforschen, wie ein solcher Knoten mathematisch beschrieben werden kann und welche Eigenschaften er hat.
Die Funktion eines Knotens
Stell dir vor, ein Knoten in einem neuronalen Netz erhält einen einzelnen Eingangswert, nennen wir ihn [math]x[/math]. Der Knoten verarbeitet diesen Wert und gibt einen neuen Wert aus. Diese Verarbeitung geschieht durch eine mathematische Funktion. Für unsere Untersuchung verwenden wir eine typische Funktion, die in einfachen KNNs vorkommt:[br][size=100][size=150][size=200][math]k(x)=σ(w⋅x+b)=\frac{1}{1+e^{-\left(w\cdot x+b\right)}}[/math][/size][br][/size][br]Dabei sind:[br][list][*][math]x[/math]: Der Eingangswert.[/*][*][math]w[/math]: Ein Parameter, genannt [b]Gewicht[/b] (englisch: weight). Er bestimmt, wie stark der Einfluss des Eingangswert [math]x[/math] ist.[/*][*][math]b[/math]: Ein weiterer Parameter, genannt [b]Bias[/b]. Er kann den Graphen der Funktion verschieben.[/*][*][math]σ[/math]: Die [b]Sigmoid-Funktion[/b], eine sogenannte [b]Aktivierungsfunktion[/b]. Meistens handelt es sich hierbei um nichtlineare Funktionen (wie das Beispiel). [br][br][/*][/list][b]Ziel[/b]: Wir wollen diese Funktion [math]k(x)[/math] wie eine normale Funktion aus dem Mathematikunterricht untersuchen (Definitionsbereich, Wertebereich, Verhalten für [math]x→\pm∞[/math], Monotonie, Extremstellen) und verstehen, wie die Parameter [math]w[/math] und [math]b[/math] ihren Graphen beeinflussen.[/size]
Definitionsbereich
Welche Werte darfst du für [math]x[/math] in die Funktion [math]k(x)=\frac{1}{1+e^{-\left(w\cdot x+b\right)}}[/math] einsetzen? Begründe deine Antwort.
Die innere lineare Funktion
Betrachten wir zuerst den Teil [math]w⋅x+b[/math] in der Klammer. Das ist eine lineare Funktion, die wir [math]L(x)[/math] nennen können.[br][br]Betrachte den folgenden Graphen der Funktion [math]L[/math]. Dies sollte dir bekannt vorkommen. [br]Bearbeite dabei folgende Aufträge:[br][list][*]Beschreibe die Veränderung des Graphens von [math]L[/math], wenn du den Wert von [math]b[/math] veränderst.[/*][*]Beschreibe die Veränderung des Graphens von [math]L[/math], wenn du den Wert von [math]w[/math] veränderst (probiere positive und negative Werte sowie [math]w=0[/math] aus).[/*][*]Nenne alternative Naben für [math]w[/math] und [math]b[/math] bei linearen Funktionen.[/*][/list]
Graph der Funktion L
Die Aktivierungsfunktion – Die Sigmoid-Funktion σ(z)
Die Sigmoid-Funktion ist definiert als [math]σ(z)=\frac{1}{1+e^{-x}}[/math]. [sup][/sup] Sie ist ein wichtiger Bestandteil vieler neuronaler Netze.[br][br]Betrachte den Graphen der Funktion [math]\sigma[/math]. Versuche dabei folgende Aufträge zu bearbeiten:[br][list=1][*]Bestimme den Wert von [math]\sigma\left(0\right)[/math].[/*][*]Bestimme den Wertebereich der Funktion.[/*][*]Bestimme das Verhalten des Graphens für [math]z\rightarrow\infty[/math].[/*][*]Bestimme das Verhalten des Graphens für [math]z\rightarrow-\infty[/math].[/*][*]Bestimme anhand des Graphens das Monotonieverhalten der Funktion (steigend oder fallend).[/*][*]Untersuche die Funktion anhand des Graphens auf Extremstellen. [/*][/list][br][i]Tipp: Du kannst den Punkte auf dem Graphen verschieben. [/i]
Der Graph der Funktion Sigma
Die Zusammengesetze Funktion
Jetzt setzen wir alles zusammen! Unten siehst du den Graphen der zusammengesetzten Funktion [math]k\left(x\right)=\sigma\left(L\left(x\right)\right)=\sigma\left(w\cdot x+b\right)=\frac{1}{1+e^{-\left(w\cdot x+b\right)}}[/math].[br][br]Betrachte den Graphen der Funktion [math]k[/math]. Bearbeite dabei folgende Arbeitsaufträge:[br][list][*]Verändere zunächst nur [math]b[/math] und beschreibe den Einfluss auf den Graphen von [math]k[/math].[/*][*]Setze [math]b=0[/math] und verändere nur [math]w[/math]. Beschreibe die Veränderung für [math]w>0[/math] und die Veränderung für [math]w<0[/math] und die besondere Situation mit [math]w=0[/math].[/*][/list]
Graph der Funktion k
Bearbeite folgende Aufträge basierend auf deinen Beobachtungen und dem Wissen über den Wertebereich der Sigmoid-Funktion: [br][br][b]Grenzverhalten:[/b][br][list][*]Bestimme den Wertebereich W der Funktion [math]k[/math] (wenn [math]w\ne0[/math])[/*][*]Beschreibe das Verhalten von [math]k\left(x\right)[/math] für [math]x\rightarrow\infty[/math] wenn [math]w>0[/math] oder wenn [math]w<0[/math] ist.[/*][*]Beschreibe das Verhalten von [math]k\left(x\right)[/math] für [math]x\rightarrow-\infty[/math] wenn [math]w>0[/math] oder wenn [math]w<0[/math] ist.[/*][*]Beschreibe das Verhalten von [math]k(x)[/math] für [math]x\rightarrow\infty[/math] wenn [math]w=0[/math].[/*][/list][br][b]Monotonie:[/b] [br][list][*]Bestimme, für welche Werte von [math]w[/math] ist die Funktion [math]k(x[/math]) streng monoton steigend / fallend ist.[/*][*]Untersuche die Monotonie für [math]w=0[/math].[/*][/list][b]Extremstellen:[/b][br][list][*]Untersuche die Funktion [math]k(x)[/math] (für [math]w\ne0[/math]) auf Extremstellen. Begründe deine Antwort anhand deiner Beobachtungen.[/*][/list]