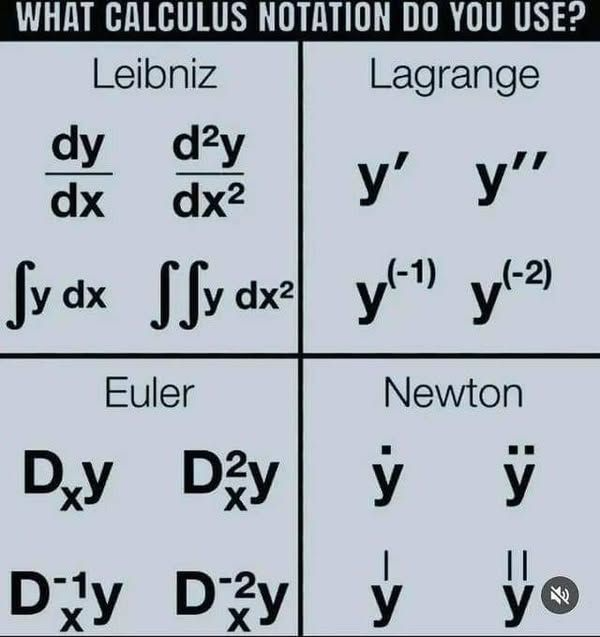
Differenzial und Integral
[size=150]In der Differenzialrechnung wird zu einer gegebenen Funktion die Ableitung bestimmt.[br]Hat man nun umgekehrt eine Funktion f(x), die Ableitung einer anderen Funktion y sein soll, also f = dy/dx, so fragt man nach ursprünglichen Funktion, also nach der Stammfunktion von f.[br]Aus dem Differenzialquotienten dy/dx = f(x) erhalten wir im Leibniz Calculus das Differential dy = f[math]\cdot[/math]dx. [br]Integrieren auf beiden Seiten ergibt[math]\int[/math]dy =[math]\int[/math]f(x) dx und dann y =[math]\int[/math]f(x) dx.[br]Hier wird offensichtlich, dass die Integration die Umkehrung der Differenziation ist. Der Hauptsatz wird zur Selbstverständlichkeit.[br][br]Siehe Lambacher-Schweizer (1950): Analysis. S. 131.[br][br]Die Notation von Leibniz erwies sich als intuitiv und genial.[br]Weitere Calculus Notationen: [/size]