Mechanika
Tabla de Contenidos
- Alapfoalmak
- Az ívmérték és a radián szemléltetése másolata
- Vektorműveletek másolata
- Vektorok a térben
- Vektorok felbontása merőleges összetevőkre másolata
- Vektoriális szorzat másolata
- Kinematika
- Hajítás 1.
- Hajítás 2
- Egyenes vonalú egyenletes mozgás
- Egyenesvonalu egyenletes mozgás 2
- Találkozás másolata
- Utolérés másolata
- Mozgó testek közötti legkisebb távolság
- Lejtőn mozgó test vizsgálata másolata
- Galilei-lejtő
- Sebesség-idő kvíz másolata
- Nyomképelemzés – Szabadesés, hajítás másolata
- Szabadesés vizsgálata mobiltelefonnal másolata
- Szabadesés a Marson, a Holdon, … másolata
- A körmozgás vizsgálata 1. másolata
- A körmozgás vizsgálata 2. másolata
- A körmozgás vizsgálata 4. másolata
- Buborék mozgása Mikola-csőben – Videoelemzés másolata
- Fékút
- Gyorsulás fogalmának bevezetése 2. másolata
- A gyorsulás fogalmának bevezetése 1. másolata
- Gyorsulás fogalmának bevezetése 2. másolata
- Dinamika
- A nehézségi gyorsulás változása a tengerszint feletti magassággal másolata
- A nehézségi erő elméleti meghatározása másolata
- Sztatika
- A súlyerő felbontása
- Rezgések és hullámok
- A harmonikus rezgőmozgás és a körmozgás kapcsolata
- Szabad és kényszer rezgések - Netfirms
- Az inga mozgásának vizsgálata másolata
- A harmonikus rezgőmozgás energiaviszonyai 1.
- A harmonikus rezgőmozgás energiaviszonyai 2. másolata
- Csillapodó rezgés vizsgálata másolata
- Ingaóra a Marson, a Holdon, … másolata
- Mechanikai kényszerrezgés másolata
- Azonos irányú rezgések összegzése, lebegés másolata
- Párhuzamos rezgések összeadása
- Fáziskülönbség - Netfirms
- Egymásra merőleges szinuszrezgések összegzése másolata
- Merőleges rezgések összeadása másolata
- Fourier tétele – Rezgések felbontása harmonikus rezgések összegére másolata
- Vonalmenti hullámok visszaverődése másolata
- Fázissebesség és csoportsebesség másolata
- Cunami másolata
- Transzverzális és longitudinális hullám
- Keresztirányú hullám - Netfirms
- Longitudinális hullám (Longitudinal wave) másolata
- Hosszanti hullám - Netfirms
- Doppler-effektus másolata
- Vízhullámok másolata
- A vízhullámok interferenciája - Netfirms
- Hullámok diffrakciója (akadály) - Netfirms
- Hullámok diffrakciója résen - Netfirms
- A hullámmozgás szemléltetése szimulációval
- Állóhullámok generálása húron - Netfirms
- Pontsoron terjedő hullámok interferenciája másolata
- Doppler effektus másolata
- Állóhullámok a kör alakú rezgő hártyán másolata
- Négyszög alakú rezgő hártyán kialakuló állóhullámok másolata
- Hangszin - Netfirms
- Hang lebegés (Acoustic Beats) - Netfirms
Az ívmérték és a radián szemléltetése másolata
[justify]Azt vizsgáljuk, hogy egy körben a sugárral egyenlő hosszúságú ívhez mekkora középponti szög tartozik, valamint a kör sugara hogyan viszonyul a kör kerületéhez.[/justify]
[justify]Mekkora középponti szög tartozhat egy körben egy olyan ívhez, amelynek hossza megegyezik a kör sugarával?[/justify]A rajzlapon egy animáció segítségével tudjuk a kör sugarát összemérni a kör kerületével. Játszd le az animációt és figyeld meg mi történik! Egészen addig folytasd, amíg a középponti szög el nem éri a teljes szöget (az A pont leírja az egész kört).[br][br]
Az animáció lejátszása után nyomd meg a kék színű gombot ([icon]/images/ggb/geomatech/info_bg.png[/icon])!
A „Magyarázat” jelölőnégyzet bejelölésével részletes magyarázatot kaphatsz.
[justify]Válaszolj a kérdésekre! A válaszokhoz használd a csúszkát, hogy beállítsd a kérdéses[br]szögeket! Miután válaszoltál, ellenőrizz ([icon]/images/ggb/geomatech/ellenőriz_bg.png[/icon])![/justify]
[justify]Ha egy szöget jól adtál meg ellenőrzéskor zöld pipa ([icon]/images/ggb/geomatech/helyes-inverz.png[/icon]) jelenik meg. Ha nem jó választ adtál piros x ([icon]/images/ggb/geomatech/helytelen-inverz.png[/icon]), ekkor nyomd meg a javítás gombot ([icon]/images/ggb/geomatech/figyelem_bg.png[/icon]) és módosítsd a válaszodat![/justify]
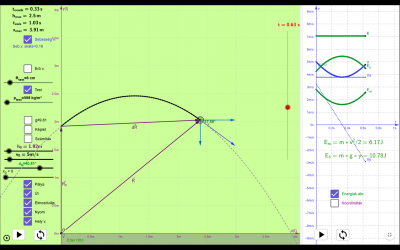
Hajítás 1.
[justify] Egy labda (kulcscsomó) elhajításának megfigyelése után, a GeoGebra alkalmazással részletesen megfigyelhetőek a kétdimenziós mozgás jellemzői. Érthetővé válik a [b]pálya[/b], az [b]út[/b], a [b]helyvektor[/b], [b]elmozdulás vektor[/b] fogalma. Megfigyelhető a sebesség két komponensének változása a mozgás során és ezeknek időbeli változása a jobboldali rajzlapon. Kipipálva (kattintással) az [b]Energia ábr[/b]ázolás négyzetét (gombját), követhető a test energiájának változása, a mozgás ideje alatt. A kezdeti feltételek a csúszkákkal változtathatóak. A [b]g[/b] gomra kattintva, változtatható a gravitációs gyorsulás értéke. A koordináta tengelyek léptékei automatikusan változnak.[/justify]
A nehézségi gyorsulás változása a tengerszint feletti magassággal másolata
[size=100][justify][color=#666666]A szimuláció segítségével megvizsgálhatod a nehézségi gyorsulás magasságfüggését.[/color][/justify][/size]
1. feladat
[color=#666666][size=100][justify]Fogd meg az egereddel a Föld felszínén található testet és változtasd a helyét! Milyen irányokban tudod mozgatni a testet és mit tapasztalsz minden esetben?[br][/justify][/size][/color]
2. feladat
[size=100][justify][color=#666666]Mozgasd a testet a Föld felszínén (tengerszinten), nem változtatva a magasságán! [br][br]a) Mitől függ a nehézségi gyorsulás a Föld felszínén?[br][br]b) Mit tapasztaltál, a Föld felszínén hol a legnagyobb és hol a legkisebb a nehézségi gyorsulás nagysága? Add is meg ezeken a helyeken az értékét![/color][/justify][/size]
3. feladat
[size=100][justify][color=#666666]Mozgasd a testet sugárirányban, a felszíntől való távolságot változtatva, valamelyik szaggatott vonal mentén! Mit tapasztalsz: egy adott szélességi fokon mitől és hogyan függ a nehézségi gyorsulás értéke?[/color][/justify][/size]
4. feladat
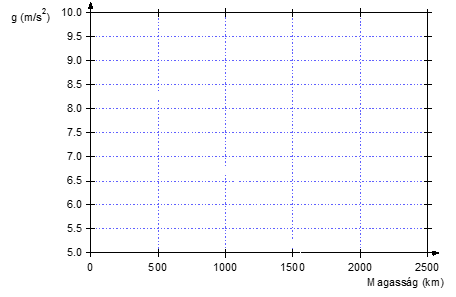
[size=100][justify][color=#666666]Az animációban az adott szélességi fokon a test felszíntől való távolságát változtatva olvasd le a megfelelő értékeket és készítsd el a test nehézségi gyorsulás ([i]g[/i]) - Magasság grafikonjait[br][br]a) az Egyenlítőnél! (0°)[br][br][/color][color=#666666]b) a Déli-sarkon! (D.SZ.90°)[br][br][/color][color=#666666]c) az Északi-sarkon! (É.SZ.90°)[br][/color][/justify][/size][justify][/justify]
5. feladat
[size=100][justify][color=#666666]Vizsgáld meg a kapott grafikonokat![br][br]a) Milyen függvényt kapsz, ha összekötöd a kapott pontokat?[br][br]b) Olvasd le a grafikonról: A Föld felszíne fölött kb. milyen magasságban lesz a szabadesés gyorsulása a szokásos érték háromnegyede?[/color][/justify][/size]
Kapcsolódó érdekességek
[justify][font=Calibri][font=Arial][color=#000000][/color][/font][/font][/justify][size=100][justify][font=Calibri][font=Arial][color=#666666]Eötvös Loránd a nehézségi gyorsulás (erő) helyi változásainak mérésére rendkívüli érzékenységű műszert szerkesztett és pontos mérési eljárást dolgozott ki. Torziós ingája egy platina - irídium szálon függő alumínium rúd, két végén egy-egy azonos tömegű platina hengerrel. Ebből az egyik henger drótszálra van függesztve, így egy kicsit mélyebben fekszik, mint a másik. Mivel a nehézségi erőtér inhomogén ([math]\vec{g}[/math][/color][/font][/font][font=Arial][color=#666666] a két henger helyén kissé különböző irányú és nagyságú), így a torziós szálra forgatónyomaték hat, az inga elfordul. A többféle irányba beállított inga helyzeteiből (elfordulási szögeiből) lehet kikövetkeztetni a nehézségi erő helyi változásait.[br][/color][/font][color=#666666]Eötvös Loránd ingája nem csak a nehézségi erő helyi változásainak felderítésére adott módot, hanem arra is, hogy a testek súlyos és tehetetlen tömegének azonosságát bebizonyítsa. (Egy test gyorsítása során fellépő tehetetlenség mértékét a tehetetlen tömeg jellemzi. A gravitációs kölcsönhatásban egy testet jellemző tömeget súlyos tömegnek nevezzük.)[br][/color][/justify][/size]
Közvetlen előismeret
[size=100][color=#666666]A nehézségi gyorsulás magasságfüggése (ha a tömegvonzási erőhöz képest kicsiny centrifugális erőtől eltekintünk) a tengerszint felett [i]h[/i] magasságban:[br][/color][/size][color=#666666][center][/center][center][math]g(h)=g_0(\frac{R}{R+h})^2=g_0\frac{1}{(1+\frac{h}{R})^2}[/math][/center][justify]ahol [i]g[/i][sub]0[/sub] az adott szélességi körön, a tengerszinten mérhető nehézségi gyorsulás. [/justify]Értéke:[br][/color][center][color=#666666][br][math]g_0=9,78\frac{m}{s^2}·(1+5,28·10^{-2}sin^2φ-5,9·10^{-6}sin^22φ)[/math][/color][color=#666666][br][/color][color=#666666][color=#666666] [/color][/color][/center][color=#666666][color=#666666] [/color][br]ahol [i]φ[/i] a földrajzi szélesség. [br][br]Ha [i]h[/i] << [i]R[/i], akkor[br][/color][center][color=#666666][br][math]g(h)\approx g_0\frac{1}{1+\frac{2h}{R}}\approx g_0(1-\frac{2h}{R})[/math][br][/color][br][/center][color=#666666][br]Távolodva a Földtől, a test egyre kevésbé érzi a Föld erőterét. Elvben persze a Földtől ható tömegvonzási erő csak a végtelenben tűnik el, de ha elég távol megyünk, akkor már más égitestek (például a Nap) vonzó hatása lesz a meghatározóbb, nagyobb.[br][/color]
Továbbhaladási lehetőségek
Az [url=http://tananyag.geomatech.hu/b/c5ElmJhr#]Ingaóra[/url] és a [url=http://tananyag.geomatech.hu/b/Bv85yjTp#]Szabadesés[/url] tananyagegységekben tanulmányozhatjuk a nehézségi gyorsulás értékét más égitesteken is.[br]
A súlyerő felbontása
Három esetben vizsgáljuk a elfüggesztett test súlyának felbontását két összetevőre.[br][br]Az alakzatok változtathatóak a kék pontok vonszolásával. A felfüggesztett test súlya (G) a csúszkával módosítható.
1. Konzol
2. Két végén rögzített kötél
3. Kötél és merev rúd
A harmonikus rezgőmozgás és a körmozgás kapcsolata
Figyeld meg a képet! [br]Milyen mozgást végez az óriáskerék egy kabinja különböző irányokból nézve? [br]A szimuláció segítségével megvizsgálhatod a két mozgás kapcsolatát.
1. feladat
Nézd meg figyelmesen a két mozgást! Milyen hasonlóság figyelhető meg köztük?
2. feladat
Figyeld meg a két test helyzetét! [br]Próbálj meg összefüggést keresni a két test függőleges kitérése között!
3. feladat
Hasonlítsd össze a két testre ható erőket![br]Figyeld meg, hogyan változik a körmozgást végző testre ható erő függőleges komponense!
4. feladat
Hasonlítsd össze a két test gyorsulását![br]Figyeld meg, hogyan változik a körmozgást végző test gyorsulásának függőleges komponense!
5. feladat
Hasonlítsd össze a két test sebességét![br]Figyeld meg, hogyan változik a körmozgást végző test sebességének függőleges komponense!
6. feladat
Próbáld meg észrevételeidet matematikai formában is megfogalmazni! [br]Az eredményeket leellenőrizheted, ha elolvasod az Elméleti hátteret. [br]Vesd össze eredményeidet a rezgőmozgás kitérés-idő, sebesség-idő és gyorsulás-idő grafikonjaival!
7. feladat
Változtasd a körmozgás frekvenciáját, sugarát és tömegét![br] Fogalmazd meg, hogyan változik a rezgőmozgás amplitúdója és frekvenciája!
Elméleti háttér
Minden harmonikus rezgőmozgáshoz található olyan egyenletes körmozgás, amelynek keringési ideje egyenlő a rezgésidővel, a pálya sugara egyenlő a rezgés maximális kitérésével (amplitúdó). Ezt a körmozgást referencia-körmozgásnak nevezzük. A referenciakör segítségével megadhatók a harmonikus rezgőmozgást leíró mennyiségek![br][br]A harmonikus rezgőmozgás kitérés-idő függvénye:[br][img]https://cdn.geogebra.org/resource/L4hdGxzb/xZG3RffJbbrYMKcM/material-L4hdGxzb.png[/img][br][br]A harmonikus rezgőmozgás kitérés-idő függvénye: [math]y(t)=r\cdot sin\varphi=A·sin\varphi[/math][br]Felhasználva az egyenletes körmozgás szögelfordulása és szögsebessége közötti [math]\varphi=ω\cdot t[/math] összefüggést: [math]y(t)=A·sinωt[/math].[br]A két mozgás frekvenciája és periódusideje megegyezik, így [math]\omega=\frac{2\pi}{T}=2\pi\cdot f[/math].[br][math]ω[/math] a rezgőmozgás körfrekvenciája. A harmonikus rezgőmozgás körfrekvenciája egyenlő az egyenletes körmozgás szögsebességével.[br]A harmonikus rezgőmozgás sebesség-idő függvénye:[br][img]https://cdn.geogebra.org/resource/FSR3RrCK/MVonGUq88R24PGuj/material-FSR3RrCK.png[/img][br]Az ábra alapján: [i][math]v(t)=v_k\cdot cos\varphi=v_k\cdot cosωt[/math][/i][br]Az egyenleteskörmozgás sebessége: [math]v_k=r\cdotω=A\cdotω[/math][br]Behelyettesítve: [b][math]v(t)=A\cdotω\cdot cosωt[/math][/b][br][br]A harmonikus rezgőmozgás gyorsulás-idő függvénye:[br][img]https://cdn.geogebra.org/resource/WaJj11BT/ghmzeXSZbKbQXZVj/material-WaJj11BT.png[/img][br]Az ábra alapján: [math]a(t)=-a_{cp}\cdot sin\varphi=-a_{cp}\cdot sinωt[/math][br]A gyorsulás előjele negatív, mert ellentétes irányú a kitéréssel. [br]Az egyenletes körmozgás gyorsulása: [math]a_{cp}=r\cdotω^2=A\cdotω^2[/math][sup][br][/sup]Behelyettesítve: [b][math]a(t)=-A\cdotω^2\cdot sinωt[/math][/b][br][br][br]