Geogebra Book Materi Kelas 7 dan 8 SMP
Book ini dirancang untuk membantu peserta didik memahami berbagai konsep matematika kelas 8 secara interaktif dan menyenangkan. Dalam materi statistika, siswa dapat memvisualisasikan data melalui tabel, serta menghitung rata-rata, median, dan modus. Pada materi geometri, hubungan antar sudut dalam segitiga dan garis sejajar dieksplorasi secara dinamis, didukung dengan pembuktian teorema Pythagoras menggunakan representasi visual. Sistem Persamaan Linear Satu Variabel (SPLSV) juga dipelajari melalui grafik dan metode aljabar, memudahkan peserta didik memahami solusi secara nyata. Selain itu, book ini mengajarkan perbandingan melalui aktivitas interaktif, serta melibatkan visualisasi model 3D untuk memahami volume balok dan kubus. Dengan pendekatan berbasis teknologi, GeoGebra Book ini memungkinkan peserta didik belajar secara mandiri dan mendalam melalui eksplorasi konsep-konsep matematika yang relevan dengan kehidupan sehari-hari.
Sisällysluettelo
- PERBANDINGAN SUDUT
- Materi Sudut Sehadap
- Sudut Sehadap
- Sudut Bertolak Belakang
- Materi Sudut Bertolak Belakang
- SOLUSI SISTEM PERSAMAAN LINEAR SATU VARIABEL
- Materi Solusi Persamaan Linear Satu Variabel
- Solusi Sistem Persamaan Linear Satu Variabel
- TEOREMA PYTHAGORAS
- Materi Teorema Pythagoras
- Pembuktian Teorema Pythagoras
- PERBANDINGAN
- Materi Perbandingan
- Perbandingan (Rasio)
- VOLUME BALOK DAN KUBUS
- Materi Volume Kubus dan Balok
- Volume Kubus dan Balok
Materi Sudut Sehadap
Tujuan Pembelajaran
1. Siswa dapat memahami pengertian sudut sehadap pada dua garis sejajar yang dipotong oleh garis transversal.[br]2. Siswa dapat mengidentifikasi pasangan sudut sehadap pada suatu diagram atau gambar.[br]3. Siswa dapat menggunakan konsep sudut sehadap untuk menyelesaikan permasalahan geometri.
Sudut Sehadap
[b]Pengertian Sudut Sehadap[/b][br][list][*]Sudut sehadap adalah pasangan sudut yang terbentuk ketika dua garis sejajar dipotong oleh sebuah garis transversal.[/*][*]Pasangan sudut ini terletak di posisi yang "sehadap" atau "sama arah" pada masing-masing garis sejajar.[/*][/list][b]Ciri-ciri Sudut Sehadap[/b][br][list=1][*]Sudut-sudut tersebut berada di sisi yang sama dari garis transversal.[/*][*]Posisi sudut berada di tempat yang "sehadap" atau "sama arah" pada garis sejajar.[/*][*]Jika kedua garis yang dipotong sejajar, besar sudut sehadap selalu sama.[/*][/list]
Video Pemahaman Sudut Sehadap
Video Pemahaman Sudut Sehadap
Materi Solusi Persamaan Linear Satu Variabel
Tujuan Pembelajaran
[list=1][*]Peserta didik dapat memahami pengertian dan bentuk umum Sistem Persamaan Linear Satu Variabel (SPLSV).[/*][*]Peserta didik dapat menyelesaikan SPLSV menggunakan metode substitusi, eliminasi, atau campuran.[/*][/list]
1. Pengertian SPLSV (Sistem Persamaan Linear Satu Variabel)
[size=100][b]Sistem Persamaan Linear Satu Variabel (SPLSV)[/b] adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan [math]\left(=\right)[/math] dan hanya mempunyai satu variabel berpangkat satu. Kalimat terbuka adalah kalimat yang belum dapat ditentukan nilai kebenarannya, bernilai benar saja atau salah saja karena memiliki unsur yang belum diketahui nilainya. Variabel adalah simbol/lambang yang mewakili sebarang anggota suatu himpunan semesta. Variabel biasanya dilambangkan dengan huruf kecil.[br][br]Bentuk umum persamaan linier satu variabel[br][math]ax+b=0[/math][br]dengan [math]a[/math] dan [math]b[/math] bilangan bulat bukan nol serta [math]x[/math] adalah variabel yang dicari.[/size]
2. Penyelesaian SPLSV
Penyelesaian SPLSV bertujuan mencari nilai [math]x[/math] yang membuat persamaan menjadi benar. Metode penyelesaian SPLSV antara lain:[br][b]a. Metode aljabar[/b], yakni dengan cara menyelesaikan persamaan secara manual dengan langkah-langkah aljabar. [br][b]b. Fisualisasi grafik[/b], dengan mewakili persamaan dalam bentuk grafik garis, kemudian mencari titik potong dengan sumbu [math]x[/math].
3. Penerpan SPLSV dalam Kehidupan Sehari-hari
Sistem Persamaan Linear Satu Variabel (SPLSV) sering digunakan untuk menyelesaikan berbagai masalah sehari-hari yang melibatkan hubungan linear antara dua atau lebih elemen. Berikut adalah beberapa contoh penerapannya:[br][list][*][b]Perhitungan keuangan, [/b]SPLSV membantu menghitung biaya atau menentukan harga barang.[/*][*][b]Perencanaan dan manajemen waktu,[/b] SPLSV dapat digunakan untuk menghitung waktu yang dibutuhkan dalam aktivitas.[/*][*][b]Pengelolaan produksi atau proyek,[/b] digunakan untuk menentukan jumlah bahan yang diperlukan dalam sebuah proyek.[/*][*][size=100]Dan masih banyak lagi.[/size][/*][/list]
4. Video Pemahaman SPLSV
Agar lebih memahami terkait materi SPLSV, lihatlah video berikut ini
SPLSV
Materi Teorema Pythagoras
Tujuan Pembelajaran
[list=1][*]Peserta didik dapat memahami dan membuktikan Teorema Pythagoras melalui visualisasi hubungan kuadrat sisi-sisi segitiga siku-siku.[/*][*]Peserta didik dapat menghitung panjang sisi segitiga siku-siku menggunakan Teorema Pythagoras.[/*][*]Peserta didik dapat mengidentifikasi tripel Pythagoras dan menggunakannya dalam menentukan panjang sisi segitiga siku-siku.[/*][/list]
2. Pembuktian Teorema Pythagoras
Pembuktian Teorema Pythagoras dapat dilakukan dengan:[br][list=1][*]Membuat segitiga siku-siku dengan sisi [math]a[/math],[math]b[/math], dan [math]c[/math].[/*][*]Gambarlah persegi pada setiap sisi segitiga.[/*][*]Bandingkan luas persegi di sisi miring ([math]c^2[/math]) dengan jumlah luas dua persegi di sisi lainnya ([math]a^2+b^2[/math]).[/*][*]Sehingga dapat disimpulkan bahwa luas persegi di sisi miring ([math]c^2[/math]) akan selalu sama dengan jumlah luas dua persegi lainnya ([math]a^2+b^2[/math]).[br][/*][/list]
1. Pengertian Pythagoras
Teorema Pythagoras menyatakan hubungan antara sisi-sisi segitiga siku-siku. Dalam segitiga siku-siku:[br][math]a^2+b^2=c^2[/math][br]di mana:[br][math]c[/math] adalah panjang sisi miring ([i]hipotenusa[/i]), yaitu sisi terpanjang yang berhadapan dengan sudut siku-siku.[br][br]
2. Menghitung Panjang Sisi dengan Teorema Pythagoras
Jika dua sisi dari segitiga siku-siku diketahui, panjang sisi ketiga dapat dihitung menggunakan rumus:[br][list=1][*][b]Jika sisi miring ([math]c[/math][/b][b]) dicari: [b] [/b][b][/b][math]c=\sqrt{a^2+b^2}[/math][br][/b][/*][*][b] Jika salah satu sisi siku-siku ([math]a[/math]atau [math]b[/math]) dicari: [math]a=\sqrt{c^2-b^2}[/math][/b][b][/b] atau [math]b=\sqrt{c^2-a^2}[/math][/*][/list][br]Contoh Soal:[br]Sebuah segitiga siku-siku memiliki sisi-sisi [math]a=6cm[/math] dan [math]b=8cm[/math], tentukan sisi miringnya ([math]c[/math])[br]Jawab:[br][math]c=\sqrt{a^2+b^2}[/math][br][math]c=\sqrt{6^2+8^2}[/math][br][math]c=\sqrt{36+64}[/math][br][math]c=\sqrt{100}[/math][br][math]c=10cm[/math]
3. Video Teorema Pythagoras
Untuk lebih memahami lebih dalam teorema pythagoras, maka tontonlah video berikut:
Materi Perbandingan
Tujuan Pembelajaran :
1. Peserta didik dapat menghubungkan konsep perbandingan dengan konteks nyata [br]2. Peserta didik dapat memahami penyelesaian masalah perbandingan dengan alat bantu interaktif secara mendalam [br]3. melatihpeserta didik dalam menggunakan alat digital untuk menyelesaikan masalah matematika praktis
A. Materi
Perbandingan adalah membandingkan dua atau lebih besaran yang sama dan ditunjukkan dengan nilai yang paling sederhana. Kita dapat menggunakan perbandingan atau rasio untuk membanadingkan besaran suatu benda dengan benda yang lain. Besaran benda yang dimaksud dapat berupa panjang, kecepatan, massa, waktu, jumlah benda, usia, dan sebagainya. [br]Hal-hal yang perlu diperhatikan untuk menyederhanakan perbandingan adalah :[br]1. Mempunyai besaran yang sama [br]2. Menunjukkan nilai terkecil atau paling sederhana dari nilai kedua sisi. (nilai kedua sisi merupakan bilangan asli)
B. Contoh Soal
Umur Ibu 45 tahun dan umur adik 15 tahun. Untuk membandingkan umur ibu dan adik dapat dilakukan dengan cara berikut :[br]a. Mencari selisih [br] Umur ibu 45 tahun dan umur adik 15 tahun, selisihnya 45 - 15 = 30 tahun[br]b. Mencari hasil bagi [br] Umur Ibu 45 tahun dan umur adik 15 tahun, maka hasil bagi = [math]\frac{45}{15}[/math] atau [math]45:15=3:1[/math]
C. Video Pemahaman Perbandingan
Materi Volume Kubus dan Balok
Tujuan Pembelajaran
1. Dapat mempermudah peserta didik dalam memvisualisasikan konsep Volume balok dan kubus melalui model 3D yang dapat diputar dan diubah dimensinya[br]2. Dapat meningkatkan pemahaman peserta didik mengenai hubungan dimensi dan volume melalui eksperimen mengubah panjang, lebar, dan tinggi
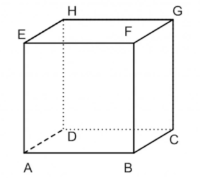
Kubus
A. Pengertian[br] Bangun ruang tiga dimensi yang tersusun dari 6 bidang datar yang kongruen, keenam bidang kongruen pada kubus berbentuk persegi.[br][br]B. Sifat-sifat kubus[br]1. Mempunyai 6 sisi yang sama besar berbentuk persegi[br]2. Mempunyai 12 sisi rusuk yang sama panjang[br]3. Mempunyai 8 buah titik sudut[br]4. Mempunyai 12 diagonal bidang[br]5. Mempunyai 4 diagonal ruang[br][br]C. Rumus Volume [br][math]V=s^3=s\cdot s\cdot s[/math][br]keterangan : v = volume[br] s = panjang sisi
Gambar Kubus
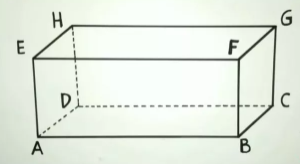
Balok
A. Pengertian[br]Balok adalah bangun ruang tiga dimensi yang yang tersusun oleh 3 pasang segiempat (persegi atau persegi panjang) dan paling sedikit mempunyai 1 pasang sisi segi empat yang mempunyai bentuk berbeda.[br][br]B. Sifat-sifat Balok[br]1. Balok tersusun dari 3 pasang sisi yang sama (total 6 buah sisi)[br]2. Setiap sisi berbentuk segiempat yaitu persegi atau persegi panjang[br]3. Paling sedikit harus mempunyai 1 pasang sisi dengan bentuk yang berbeda[br]4. Mempunyai 12 rusuk[br]5. Rusuk-rusuk yang sejajar mempunyai ukuran yang sama[br]6. Mempunyai 4 diagonal bidang [br]7. Diagonal bidang yang sejajar memiliki ukuran yang sama[br]8. Mempunyai 4 diagonal ruang dan semuanya mempunyai ukuran yang sama[br]9. Setiap bidang diagonal berbentuk persegi panjang.[br][br]C. Rumus Volume[br][math]V=p\cdot l\cdot t[/math][br]Keterangan : V = volume[br] p = panjang sisi[br] l = lebar[br] t = tinggi
