Kongruenzsätze
In diesem Geo-Gebra-Buch lernst du 1. was Kongruenz bedeutet 2. mit welchen Angaben sich ein Dreieck [b]eindeutig[/b] konstruieren lässt. (Kongruenzsätze) 3. die vier Kongruenzsätze, und wie sich zugehörige Dreiecke konstruiren lassen.
Índice
- Einführung Kongruenz
- Einführung Kongruenz
- Dreiecksfamilien
- seite, seite, (seite)
- seite, winkel, (seite)
- winkel, seite, (winkel)
- seite, seite, winkel
- Kongruenzsätze
- Zusammenfassung
- sss - Konstruktion
- wsw - Konstruktion
- sws - Konstruktion
- Ssw - Konstruktion
Einführung Kongruenz
Was bedeutet Kongruenz?
Zwei geometrische Figuren sind [b]kongruent[/b], wenn sie in Form und Flächeninhalt übereinstimmen. [br]Ein anderes Wort dafür ist [b]deckungsgleich[/b].[br]Das heißt: Wenn man man kongruente Figuren verschiebt, dreht oder spiegelt, dann passen sie genau übereinander.
Aufgabe 1
Überprüfe durch Verschieben und Drehen, ob die Dreiecke kongruent sind.[br]In welchen Dreiecken stimmen deine gefundenen kongruenten Dreiecke überein?
Welche Dreiecke sind Kongruent zueinander?
In welchen Größen stimmen die Dreiecke überein?
Aufgabe 2
[list][*]Überprüfe durch Messen der Seitenlängen und Winkel beider Dreiecke, ob die Dreiecke kongruent sind.[/*][*]Winkel misst du mit dem ersten Werkzeug, indem du im Uhrzeigersinn nacheinander die beiden Seiten am jeweiligen Winkel antippst.[/*][*]Seitenlängen misst du mit dem zweiten Werkzeug, indem du die zugehörige Seite antippst.[/*][*]Durch klicken auf neu, wird dir die nächste Figur angezeigt.[/*][/list]
seite, seite, (seite)
Wie viele verschiedene Dreiecke mit den Seiten [math]c=10cm[/math] und [math]b=5cm[/math] gibt es? [br]Wie viele Dreiecke gibt es, die zusätzlich die Seite [math]a=8cm[/math] haben?[br][br][i]Untersuche die Fragen mit folgendem Applet.[/i]
Wie viele Dreiecke haben die Seitenlängen [math]c=10cm[/math] und [math]b=5cm[/math]?
Wie viele Dreiecke haben die Seitenlängen [math]c=10cm[/math], [math]b=5cm[/math] und [math]a=8cm[/math]?
Wie viele Seiten müssen gegeben sein, damit man ein Dreieck eindeutig konstruieren kann?
Zusammenfassung
Vervollständige den folgenden Lückentext. Dieser fasst die Erkenntnisse aus den vorangegangenen Kapiteln zusammen.
Merkkasten zu Kongruenzsätzen
Wenn du den Lückentext richtig ausgefüllt hast, dann [b][u]übernimm folgenden Merkkasten in dein Heft:[/u][/b]
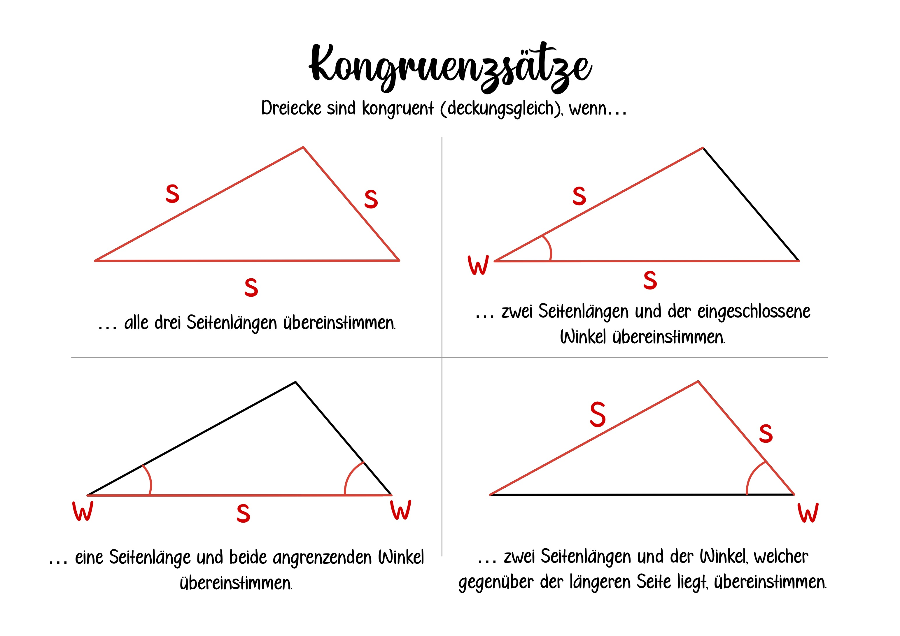
Kongruenzsätze erkennen
In der nachfolgenden Aufgabe werden verschiedene Dreiecke dargestellt. In jedem Dreieck sind drei Größen farblich markiert. Dies stellen die gegebenen Größen dar.[br]Ordne jedem Dreieck den passenden Kongruenzsatz zu.
Sind drei Größen gemäß einem der vier Kongruenzsätze gegeben, so lässt sich ein [b]Dreieck eindeutig konstruieren[/b]. Wie das funktioniert, wird in den nächsten Abschnitten erklärt.