Lerne GeoGebra 3D Rechner
Willkommen beim [url=https://www.geogebra.org/3d]GeoGebra 3D Rechner[/url]! Lerne mit Hilfe der folgenden Video-Anleitungen unter anderem wie du verschiedene Körper konstruierst, Rotationen oder Kegelschnitte visualisierst und sphärische Dreiecke zeichnest.
Table of Contents
- Erste Schritte
- Vergleich der GeoGebra Mathe Apps
- Einleitung
- Erforsche die App
- Algebra-Ansicht
- Werkzeug-Ansicht
- 3D Grafik-Ansicht
- Augmented Reality
- Grundlagen
- Zylinder und Würfel
- Modellieren in AR
- Rotationen
- Kegelschnitte
- Kreise in 3D
- Vertiefung
- Sphärische Dreiecke
- Quadratische Flächen - Quadriken
- Polyeder durch Spiegeln erstellen
- YouTube Anleitungen
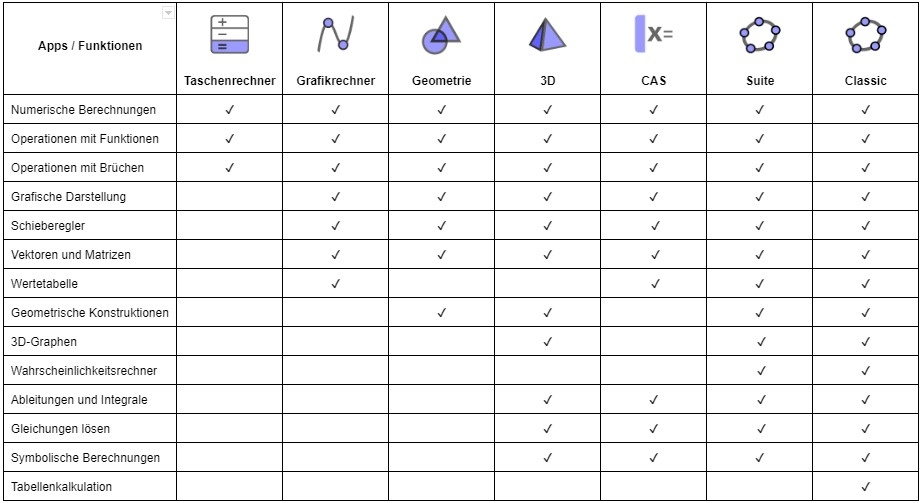
Vergleich der GeoGebra Mathe Apps
Mit unseren [i]GeoGebra Mathe Apps[/i] kannst du Funktionen, Geometrie, Algebra, Statistik und 3D auf eine neue und interaktive Weise erkunden und lernen.[br][list][*][url=http://www.geogebra.org/scientific]Taschenrechner[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafikrechner[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrie[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rechner Suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS Rechner[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Rechner[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]Die richtige App für dich ist die, die deinen eigenen Bedürfnissen entspricht und, wenn sie in Prüfungen verwendet wird, die Prüfungsbestimmungen für deine Region erfüllt. Die folgende Tabelle gibt einen Überblick darüber, welche Funktionen in welchen Apps verfügbar sind.
GeoGebra in Prüfungen
Wir glauben, dass die Schüler*innen davon profitieren, wenn sie im Unterricht, bei den Hausübungen und während Prüfungen genau dieselbe [i]GeoGebra [/i]App verwenden. Auf diese Weise erhalten sie die meiste Übung mit der App und können unsere Technologie daher in allen Situationen optimal nutzen. Aus diesem Grund haben wir unseren [i]GeoGebra Prüfungsmodus[/i] erstellt und ihn in jede unserer Apps eingefügt. Der [i]Prüfungsmodus [/i]sperrt mobile Geräte, sodass die Schüler*innen während einer Prüfung keine anderen Apps als [i]GeoGebra[/i] verwenden und mit diesen kommunizieren können. Dieser Ansatz wurde bereits von mehreren Bildungsministerien in mehreren Regionen erprobt und genehmigt. Erfahre mehr über die Verwendung von [url=https://www.geogebra.org/m/m97r7cd4][i]GeoGebra[/i] in Prüfungen[/url].[br][br]
Zylinder und Würfel
Aufgabe
Konstruiere einen Zylinder und einen Würfel. [br][br]Erforsche die folgende Konstruktion und lerne, wie du im [url=https://www.geogebra.org/3d]GeoGebra 3D Rechner[/url] einfache Körper konstruieren kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1. [/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Öffne die [i]Einstellungen[/i] und wähle [i]Koordinatengitter anzeigen. [/i][/td][/tr][tr][td]2.[/td][td][/td][td]Gib in der [i]Algebra-Ansicht[/i] den Befehl [math]Zylinder((2,-3,-1),(2,2,2),2)[/math] ein, um einen Zylinder durch zwei Punkte mit einem Radius von 2 zu erstellen und drücke die [i]Eingabetaste[/i]. [/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Erkunde verschiedene Projektionen, indem du sie in den Einstellungen änderst. [br][/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Wechsle in die [i]Werkzeug-Ansicht, [/i]wähle das [i]Punkt [/i]Werkzeug und erstelle zwei neue Punkte. [/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_cube.png[/icon][/td][td]Wähle das [i]Würfel [/i]Werkzeug und wähle die erstellten Punkte, um einen Würfel zu konstruieren. [/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Wähle das [i]Bewege [/i]Werkzeug und erkunde deine Konstruktion. [br][/td][/tr][/table]
Versuche es selbst...
Augmented Reality
Wenn du den [i]GeoGebra 3D Rechner[/i] auf einem mobilen Gerät verwendest, kannst du in den [i]AR[/i] [i]Modus [/i]wechseln, um deine erstellten mathematischen Objekte auf jeder ebenen Fläche (z.B. Tisch, Boden, ...) um dich herum zu platzieren und um sie herum zu gehen. Erkunde deine Konstruktionen aus einer neuen Perspektive!
Sphärische Dreiecke
Aufgabe
Erstelle ein Dreieck auf einer Kugel.[br][br]Erforsche die folgende Konstruktion und lerne, wie du im [url=https://www.geogebra.org/3d]GeoGebra 3D Rechner[/url] sphärische Dreiecke konstruieren kannst. Danach versuche es selbst, indem du die folgenden Anleitungen befolgst.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td][/td][td]Gib in der [i]Algebra-Ansicht[/i] [math]A=(0,0,0)[/math] und den Befehl [math]Kugel(A,1)[/math] in das [i]Eingabefeld[/i] ein. [/td][/tr][tr][td]2.[/td][td][/td][td]Wähle die Kugel in der [i]3D Grafik-Ansicht [/i]aus und wähle [img]https://wiki.geogebra.org/uploads/thumb/d/d5/Color_button.svg/16px-Color_button.svg.png[/img] [i]Farbe[/i] in der erscheinenden [i]Gestaltungsleiste[/i], um die Farbe der Kugel zu ändern.[br][/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Öffne die [i]Einstellungen [/i]und deaktiviere [i]Achsen anzeigen[/i] und [i]Ebene anzeigen[/i], um die Achsen und die Ebene auszublenden. [/td][/tr][tr][td]4.[/td][td][/td][td]Wechsle in die [i]Werkzeug-Ansicht.[/i][/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Wähle das [i]Punkt [/i]Werkzeug und erstelle auf der Kugel drei Punkte [i]B[/i], [i]C [/i]und [i]D.[/i][/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_circlearc3.png[/icon][/td][td]Verwende das [i]Kreisbogen[/i] Werkzeug und wähle als erstes den Mittelpunkt [i]A, [/i]dann [i]B [/i]und [i]C. [/i]Wiederhole diesen Schritt zweimal mit den anderen Punkten, um ein sphärisches Dreieck zu erstellen (wähle immer als erstes Punkt [i]A[/i] aus).[br][/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Verwende das [i]Bewege[/i] Werkzeug und ziehe an den Punkten auf der Kugel, um deine Konstruktion zu erkunden. [br][/td][/tr][/table]
Versuche es selbst...
Augmented Reality
Wenn du den GeoGebra 3D Rechner auf einem mobilen Gerät verwendest, kannst du in den AR Modus wechseln, um deine erstellten mathematischen Objekte auf jeder ebenen Fläche (z.B. Tisch, Boden, ...) um dich herum zu platzieren und um sie herum zu gehen. Erkunde deine Konstruktionen aus einer neuen Perspektive!