barycentric coordinates
The position of a point can be described using coordinates. In a cartesian coordinate system the position of a point can be calculated as a linear combination of unit vectors on the coordinate axes. In polar notation a point is defined by its distance to the origin and a rotation angle, measured starting from the x-axis. But these two systems are not the only possible ones. In triangles thousands of remarkable points, called triangle centers, can be identified. For these points it's useful to take the verticles of the triangle as a reference instead of unit vectors on the axes. These verticles unambigously define the so called barycentric coordinates of a point. In this GeoGebrabook you can learn more about these coordinates.
Inhaltsverzeichnis
- point and segment
- point on segment
- point and segment
- point and triangle
- barycentric coordinates
- bar. coord. and area
- bar. coord. by matrices
- matrices in CAS
- remarkable points
- equilateral triangle
- rectangular triangle
- center of gravity
- midpoint of incircle
- orthocenter
- circumcenter
- Kimberling numbers
point on segment
another system of coordinates
In a Oxy system of coordinates, a point C can be defined by a linear combination of unit vectors on the x-axis and the y-axis. [br]For a point C on a segment |AB| it's useful to define its position relatively to the ending points of the segment. Now Point Vectors to the ending Points A and B are used as unit vectors.[br]The new coordinates of C are defined by the weight of the lenghts of the segments in which C devides the segment |AB|. Therefore we call them [b]barycentric coordinates[/b].
barycentric coordinates
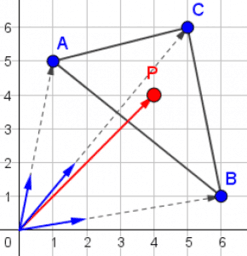
position relative to the verticles of a triangle
In a triangle ABC we can define the position of a point P relatively to the verticles of the triangle using Point Vectors to these verticles. These three vectors form the unit vectors of the barycentric coordinate system. Every point in the plane has got three coordinate numbers. We can calculate these coordinate numbers out of the cartesian coordinates of A, B, C and P.[br]Note that the sum of the coordinate numbers equals 1.
equilateral triangle
In an equilateral triangle the midpoints of the sides are marked. They define a new equilateral triangle. The centers of gravity of both triangles is the same.[br]Drag P in the triangle and look how these points have got remarcable barycentric coordinates.