Parcours Prof - Des incontournables
Il s'agit d'une ressource à destination des enseignants. Elle vise à reprendre des aspects importants pour l'enseignant, et qui représentent des potentiels forts de Geogebra. Ces éléments techniques s'adressent plus spécifiquement aux enseignants dans leur travail de production de ressource et de gestion de classe.
Table of Contents
- Multi - fenêtre
- Un premier exemple
- Un exemple plus élaboré
- Utiliser la fenêtre de calcul formel
- Utiliser des curseurs
- Un premier exemple d'utilisation de curseurs
- D'autres utilisation des curseurs
- Visualisation et présentation
- Une animation sympa
- Somme des angles aigus d'un triangle
- Volet 3D
- Premier pas - visualisons un prisme et une section
- Création d'autres supports : pavé droit et pyramide
- Un recueil de feuilles dynamiques auto-correctives
- Tirer profit d'un script autocorrectif
- Un script clé en main
- Problème de rebond au billard
- Exercice Auto Correctif Vierge
- Pour aller plus loin dans les scripts et l'usage de booléens
- Personnaliser les outils à disposition
- Menu < Outils >
- Personnaliser la barre d'outils
- Créer un nouvel outil (Macro)
- Sauvegarde et réutilisation des nouveaux outils
- Travailler en ligne
- Copie de Groupe et gestion : GGbBook pour tout expliquer
- Latex... faudrait pas oublier son potentiel
- Quelques usages de Latex avec Geogebra
Un premier exemple
Dans l'applet ci-dessous, on peut constater le lien entre les deux fenêtres (géométrie et tableur) en faisant bouger les points A, B et C[br]Exercice (voir vidéo ci-dessous si besoin) : [br] a) Faire calculer le rapport AC/AB dans la cellule B6 (il suffit de taper =AC/AB)[br] b) Faire afficher l'angle CBA en D6 (on peut utiliser directement la fonction Angle(Point,Point,Point) ou bien l'angle qui est déjà créé, il s'appelle [math]\beta[/math])[br] c) Faire afficher tan(CBA) en B7
Capsule vidéo pour la fabrication du fichier ci-dessus
Un premier exemple d'utilisation de curseurs
Dans l'appliquette ci-dessous :
- Bouger les curseurs a et b[br]- Animer les[br]- Changer la vitesses d'animation
Tutoriel création de curseur
Une animation sympa
Animation
Les objets mobiles de géogébra peuvent être animer très simplement, et tous les objets dépendant de cet objets s'animeront en conséquences. On peut ainsi créer des animations parfois plus démonstratives que le simple déplacement des objets à la souris (transformation du plan animées avec une vitesse plus ou moins grande, point décrivant une courbe, figure animée .....)
Protocole de construction
Lorsque une figure est créée, GGB enregistre automatiquement le protocole de construction. On pourra l'utiliser pour montrer rapidement aux élèves la construction pas à pas sans avoir à tout refaire devant eux.[br]>> voir la vidéo ci-dessous
le petit moulin
Maintenant à vous d'essayer de reproduire cette animation, vous pouvez pour cela visionner la vidéo ci-dessous ...
Premier pas - visualisons un prisme et une section
Voici un support pour visualiser une section et son évaluation en fonction du point mobile M
[u][b][size=200]Créons ce support pas à pas.[/size][/b][/u][br]C'est l'occasion de découvrir le volet de création 3D.[br]Très vite, il apparait que c'est un espace de travail pour le prof pour fournir des supports aux élèves. Cela constitue difficilement un objectif d'apprentissage pour ces derniers.
Ouverture du volet Géométrie 3D
Création et gestion des points libres
Mon premier solide : un prisme (évidemment!)
Toilettage pour préparer le support de visualisation
Manipuler le solide - vue 2D des sections
[b][size=200]Une synthèse pour finir ce premier aperçu du volet 3D[/size][/b]
Une version papier pour les premiers pas
Un script clé en main
Quelle est l'idée ?
Il est possible de créer des scripts sous Geogebra, c'est à dire des programmes qui s'exécuteront par clic, ou par actualisation. [br][br][b]En général :[/b][br]Chaque objet créé dispose dans ses [color=#999999][b]Propriétés[/b][/color] d'un volet [color=#999999][b]Script[/b][/color]. [br]Il s'agit soit de scripts Geogebra, soit de scripts en Javascript. Cela représente donc un potentiel intéressant, à condition d'avoir quelques compétences dans ces langages.[br][br][b]Avant un tel défi, adaptons une feuille avec le script clé en main :[/b][br]C'est tout l'intérêt du travail en ligne et de partager des ressources! [br]Nous allons utiliser un script clé en main et le personnaliser pour disposer et créer des feuilles dynamiques et [b]auto-correctives[/b]. [br]L'élève aura un bouton à sa disposition pour tester sa construction et se corriger sans une intervention systématique de l'enseignant. [br][br]Pour les plus avancés d'entre nous, une ressource plus complète est proposée en fin de rubrique pour explorer ce potentiel.
Capsule vidéo sur un exemple (le cercle circonscrit)
Processus de création
On exploite la ressource Geogebra disponible au dessous.[br]Pour être simplement retrouvée, elle est également donnée à la fin de cette rubrique (nous vous recommandons de la sauvegarder pour votre simplifier votre usage et enrichir vos ressources)[br][br]Comme expliqué pas à pas dans la vidéo, il s'agit :[br]- de préciser la construction, l'énoncé de cet exercice comme les données de départ (ici un triangle quelconque ABC) [br]- de personnaliser le script : spécifier les noms des objets à tester, pointer les "bonnes réponses"[br]- de cacher les traits de construction[br]- de personnaliser la barre d'outils pour que l'exercice ait un intérêt[br]
La feuille à personnaliser
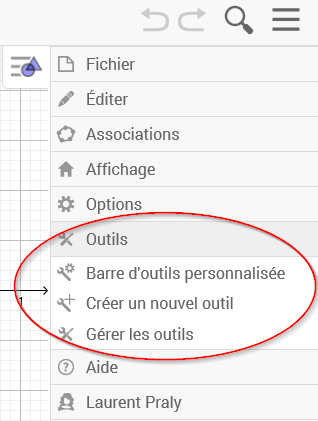
Menu < Outils >
On se concentre sur le menu [b][color=#999999]Outils[/color][/b] et l'intérêt qu'il peut représenter en classe pour proposer un travail différencié ou progressif[br][br]Les intitulés sont explicites :[br]-[b][color=#999999] Barre d'outils personnalisée[/color][/b] permet de sélectionner des outils dans la palette accessible par défaut.[br]Il est bien utile de priver l'élève de l'outil [icon]/images/ggb/toolbar/mode_circle3.png[/icon] lorsqu'on veut mobiliser son savoir-faire de construction du cercle circonscrit à un triangle.[br]- [b][color=#999999]Créer un nouvel outil[/color][/b]. C'est clair, mais il est bon de voir combien c'est simple![br]- [b][color=#999999]Gérer les outils [/color][/b]nous permettra de conserver et gérer les outils à disposition et ceux créés.
Copie de Groupe et gestion : GGbBook pour tout expliquer
[s]lien vers la ressource : [/s][url=https://ggbm.at/eYVesOMX]https://ggbm.at/eYVesOMX[/url] la ressource n'est plus accessible...[br][br]On pourra se documenter avec la version anglaise : https://www.geogebra.org/m/rQrbooeq
Quelques usages de Latex avec Geogebra
[size=200][color=#0000ff]Mettre en forme avec Latex le contenu d'une appliquette [br][/color][/size][b](i.e. une feuille dynamique Geogebra)[br][br]Tous les textes, mais aussi les légendes des objets créés peuvent être écrits en LateX.[/b][br]Il suffit d'embraser par des $ une expression et d'utiliser les notations LateX pour mettre tout en forme à l'intérieur.[br][br]Quelques exemples : [br][list][math]\frac{u_{n+1}}{u_n}[/math] s'écrit donc $\frac{u_(n+1)}{u_n}$[br][math]\overrightarrow{AB}[/math] s'écrit donc $\overrightarrow{AB}$[br][math]\sqrt{2\times\Pi}[/math] s'écrit donc $\sqrt{2\times\Pi}$[br][math]\widehat{ABC}[/math] s'écrit donc $\widehat{ABC}$[br][math]\left [p-1,96\times{\sqrt{\frac{p(1-p)}{n}}} ; p+1,96\times{\sqrt{\frac{p(1-p)}{n}}} \right ][/math] s'écrit donc $\left [p-1,96\times{\sqrt{\frac{p(1-p)}{n}}} ; p+1,96\times{\sqrt{\frac{p(1-p)}{n}}} \right ]$[/list][br]Bon pour ce dernier exemple, on cale un peu si on n'est pas un habitué de LateX.[br]Le site suivant vous sera alors bien utile pour composer votre syntaxe : [b][url=http://www.codecogs.com/latex/eqneditor.php]éditeur en ligne[/url][/b]
[color=#0000ff][size=200]Exporter une figure vers LateX[br][/size][/color][b][br]Vous souhaitez inclure une figure dans vos documents Latex[/b], mais c'est toujours pénible à rédiger.[br][br]C'est sans savoir que Geogebra vous propose directement l'export d'une figure sélectionnée en code LateX près à être inséré![br]Cela devient une simple formalité : une histoire de copier/coller
[size=150][color=#0000ff][size=200]Dans une feuille de travail en ligne[/size][/color][/size][br]Enfin, lorsque le travail est organisée sur une feuille de travail en ligne, l'éditeur de texte propose un outil de mise en forme de formule.[br][math]u_{n+1}=\frac{1}{2}u_n-12[/math] peut s'écrire comme en latex, mais encadré des balises ouvrantes [code][math][/code] et fermantes[code][/math][/code].
[size=200][color=#cc0000]Ecrire des formules dans des activités Geogebra[br][/color][/size][br]Il suffit d'embrasser les syntaxes LateX par la balise ouvrante [code][math][/code] et sa clôture [code][/math][/code].[br]On peut aussi utiliser l'assistant "insérer Maths" accessible depuis l'icône [i][b]f[/b][/i][sub][b]x[/b] [/sub]à gauche de l'encart de réponse.
[size=200][color=#cc0000]Veux-tu faire des essais?[/color][/size][br]Profite de l'encart en dessous pour écrire à l'aide des balises [code][math][/code] et [code][/math][/code][code][/code]