Fibonacci Sequence & Golden Ratio by Erin and Allison
Table of Contents
- Teacher Notes
- Goals
- Students - START HERE
- Fibonacci Sequence
- Golden Rectangles
- Constructing Golden Rectangles
- Graphing Golden Rectangles
- Golden Triangles
- Golden Triangles
- Pentagons and The Golden Ratio
- Extension
- The Golden Ratio in the World
- Fibonacci Music
Goals
Purpose
The purpose of this Geogebra book is to introduce students to the connections between the Fibonacci Sequence and the Golden Ratio through exploration with Golden Rectangles and Triangles.
Standards
[url=http://www.corestandards.org/Math/Content/HSG/CO/A/5/]CCSS.MATH.CONTENT.HSG.CO.A.5[/url][br]Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.[br][br][url=http://www.corestandards.org/Math/Content/HSG/SRT/A/2/]CCSS.MATH.CONTENT.HSG.SRT.A.2[/url][br]Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.[br][br][url=http://www.corestandards.org/Math/Content/HSS/ID/B/6/]CCSS.MATH.CONTENT.HSS.ID.B.6[/url][br]Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.[br][br][url=http://www.corestandards.org/Math/Content/HSS/ID/B/6/a/]CCSS.MATH.CONTENT.HSS.ID.B.6.A[/url][br]Fit a function to the data; use functions fitted to data to solve problems in the context of the data. Use given functions or choose a function suggested by the context. Emphasize linear, quadratic, and exponential models.[br][br][url=http://www.corestandards.org/Math/Content/HSS/ID/B/6/c/]CCSS.MATH.CONTENT.HSS.ID.B.6.C[/url][br]Fit a linear function for a scatter plot that suggests a linear association.[br][br][url=http://www.corestandards.org/Math/Content/HSS/ID/C/7/]CCSS.MATH.CONTENT.HSS.ID.C.7[/url][br]Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.
Objectives
Students will be able to ... [br]- identify the Fibonacci Sequence within the constructions of Golden Rectangles,[br]- connect the Fibonacci Sequence algebraically and graphically to the Golden Ratio through a linear model of best fit,[br]- recognize recursion through rotations and dilation within constructions of Golden Rectangles and Triangles,[br]- develop an "eye" for recognizing shapes that are "Golden,"[br]- and apply previously learn concepts about similarity.
Fibonacci Sequence
STOP watching at 1:50!!!
Constructing Golden Rectangles
1. Create a 1x1 square. *Use the regular polygon tool!* Create another 1x1 square and stack it to the right of the first 1x1 square. *Create the new square AWAY from the first square and then stack them together!*
What are the dimensions of the new rectangle formed by the two 1x1 squares? (Write your answer with the smaller dimension first and the larger dimension second.)
2. Create a new square from the longer side of the 1x2 rectangle and stack the new square below the 1x2 rectangle.
What are the dimensions of the newest rectangle formed by all of the squares?
3. Create a new square from the longer side of the 2x3 rectangle and stack the new square to the left of the 2x3 rectangle.
What are the dimensions of the newest rectangle formed by all of the squares?
4. Create a new square from the longer side of the 3x5 rectangle and stack the new square above the 3x5 rectangle.
What are the dimensions of the newest rectangle formed by all of the squares?
5. Create a new square from the longer side of the 5x8 rectangle and stack the new square to the right of the 5x8 rectangle.
What are the dimensions of the newest rectangle formed by all of the squares?
Make a prediction!
If you were to continue this construction pattern...[br]- What will the dimensions of the new square be?[br]- Where will you stack this new square?[br]- What will the dimensions of the newest rectangle be?
Make a generalization!
How do you know what the dimensions of the newest rectangle will be, based on the previous rectangle?
Make a connection!
How are the rectangles you created with the applet related to the Fibonacci Sequence from the Introduction?
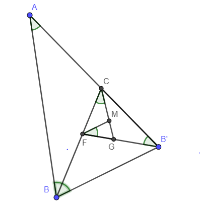
Golden Triangles
Create TRIANGLE 1
-Construct TRIANGLE 1 with 2 angles measuring 72 degrees and one angle measuring 36 degrees. [br]-Make sure to make the sides of TRIANGLE 1 line segments.[br]-Answer the questions below about TRIANGLE 1.
Create TRIANGLE 2
-Create a 36-degree angle counterclockwise about the left-hand base angle.[br]-Use a line to connect B with the point on the side of the 36-degree angle.[br]-Connect vertex B to the point of intersection of the side of the angle and side or original triangle.[br]-Answer questions about TRIANGLE 2.
Create TRIANGLES 3 an 4
-Repeat the process from Creating TRIANGLE 2 by constructing a 36-degree angle, counterclockwise about the left side base vertex.[br]-Make some guesses about TRIANGLES 3 and 4. Write the guesses under the TRIANGLES 3 and 4 section below. [br]-Confirm if your conjectures/guesses were correct. Explain how you did this below, too.
TRIANGLE 1
Write down at least 3 things that you notice about TRIANGLE 1.
TRIANGLE 1
Calculate the ratio of the length of one of the long sides of TRIANGLE 1 to the base length of TRIANGLE 1. [br][br] RT1 =
TRIANGLE 2
Calculate the ratio of the length of one of the long sides of TRIANGLE 2 and the base length of TRIANGLE 2.[br][br]RT2 =
TRIANGLE 2
What do you notice about TRIANGLE 1 and TRIANGLE 2?
Compare the length of the base of TRIANGLE 1 to the length of one of the longer sides of TRIANGLE 2. What do you notice?
TRIANGLES 3 and 4
Write down your conjectures/guesses about TRIANGLES 3 and 4.
How did you confirm or disprove your conjectures?
TRIANGLES 1, 2, 3, 4
Why are these called Golden Triangles?
TRIANGLES 1, 2, 3, 4
Write down three connections the you observe between the work you did with Golden Triangles and the work you with on the Golden Rectangles.
The Golden Ratio in the World
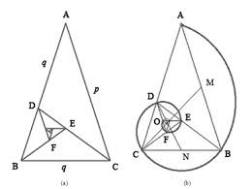
Describe how the Golden Ratio relates to this picture.
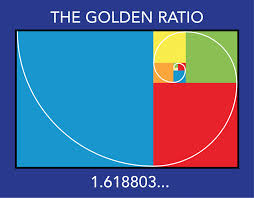
Describe how the Golden Ratio relates to this picture.
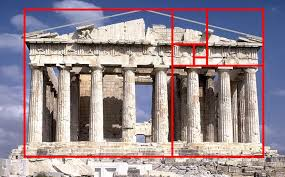
Describe how the Golden Ratio relates to this picture.
Describe how the Golden Ratio relates to this picture.
Describe how the Golden Ratio relates to this picture.
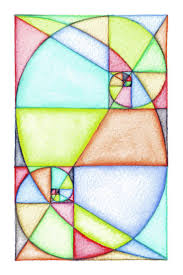
Describe how the Golden Ratio relates to this picture.
Describe how the Golden Ratio relates to this picture.