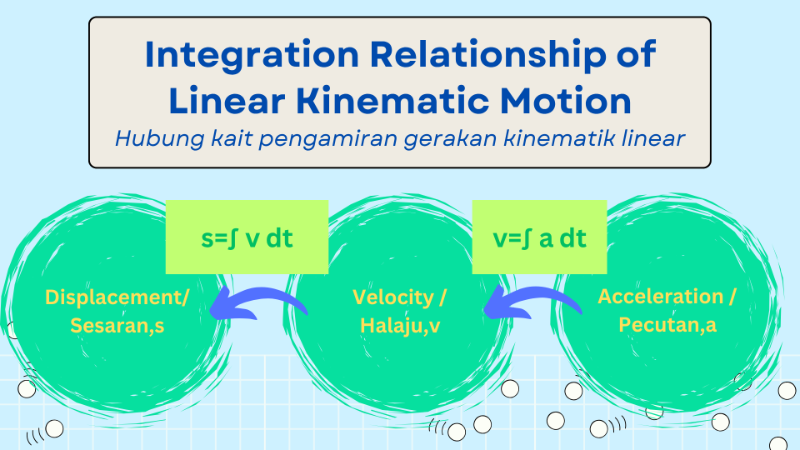
[justify]You had learnt the acceleration function, a of a particle that moves linearly can be obtained by differentiating the velocity function, v with respect to time. t, that is:[br] [math]a=\frac{dv}{dt}[/math][br][br]However, if the acceleration function, a, of a particle is given, how can we determine the velocity function,v of the particle?[br][br]When the acceleration function [math]a=\frac{dv}{dt}[/math], the velocity function, v can be determined by integrating the acceleration function, a with respect to time, t which is [math]v=\int a[/math]dt.[i][br][br][/i]In general, the relationship between acceleration function, a = h(t) and velocity function, v = g(t) can be simplified as follows:[br][/justify] [math]a=h\left(t\right)[/math] [math]\longrightarrow[/math] [math]v=\int adt[/math] [math]\longrightarrow[/math] [math]v=g\left(t\right)[/math]

[left]Given a velocity function, v, how can we determine the displacement, s, of the particle? How can we determine the velocity function, v, and alsoy the displacement function, s, of a particle from an acceleration function, a?[br][br]When the velocity function, v, is given as a function of time t, the displacement function, s, can be obtained by performing integration, which is:[br][br][br][b]s=∫ v dt[/b][br][br]and when the acceleration function, a, is given as a function of time t, the displacement function, s, can be obtained by performing two consecutive integrations, which are:[br][math]v=\int adt[/math], then follow by [math]s=\int vdt[/math][/left]