Parabeln parallel zur y-Achse strecken

Die Normalparabel wird durch die Funktionsvorschrift [math]y=x^2[/math] beschrieben. In dieser Aktivität sollst du untersuchen, wie sich die Parabel verändert, wenn [math]x^2[/math] noch mit einer positiven Zahl multipliziert wird. Also zum Beispiel: [br][math]y=2x^2[/math][br][math]y=\frac{1}{4}x^2[/math][br]oder[br][math]y=0,1x^2[/math][br][br]Allgemein werden diese Parabeln mit der Gleichung [math]y=a\cdot x^2[/math]angegeben.

Untersuche den Verlauf des Graphen f mithilfe des Schiebereglers.

Der Graph [math]f[/math] wird durch die Gleichung [math]y=a\cdot x^2[/math] beschrieben. Es gilt erst einmal: [math]1\le a\le10[/math]. [br][br]Vergleiche den Verlauf mit der Normalparabel: Kreuze die richtigen Aussagen an.

Je größer a, desto offener/weiter verläuft der Graph in positiver y-Richtung. Je größer a, desto schmaler/enger verläuft der Graph in positiver y-Richtung. Für [math]a=10[/math] entspricht der Graph der Normalparabel. Für [math]a=1[/math] entspricht der Graph der Normalparabel.

Mit diesem Wissen kannst du Graphen auch Funktionsvorschriften zuordnen.

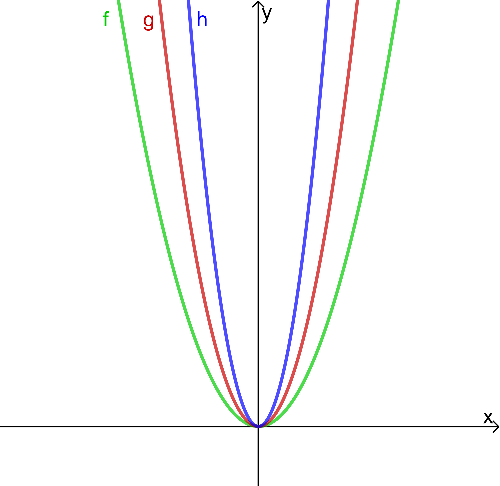
Oh nein, da hat jemand am Koordinationensystem die Skala an der x- und y-Achse vergessen.

Welche Funktionsgleichungen könnten zu den Graphen passen? Kreuze mögliche Kombinationen an.

[math]f:y=2x^2,g:y=3x^2[/math] und [math]h:y=4x^2[/math] [math]f:y=3x^2,g:y=2x^2[/math] und [math]h:y=x^2[/math] [math]f:y=x^2,g:y=3x^2[/math] und [math]h:y=2x^2[/math] [math]f:y=x^2,g:y=3x^2[/math] und [math]h:y=5x^2[/math]

Jetzt wird a kleiner...

Als nächstes sollst du den Verlauf des Graphen für [math]a\le1[/math] untersuchen. [math]a[/math] bleibt aber positiv.

Untersuche noch einmal den Verlauf des Graphen f mithilfe des Schiebereglers.

Der Graph [math]f[/math] wird durch die Gleichung [math]y=a\cdot x^2[/math] beschrieben. Es gilt aber dieses Mal [math]a\le1[/math], aber immer noch positiv. [br][br]Vergleiche den Verlauf mit der Normalparabel: Kreuze die richtigen Aussagen an.

Je größer a, desto offener/weiter verläuft der Graph in positiver y-Richtung. Je größer a, desto schmaler/enger verläuft der Graph in positiver y-Richtung. Für [math]a=\frac{1}{2}[/math] entspricht der Graph der Normalparabel. Für [math]a=0[/math] wäre der Graph keine Parabel mehr. Für [math]a=1[/math] entspricht der Graph der Normalparabel. Das wird langsam alt.

Und wieder hat jemand die Skalen am Koordinatensystem vergessen... :-)

In der Klassenarbeit gäbe das aber Abzug.

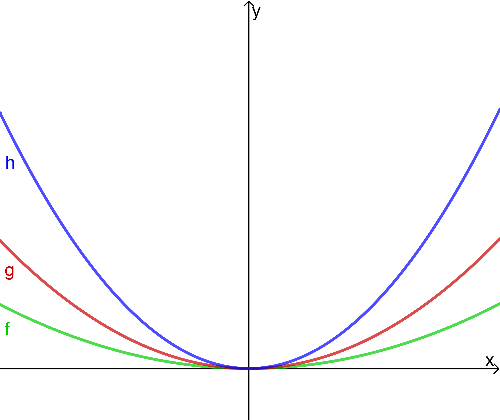
Welche Funktionsgleichungen könnten zu den Graphen passen? Kreuze mögliche Kombinationen an.

[math]f:y=0,001x^2,g:y=0,01x^2[/math] und [math]h:y=0,1x^2[/math] [math]f:y=0,1x^2,g:y=0,2x^2[/math] und [math]h:y=0,3x^2[/math] [math]f:y=\frac{1}{4}x^2,g:y=\frac{1}{3}x^2[/math] und [math]h:y=\frac{1}{2}x^2[/math] [math]f:y=\frac{1}{2}x^2,g:y=\frac{1}{3}x^2[/math] und [math]h:y=\frac{1}{4}4x^2[/math]

Zusammenfassung

Der Graph [math]f[/math] einer Parabel wird durch die Gleichung [math]y=a\cdot x^2[/math] beschrieben. [math]a[/math] ist eine beliebige positive Zahl und wird als [b][u]Streckfaktor [/u][/b]bezeichnet. [br][br]Kreuze die richtigen Aussagen an.

Für [math]a=1[/math] entspricht der Graph der Normalparabel. Je kleiner [math]a[/math], desto weiter verläuft der Graph in positiver y-Richtung. Je größer a, desto schmaler/enger verläuft der Graph in positiver y-Richtung. Je kleiner [math]a[/math], desto enger verläuft der Graph in positiver y-Richtung. Je größer a, desto offener/weiter verläuft der Graph in positiver y-Richtung. Für [math]a[/math] muss gelten: [math]a\ne0[/math]. Wenn [math]a[/math] kleiner als 1 ist, dann ist der Graph im Vergleich zur Normalparabel weiter. Wenn [math]a[/math] größer als 1 ist, dann ist der Graph im Vergleich zur Normalparabel enger.