Motivation
[justify]The motivation to create this GGB book arises from the exploration of the possible ways to introduce technology in the classroom to motivate students and to make a proper use of technology in class.[br] [br]3D printings are here to stay and making a good use of such resources in class can be motivating for students but also may improve the understanding of certain topics. [br][br]At the start when I first wanted to 3d print form GeoGebra I found a lot of difficulties due to the fact that the only tutorial I found was: [url=https://www.geogebra.org/m/pjbms8sy]https://www.geogebra.org/m/pjbms8sy[/url] it explains how to export to STL files and have several examples but when I tried to create my own files I found myself with zero-thickens objects and things that could not be recognized in the STL files or in the 3d printing software. [br][br]In this book I am adding the solutions to the problems I found and some didactic approach from a teacher's point of view that I hope is of use if you want to try this ideas in class. [br][br]I am sure that any average GeoGebra user is able of finding it's own way to do this but as I spent a lot of time revising forums and asking questions I am trying to make it easier for other users to create significant advances and not spend so much time figuring this our. [/justify][br]
Rotating functions
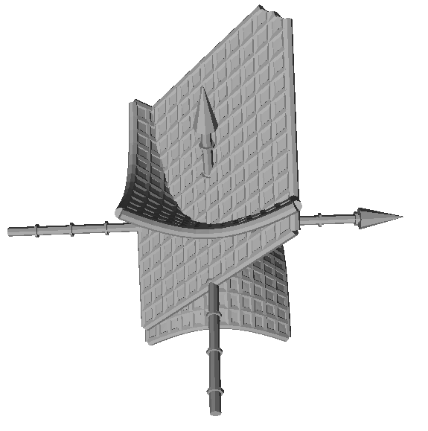
The first way I found to export to an STL file is rotating a function on the x axis.[br][br]In this applet a building was modeled. We can model any object of our interest and rotate 360° it in the x axis to create a solid of revolution. [br][br]In this applet the building I used is: 30 St Mary Axe (The Gherkin) [url=https://en.wikipedia.org/wiki/30_St_Mary_Axe]https://en.wikipedia.org/wiki/30_St_Mary_Axe[/url]
This kind of activities allow us to work:[br][br][list][*]Functions[/*][*]Modelling[/*][*]Algebra[/*][*]Solids of revolution[/*][*]Integrals (volumes of revolution)[/*][/list]
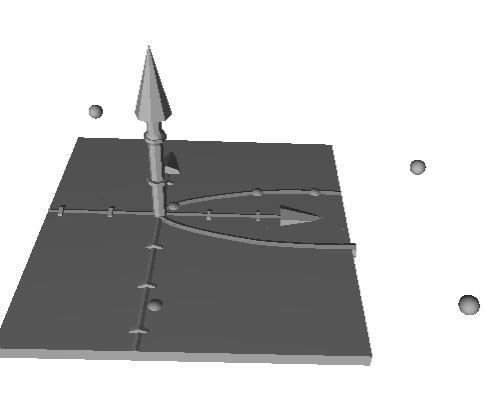
The problem I found is that when I tried to export this to STL I could only export the axis, the trace of the functions are not exported in STL because a trace has zero thickens.[br]

Solution:
This problem was solved using the command [b]Surface( , <Angle> )[br][/b][br]Getting this result:[br][br]
This is how the STL looks like:

Axes can also be left out. [br][br]You can try this command in the applet showed before.
Other possibilities when working with 3D objects.
We can so a different pedagogical approach.[br][br]Not only we can visualize but we can touch the mathematical representations of the abstract objects that we are working with. [br][br]Also we can create our own materials that fit to our class and the way we teach.[br][br]See examples below:[br][br][br][br]
Simultaneous equations
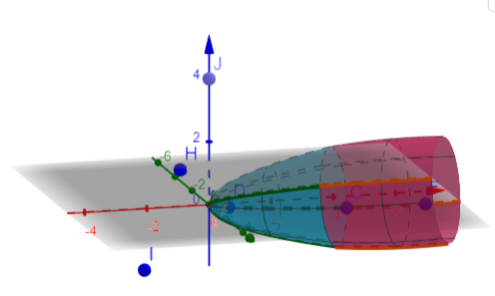
An idea that came to my mind when working with 3D printed objects was to print different simultaneous equations and using the prints to understand the concept of solution. Infinite solutions, impossible system, only one point in the solution.



[br][br] When using this prints, the conversation was really enhanced.[br][br] [br]
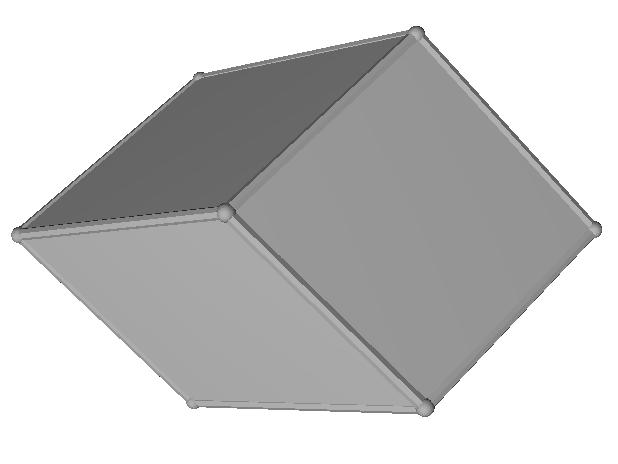
Creating our own materials for the class
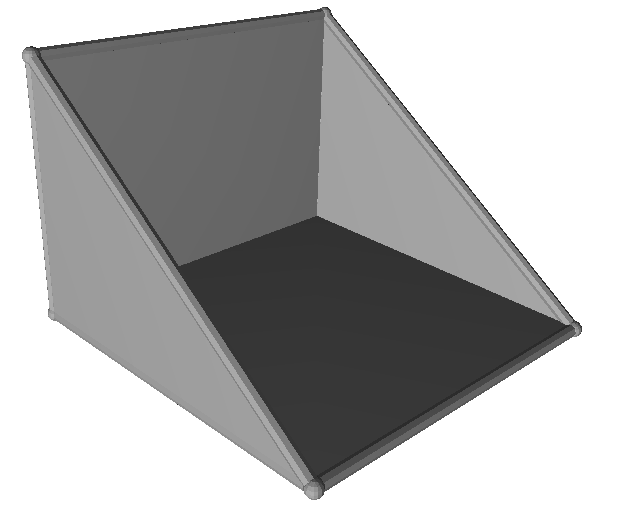
Creating solid that do not come in the "normal" packages, special for our class.[br][br][b]This [/b][b]are STL files cre[/b][b]ated in GeoGebra.[/b]
Functions
We can also print functions to understand the concept of maximums and minimums, derivatives...[br][br][b]This [/b][b]are STL files cre[/b][b]ated in GeoGebra.[/b]
Also we can work with conics and intersections