GeoGebra 3D with AR (iOS): Explorations & Lesson Ideas
This book contains an introduction, lesson ideas, and various means through which math teachers can use GeoGebra 3D Calculator with Augmented Reality (iOS) to create dynamic, student-centered, exploratory learning environments. This volume will continue to grow over time.
Table of Contents
- Getting Started
- GeoGebra 3D with AR (iOS): Quick Setup Instructions
- Quick Demos & Illustrations
- Geometry Demos with Resource Links: GeoGebra 3D with AR (iOS)
- Algebra & Precalculus Demos with Resource Links: GeoGebra 3D with AR (iOS)
- Cross Sectional Specials (Calculus): GeoGebra 3D with AR Demos (iOS)
- AR Modeling Challenges
- Cone and Cylinder AR Modeling Challenge
- Toblerone Candy AR Modeling Challenge
- Cylinder and Hemisphere AR Modeling Challenge
- Solar System Demos
- Season Changes: Sun-Earth Demo
- Algebra & Geometry
- Surface Area: Intuitive Introduction
- Volume: Intuitive Introduction
- Surface of Revolution: 3D Augmented Reality Template
- Diagonal Hint for a Rectangular Prism
- Build Your Own Right Triangular Prism (V2)!
- Unwrapping a Cylinder: REVAMPED!
- Cone Anatomy
- Square Pyramid: Underlying Anatomy
- Sphere as a LOCUS: Quick Exploration and Prompt
- Sphere + Plane = ?
- Cube: Exploration Template
- Tetrahedron: Exploration Template
- Octahedron: Exploration Template
- Dodecahedron: Exploration Template
- Icosahedron: Exploration Template
- Toblerone Warm Up Modeling Question for Algebra, Geometry, AND Calculus!
- Exploring Cross Section and Surface of Revolution Intuitively
- 3D Abe: Silhouette = Surface of REV Cross Section
- Precalculus
- Conic Sections: Introduction
- Parabola: Cause and Effect
- Baby-Step Modeling in 3D GC with AR: Part 1
- Baby Step Modeling in 3D GC with AR: Part 2
- Sphere Investigation
- Varignon 3D Action: REVAMPED!
- How to Create a 3D Surface of Revolution by Rotating ANY 2D Figure about ANY LINE
- Calculus
- Surface of Revolution: 3D Augmented Reality Template
- Disc Method: REVAMPED!
- Disc Action!!!
- Washer Method: REVAMPED!
- Cylindrical Shells: REVAMPED!
- Calculus: Surface of Revolution formed by Rotating Area Between 2 Functions
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VA)
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VB)
- Modifiable Solid: Equilateral Triangle Cross Sections Parallel to yAxis
- Toblerone Warm Up Modeling Question for Algebra, Geometry, AND Calculus!
- Modifiable Solid: Isosceles Triangle (Modifiable) Cross Sections Parallel to yAxis
- Modifiable Solid: Square Cross Sections Parallel to yAxis
- Custom Solid: Changeable Rhombus Cross Section Parallel to yAxis
- Modifiable Solid: Regular Pentagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Hexagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Heptagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Octagonal Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Nonagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Decagon Cross Sections Parallel to yAxis
- Modifiable Solid: Semicircular Cross Sections Parallel to yAxis
- Custom Solid: Elliptical Cross Sections Parallel to yAxis
- Solids with Various Cross Sections: AR Templates
- Arc Length to Surface of Revolution: Calculus
- Partial Derivatives: Graphical Illustrator
- Plotting Points in 3D: AR Template
- Cylindrical Coordinates: Dynamic Illustrator
- Spherical Coordinates: Dynamic Illustrator
- Circular Paraboloid of Revolution: 3D Augmented Reality Template
- Special Hyperboloid of 1 Sheet as a Locus
- Special Hyperboloid of 2 Sheets as a Locus
- Ellipsoid: Quick Exploration Template
- Special Spheroid Action: Locus Illustration
- 3 Tori Morphing
- Surface of Rev with Helical Cross Section
- Miscellaneous
- Shortest Path Between 2 Points on a Sphere
- 3 Golden Rectangles Surprise!
- Dodecahedral Surprise!
- Holiday Fun!
- Seashell Surface
- Dandelin Sphere Action!
- Modifiable Torus
GeoGebra 3D with AR (iOS): Quick Setup Instructions
WHAT TO DO:
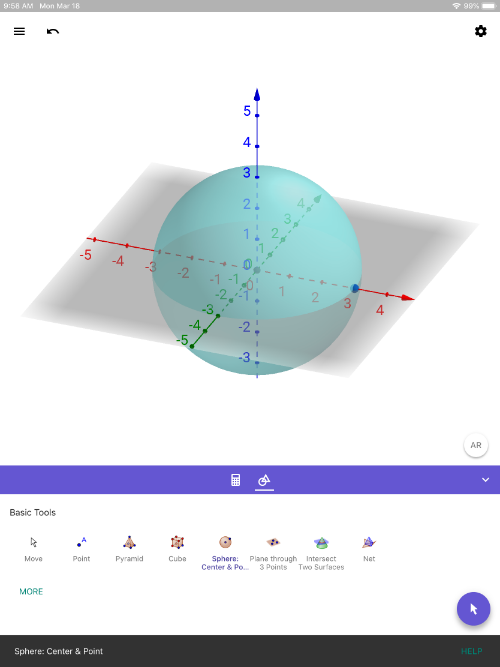
1) Here's the link to [url=https://itunes.apple.com/us/app/geogebra-3d-graphing-calc/id1445871976]GeoGebra 3D Calculator[/url] on AppStore. Install it on your iOS device. [br][br]2) Once it's installed, open the app. Use the app to create any 3D solid. [br] Here, we simply created a sphere by using the SPHERE WITH CENTER THROUGH POINT [icon]https://www.geogebra.org/images/ggb/toolbar/mode_sphere2.png[/icon] tool. [br] (This tool is the 5th one in on the left on the top row in the pic below). [br]
3) Next, press the [b]AR [/b]button (lower right within 3D Graphics pane). You'll see everything disappear and you'll see your environment on the screen. Move your device slowly, making sure to AIM IT AT THE FLOOR. Wait a few seconds. Look for a SQUARE to appear. Once you see it, touch anywhere on the screen to place the object in your environment. [br][br]Use your fingers to reposition the objects. KEY IS TO MOVE SLOWLY. [br][b][color=#1e84cc]Have fun exploring! [br][br][/color][/b]4) Press the 3D button (lower right) to exit AR view.
Quick (Silent) Demo (done on iPad)
Quick (Silent) Demo (done on iPhone)
Geometry Demos with Resource Links: GeoGebra 3D with AR (iOS)
Below is a list of quick screencasts that illustrate how GeoGebra 3D with Augmented Reality (AR) can provide both teachers and students an ACTIVE, HANDS-ON approach to exploring some geometry concepts.[br][br][b]Enjoy! [/b][br][br]All screencasts shown here were recorded on an iPadPro (larger screen) or iPhone10sMax (smaller screen).
EXPLORING SURFACE AREA OF A RECTANGULAR PRISM
Link to GeoGebra resource shown above can be found [b][color=#0000ff][url=https://www.geogebra.org/m/rmfptnzu#material/fmbmkpj7]here[/url][/color][/b].
EXPLORING VOLUME
Link to GeoGebra resource shown above can be found [b][color=#0000ff][url=https://www.geogebra.org/m/rmfptnzu#material/dp6ghmvv]here[/url][/color][/b].
FINDING THE DIAGONAL OF A RECTANGULAR PRISM: BIG HINT
Link to GeoGebra resource shown above can be found [b][color=#0000ff][url=https://www.geogebra.org/m/rmfptnzu#material/NNUNEtR8]here[/url][/color][/b].
MODIFIABLE TRIANGULAR PRISM STUDENTS CAN EXPLORE
Link to the GeoGebra resource shown above can be found [b][color=#0000ff][url=https://www.geogebra.org/m/rmfptnzu#material/j6xVky5C]here[/url][/color][/b].
ANATOMY OF A SQUARE PYRAMID
Link to GeoGebra resource shown above can be found [b][color=#0000ff][url=https://www.geogebra.org/m/rmfptnzu#material/V9cAn76T]here[/url][/color][/b].
Cone and Cylinder AR Modeling Challenge
In the screencast below, both the cylinder and cone have equal radii and equal heights. [br]The height of each is double the radius. [br]Their circular bases are tangent to each other. [br][br]How can we construct this 3d image in GeoGebra 3D Graphing Calculator on your device? [br]Try to do so, and then project what you create in Augmented Reality. [br][br]If you're up for it, you can find such solids or create them from cardstock and put them to the "AR TEST" as shown in the screencast below. [br][br][b][color=#1e84cc]How well do the virtual images place when superimposed on top of the real world objects? [/color][/b]
Quick Demo
Season Changes: Sun-Earth Demo
Even though the [b][color=#bf9000]Sun[/color][/b] and [b]Earth [/b]are not constructed to scale (nor is the distance between the centers of these two masses) , the [b]Earth[/b] (shown here as [b][color=#1e84cc]northern hemisphere[/color][/b] and [b][color=#ff00ff]southern hemisphere[/color][/b]) does have an axis that is tilted approximately 23.5 degrees about its center with respect to the line that is perpendicular to the plane containing its orbit.
1.
For the hemisphere in which you live, what Sun-Earth event does [b][color=#ff7700]point A[/color][/b] represent? [br]What does [b][color=#ff7700]point B[/color][/b] represent? What about [color=#ff7700][b]point C[/b][/color]? What about [b][color=#ff7700]point D[/color][/b]? [br][br]Give reasons for your responses.
TO EXPLORE IN AUGMENTED REALITY:
1) Open up GeoGebra 3D app on your device. [br][br]2) Go to the MENU (horizontal bars) in the upper left corner. Select OPEN. [br] In the Search GeoGebra Resources input box, type [b]jdkh6cz8[/b][br] (Note this is the resource ID = last 8 digits of the URL for this resource.)[br][br]3) The buttons will not appear in the 3D app. However, the sliders SPIN and SPEED will. [br] (Simply alter these and nothing else.)
Surface Area: Intuitive Introduction
TEACHERS:
For an introductory class activity related to this, [url=https://www.geogebra.org/m/mgwejudc]click here[/url].
Conic Sections: Introduction
Explore with this app for a bit. Then use it to help answer the thinking questions that follow.
1.
[color=#bf9000][b]Note the equation of the plane is z = some constant. [/b][/color][color=#bf9000][b]Change the equation of this yellow plane to z = 2. [br]Then change it to z = 1. [br]Then change it to z = 4. [/b] [/color][br][br]How would you describe the intersection of this [b][color=#bf9000]plane[/color] [/b]and [color=#1e84cc][b]double-napped cone[/b][/color]?
2.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
3.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=0.5x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
4.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=4x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
Shortest Path Between 2 Points on a Sphere
In the context of a [color=#38761d][b]SPHERE[/b][/color], [br][br]A [color=#1e84cc][b]GREAT CIRCLE[/b][/color] is defined to be a [b][color=#1e84cc]CIRCLE[/color][/b] that lies on the [b][color=#38761d]SURFACE OF THE SPHERE[/color][/b] and [b]LIES ON A PLANE that PASSES THROUGH THE CIRCLE's CENTER.[/b] In essence, the center of a [b][color=#1e84cc]GREAT CIRCLE[/color][/b] and the center of the [b][color=#38761d]sphere[/color][/b] are the same. [br][br]Consequently, a [b][color=#1e84cc]GREAT CIRCLE[/color][/b] also the largest possible circle one can draw on a [b][color=#38761d]sphere[/color][/b]. [br][br]In the applet below, the [b][color=#ff00ff]pink arc[/color][/b] and [b][color=#1e84cc]blue arc[/color][/b] make up a [b][color=#1e84cc]GREAT CIRCLE. [/color][/b] [br][br][b][color=#1e84cc]To explore this resource in Augmented Reality, see the directions below the applet. [/color][/b]
1.
Note that the [b]black arc[/b] and [color=#bf9000][b]yellow arc[/b][/color] (put together) DO NOT make a great circle. Why is this?
See below this applet for directions.
[b]Directions: [/b] [br][br]Move the [b]2 WHITE POINTS[/b] anywhere you'd like on the [b][color=#38761d]sphere[/color][/b]. The [b][color=#ff00ff]PINK ARC[/color][/b] is part of a [b][color=#1e84cc]GREAT CIRCLE[/color][/b] of this [color=#38761d][b]SPHERE[/b][/color]. You can move the [b][color=#bf9000]YELLOW POINT[/color][/b] anywhere you'd like as well. [br][br]Again, note that the [b][color=#bf9000]YELLOW ARC[/color][/b] is [b][color=#bf9000]NOT PART[/color][/b] of a great circle. [br][br]Slide the slider slowly and carefully observe what happens.
2.
How would you describe the SHORTEST DISTANCE between 2 POINTS along a [b][color=#38761d]SPHERE[/color][/b]? Explain.
TO EXPLORE IN AUGMENTED REALITY:
1) Open GeoGebra 3D app on your device. [br][br]2) Press the 3 horizontal bars (upper left corner). Select OPEN. [br][br]3) In the SEARCH TAB that appears, type [b]Gh58sVPx[/b][br] Note this string of characters can be found in the URL here. [br] Be sure to either copy & paste this code or type it just the way you see it here. [br][br]4) The slider named[b] j[/b] controls the entire animation. [br] Slider [b]k_1[/b] adjusts the opacity (shading) of the green sphere. [br] Slider [b]a[/b] adjusts the radius of the sphere.