Theorems on Inscribed Angles

Part 1: Definition of an Inscribed Angle:

[u]An inscribed angle[/u] is an angle made form points sitting on a circle's circumference. [br]

Looking at the circle with center C above, notice that it has points B, A, and D that lies on its circumference. [br]So Circle C has an inscribed angle, [math]\angle[/math]BAD.

Move Point A around the circle.

Observe the measure of [math]\angle[/math]BAD as you move Point A between points B and D. What do you notice about the measure of the angle?

Move Points B and D around the circle.

Remember that the inscribed angle is [math]\angle[/math]BAD. [br]When moving Points B and D, what changed about the inscribed angle? [br]

Based on your answer above, what decides the measure of an inscribed angle?

Part 2: Inscribed Angles Theorems

In this section, we will be learning about two inscribed angle theorems -[b] the central angle theorem[/b] and [b]the angles subtended by the same arc theorem[/b].

[b][u][color=#bf9000]The Central Angle Theorem[/color][/u][/b]

In the above circle with Center A, the measure of [math]\angle[/math]BAC and [math]\angle[/math]BDC are given. [br]Is there anything you notice about these two angles? What is their relationship?

Move around Point D.[br]Do you see that the measure of its angle never changes?

Definition of The Central Angle Theorem:

In the circle provided above, we see that there is center A. [br]This [b]center along with two points that lie on the circle[/b][u],[/u] forms[math]\angle[/math][b][color=#ff0000]BAC[/color].[/b] This is the central angle. [br]The same [b]two points that lie on the circle [color=#0000ff](Points B and C)[/color], along with another point that lies on the circle [color=#0000ff](Point D)[/color][/b], creates an inscribed angle that is equal to half of the central angle. That is, [math]\angle[/math][color=#ff0000][b]BDC. [/b][/color]

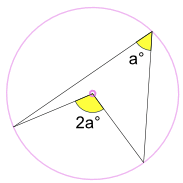
[size=100]In this photo, we have a central angle and an inscribed angle. These angles have the same arc. We see that the central angle is equal to two times the inscribed angle. [/size]

[u][b][color=#bf9000]The Angles Subtended By the Same Arc Theorem[/color][/b][/u]

In the above circle with Center A, the measure of [math]\angle[/math]BEC and [math]\angle[/math]BDC are given. [br]Is there anything you notice about these two angles?

Move around points D and E. [br]Notice that the measure of their angles never change. [br]This is because they are inscribed angles; the measure of [math]\angle[/math]BEC and [math]\angle[/math]BDC will be the same if points D and E are outside of [color=#93c47d]green arc BC. [/color]

Definition of Angles Subtended by Same Arc:

No matter where it is on the same arc between end points, the [color=#cc0000]angle a [/color]is always the same.

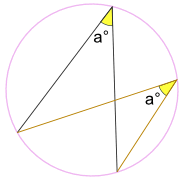
[size=150][size=100]In this photo, we have two angles with the same measure of a°. These two angles are constructed by same two points that lie on the circle. Any angle constructed that share same endpoints will have the same measure of a°.[/size][/size]

Question:

In the above circle, how many degrees are [math]\angle[/math]G and [math]\angle[/math]I?

Learning Check

Select all the sentences that are true about Inscribed Angles, The Central Angle Theorem, and The Angles Subtended By The Same Arc Theorem.

Inscribed Angles are made up of three points that lie on a circle. For an angle to be subtended by the same arc, they have to have the same endpoints, the two points that lie on the circle. Angles that are subtended by the same arc will have different measures. Inscribed Angles' measures are equal to half of the circle's central angle. Inscribed Angles will have the same measure as its circle's central angle. The measure of a Central Angle depends on the two points that lie on the circle. Central angles are made up of two points that lie on a circle, and the center point of a circle. Central Angles are made up of three points that lie on a circle. If you have the measure of one angle that subtends an arc, you will have the measure of any other angle that subtends that same arc.