Parametervariation bei der e-Funktion
Selbstlerneinheit mit Aufgaben zur Sicherung des Wissens zur Variation der Paramater bei der natürlichen Exponentialfunktion [math]f(x)=a\cdot e^{k\doct x -d} + c[/math] Bearbeiten Sie alle 4 Kapitel!
Table of Contents
- Addition eines konstanten Werts zum Funktionsterm
- Parametervariation: g(x)=exp(x)+c
- Subtraktion eines konstanten Werts im Exponenten
- Parametervariation: g(x)= e^(x-d)
- Variation des Anfangswerts
- Parametervariation: g(x)=a*e^x
- Variation der Wachstumskonstanten
- Parametervariation: g(x)=e^(k*x)
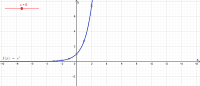
Parametervariation: g(x)=exp(x)+c
Einführung
Gegeben ist der Graph der Funktion f mit . [br]Zur Funktionsgleichung wird nun auf beiden Seiten ein konstanter Wert ( hier "c" genannt) addiert. [br]Es entsteht der Graph der neuen Funktion g mit . [br]Bewegen Sie den Schieberegler, um sich darüber einen Eindruck zu verschaffen.
Arbeitsauftrag 1
Bearbeiten Sie die Aufgabe auf Niveau I oder Niveau II[br][br]Niveau I: [br]Beschreiben Sie, wie sich der Wert des Parameters c auf [br]den Graphen der Funktion g auswirkt ([i]Erwartung: [u]Mindestens[/u] 2-3 [br]vollständige Sätze unter [b]Verwendung von Fachsprache[/b][/i]).[br][br]Niveau II: [br]Verfassen Sie einen [u][b]erklärenden[/b][/u] Text, wie sich der Wert des Parameters c auf [br]den Graphen der Funktion g auswirkt ([i]Erwartung: [u]Mindestens[/u] 3-4 [br]vollständige Sätze unter [b]Verwendung von Fachsprache[/b][/i]).
Arbeitsauftrag 2
Gegeben sind die beiden Funktionen und .[br]Beide Graphen werden nun um 3 Einheiten nach unten verschoben.[br]Geben Sie für die beiden neuen Graphen jeweils die zugehörige Funktionsgleichung an.
Parametervariation: g(x)= e^(x-d)
Einführung
Wir betrachten nun bei der natürlichen [b]Exponentialfunktion[/b], was passiert, wenn der Parameter nicht [u]nach Berechnung[/u] des ursprünglichen Funktionswerts addiert, sondern direkt innerhalb der Funktionsgleichung zur Variablen "x" addiert bzw. subtrahiert, [u][b]bevor man den Funktionswert berechnet:[br][math]g\left(x\right)=e^{x-d}[/math][br][/b][/u][br]
Verändere den Wert des Parameters d mit dem Schieberegler.
Aufgabe 1
Vervollständigen Sie die beiden Sätze und geben Sie für jeden Satz auch eine oder zwei Funktionsgleichungen als Beispiele an.[br]1.) Ist der Wert von d positiv, dann....[br]2.) Ist der Wert von d negativ, dann...
Aufgabe 3
Der Graph einer Exponentialfunktion mit [math]f(x)=e^x[/math] wird verschoben. [br]Geben Sie die Funktionsgleichung der neuen Funktion g an.[br]a.) Verschiebung um drei Einheiten nach rechts.[br]b.) Verschiebung um eine halbe Einheit nach links.[br]c.) Verschiebung um eine 3/4 Einheit nach rechts und um 2 Einheiten nach unten.
Parametervariation: g(x)=a*e^x
Einführung
In dieser Lektion wird die gesamte Funktion mit dem Parameter[b] multipliziert[/b] und die Auswirkungen dessen untersucht.
Aufgabe 1
Was verändert sich, wenn man eine Funktionsgleichung mit einem konstanten Faktor multipliziert?[br][b]Beschreiben Sie[/b] Ihre Beobachtungen und [b]klassifizieren Sie[/b] (sortieren in Gruppen/Bereiche) bezüglich Werten des Parameters a.
Aufgabe 2 - Bearbeiten Sie Niveau I oder II
Betrachte die gegebenen Punkte E, A und C im Applet.[br]Wie verändern sich jeweils die beiden [b]Koordinaten[/b] der Punkte, wenn man den Wert des Parameters variiert?[br]Niveau I:[br][b]Beschreiben Sie [/b]Ihre Beobachtungen.[br][br]Niveau II:[br][b]Berechnen[/b] [b]Sie[/b] die neuen Koordinaten der Punkte E', A', C',...[br][list][*] wenn a = 2,[/*][*]wenn a = 0,5,[/*][*]wenn a = -3 beträgt.[/*][/list][b]Erkläre[/b]n Sie Ihren Rechenweg: Warum funktioniert das so?
Betrache die folgenden Graphen.
Aufgabe 3
[b]Geben Sie[/b] die Funktionsgleichungen der zu den Graphen gehörenden Exponentialfunktionen [b]an[/b].[br][b]Erläutern Sie[/b] dazu die besondere Bedeutung des Schnittpunkts mit der y- Achse.