Copy of TEOREMA PYTHAGORAS

Sejarah Singkat Teorema Pythagoras

[justify][b]Pythagoras (582 SM - 469 SM)[/b] lahir di pulau Samos, Ionia, Yunani Selatan. Salah satu peninggalan Pythagoras yang paling terkenal hingga saat ini adalah teorema Pythagoras. Teorema Pythagoras menyatakan bahwa [i]"kuadrat sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat dari sisi-sisi yang lain"[/i]. Uniknya, ternyata rumus ini 1.000 tahun sebelum masa Pythagoras. Orang-orang Yunani sudah mengenal perhitungan "ajaib" ini. Walaupun faktanya isi teorema ini telah banyak diketahui sebelum lahirnya Pythagoras, namun teorema ini dianggap sebagai temuan Pythagoras, karena ia yang pertama membuktikan pengamatan ini secara matematis. Pythagoras menggunakan metode aljabar untuk membuktikan teorema ini.[/justify]

Apa Itu Teorema Pythagoras?

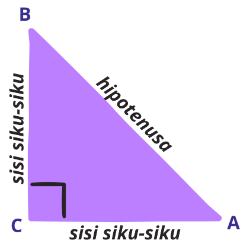
[justify]Teorema Pythagoras menyatakan bahwa kuadrat dari sisi miring (hipotenusa) sama dengan jumlah kuadrat sisi lainnya pada segitiga siku-siku.[/justify]Ada beberapa unsur segitiga, perhatikan segitiga ABC atau [math]\bigtriangleup ABC[/math] di bawah ini:[br]

[justify]Sisi di depan sudut siku-siku [math]\angle C[/math] merupakan sisi terpanjang dan dinamakan hipotenusa. Sisi CA dan sisi AB, sisi lain yang membentuk sudut siku-siku disebut dengan sisi siku-siku.[br]Setiap segitiga siku-siku berlaku luas persegi pada hipotenusa sama dengan jumlah luas persegi pada sisi yang lain (sisi siku-siku).[/justify]

Pembuktian Teorema Pythagoras

[justify]Pembuktian Teorema Pythagoras berkaitan erat dengan luas persegi dan segitiga. Untuk memeriksa kebenarannya, lakukan kegiatan di bawah ini:[/justify]

Rumus Teorema Pythagoras

[justify]Pembuktian teorema Pythagoras dilakukan dengan cara mempelajari luas.[br]Namun demikian teorema ini dapat digunakan untuk menghitung panjang suatu sisi, sehingga dari teorema Pythagoras dapat diturunkan hal berikut ini.[br]Bila [math]\bigtriangleup ABC[/math] siku-siku di titik C, maka berlaku:[/justify]

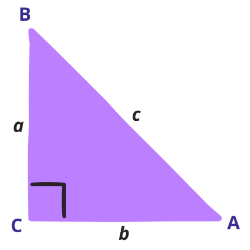
[math]BA^2=CB^2+CA^2[/math][br]atau[br][math]c^2=a^2+b^2[/math][br]atau[br][math]a^2=c^2-b^2[/math][br]atau[br][math]b^2=c^2-a^2[/math]

Triple Pythagoras

[justify]Sesuai dengan namanya, triple Pythagoras adalah [i]tiga bilangan bulat[/i] yang merupakan sisi-sisi bangun segitiga siku-siku yang telah memenuhi aturan dari teorema pythagoras. Dengan mengingat triple Pythagoras kita dapat dengan mudah menentukan panjang salah satu sisi bila diketahui dua panjang sisi lainnya.[br][br]Apa saja angka-angka triple Pythagoras yang sudah kalian temukan? Diskusikan dengan temanmu menurut hasil kegiatan sebelumnya.[/justify]

[b][color=#9900ff][size=150]LATIHAN SOAL[/size][/color][/b]

Soal 1

Pada sebuah segitiga PQR diketahui sisi-sisinya p, q, dan r. Dari pernyataan berikut yang benar adalah...

Jika [math]p^2=q^2+r^2,[/math] maka [math]\angle P=90^\circ[/math] Jika [math]q^2=p^2+r^2,[/math] maka [math]\angle P=90^\circ[/math] Jika [math]r^2=q^2-p^2,[/math] maka [math]\angle R=90^\circ[/math] Jika [math]r^2=p^2-q^2,[/math] maka [math]\angle Q=90^\circ[/math]

Soal 2

Sebuah segitiga ABC siku-siku di B, di mana [math]AB=8cm,[/math] [math]AC=17cm[/math]. Panjang BC adalah...

[math]15cm[/math] [math]25cm[/math] [math]9cm[/math] [math]68cm[/math]

Soal 3

Panjang hipotenusa sebuah segitiga siku-siku sama kaki [math]16cm[/math] dan panjang kaki-kakinya [math]x[/math] [math]cm[/math]. Nilai [math]x[/math] adalah ... cm

[math]4\surd2[/math] [math]4\surd3[/math] [math]8\surd2[/math] [math]8\surd3[/math]

Soal 4

Perhatikan segitiga [math]PQR[/math] pada gambar di bawah!

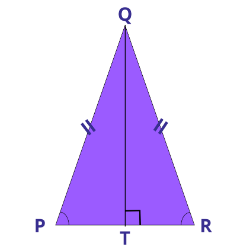
Panjang [math]PQ=QR=13cm[/math] dan [math]QT=5cm[/math]. Panjang [math]PR=...[/math]

8 cm 12 cm 24 cm 6 cm

Soal 5

Perhatikan gambar berikut ini!

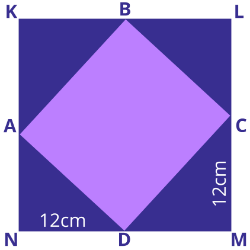
Panjang sisi KLMN pada gambar adalah 17 cm. Keliling ABCD adalah...