de 3D grafische rekenmachine
Welkom bij de [url=https://www.geogebra.org/3d]GeoGebra 3D rekenmachine[/url]! Leer hoe je lichamen kunt tekenen, rotaties en doorsnedes kunt tonen in 3D, objecten verkennen met Verhoogde realiteit en veel meer met deze initiatiehandleiding.
Table of Contents
- Eerste stappen
- vergelijking van de GeoGebra apps
- Inleiding
- Verken de app
- Algebravenster
- Knoppenvenster
- 3D tekenvenster
- Verhoogde realiteit (VR)
- Basis
- Cilinder en kubus
- Modellen in Verhoogde realiteit
- Rotaties
- doorsnedes van een kegel
- Cirkels in 3D
- Geavanceerd
- Boldriehoeken
- kwadrieken
- Veelvlakken met spiegelingen
- YouTube initiatiehandleidingen
- Ruimtemeetkunde in SO
- Punten, lijnstukken, rechten en veelhoeken in de ruimte
- Ruimtelichamen, vlakken en onderlinge ligging
- omwentelingslichamen
- Analytische ruimtemeetkunde
- onderlinge ligging in Notitieblok
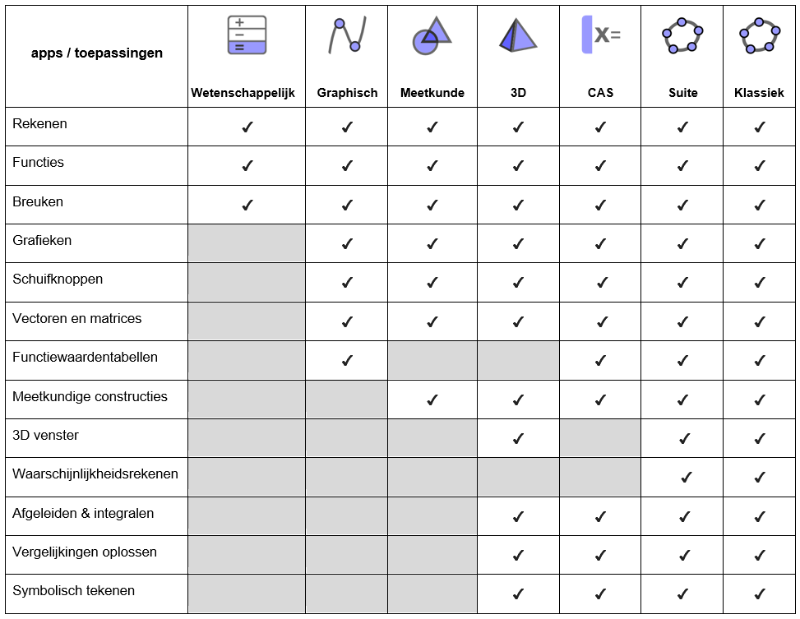
vergelijking van de GeoGebra apps
Met onze GeoGebra wiskunde apps kan je functies, meetkunde, algebra, statistiek en 3D verkennen en leren op een nieuwe en educatieve manier.[br][list][*][url=https://www.geogebra.org/scientific]Wetenschappelijk rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafisch rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/geometry]Meetkunde[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rekenmachine suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/3d]3D rekenmachine[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Klassiek[/url][br][/*][/list]De juiste app voor jou is die app die tegemoet komt aan je noden en, voor gebruik in toetsen of examens, beantwoordt aan de voorschriften van je school of regio. In onderstaande tabel vind je een overzicht van de ingebouwde toepassingen in de verschillende apps.
GeoGebra in toetsen en examens
We geloven dat het goede zaak is dat leerlingen exact dezelfde GeoGebra app kunnen gebruiken in de klas, thuis en tijdens testen en examens. Op deze manier kunnen ze meer oefening opdoen met de app en ze op de beste manier gebruiken in alle situaties. Daarom hebben we onze [url=https://www.geogebra.org/m/y3aufmy8]GeoGebra Examenmodus[/url] gecreëerd en ingebouwd in al onze apps. De examenmodus vergrendelt mobiele toestellen zodat leerlingen niet kunnen communiceren of andere apps gebruiken tijdens een test. Deze benadering werd al uitgetest en goedgekeurd door meerdere ministeries van onderwijs in meerdere regio's. Lees meer over het gebruik van de examenmodus in de initiatiehandleiding [url=https://www.geogebra.org/m/scntsjc9]GeoGebra examenmodus[/url].[br][br]
Cilinder en kubus
Opgave
Construeer een cilinder en een kubus.[br]Verken in volgend applet hoe je een cilinder en een kubus creëert met de [i][url=https://www.geogebra.org/calculator]GeoGebra Rekenmachine Suite[/url][/i]. Volg daarna de constructies en probeer het zelf.
Verken de constructie...
Wanneer je de [i]GeoGebra 3D rekenmachine [/i]gebruikt op een smartphone die VR ondersteunt, kan je schakelen naar [i]VR modus[/i] en de wiskundige objecten die je creëerde op een willekeurig plat oppervlak rondom je plaatsen (b.v. tafel, vloer, ...) en errond wandelen. Verken je constructies vanuit een nieuw perspectief!
Instructies
[table][tr][td]1. [/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Open de [i]instellingen[/i] en selecteer [i]Toon rooster[/i]. [/td][/tr][tr][td]2.[/td][td][/td][td]Typ in het invoerveld van het [i]Algebra [/i][i]venster [/i]het commando [math]Cilinder((2,-3,-1),(2,2,2),2)[/math] om een cilinder te creëren door twee punten met een straal van 2 en [i]Enter[/i]. [/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Verken verschillende [i]Projectiemethodes[/i] in de [i]instellingen[/i]. [/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Schakel naar het knoppenvenster, selecteer de knop [i]Punt [/i]tool[i] [/i]en creëer twee nieuwe punten. [/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_cube.png[/icon][/td][td]Selecteer de knop [i]Kubus [/i]en construeer een kubus door de gecreëerde punten te selecteren.[/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Selecteer de knop [i]Verplaatsen [/i]en verken je constructies. [br][/td][/tr][/table]
Doe het zelf...
Boldriehoeken
Opgave
Creëer driehoeken op een cirkel[br][br]Bekijk onderstaande constructie en verken hoe je boldriehoeken creëert met de [i][url=https://www.geogebra.org/3d]GeoGebra 3D rekenmachine[/url][/i]. Volg daarna de instructies van het stappenplan en probeer het zelf.
Instructies
[table][tr][td]1.[/td][td][/td][td]Typ in het [i]invoerveld [/i]van het [i]algebra [/i][i]venster[/i] [math]A=(0,0,0)[/math] en het commando [math]Bol(A,1)[/math].[/td][/tr][tr][td]2.[/td][td][/td][td]Selecteer de bol in het [i]3D tekenvenster[/i] en kies [img]https://wiki.geogebra.org/uploads/thumb/d/d5/Color_button.svg/16px-Color_button.svg.png[/img] [i]Kleur[/i] in de [i]opmaakwerkbalk [/i]om de kleur van de bol te wijzigen.[br][/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Open de [i]Instellingen[/i] and vink [i]Toon assen[/i] en [i]Toon grondvlak [/i]uit.[/td][/tr][tr][td]4.[/td][td][/td][td]Schkel naar het knoppenvenster[i]. [/i][/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Selecteer de knop [i]Punt [/i]en creëer de drie punten [i]B[/i], [i]C [/i]en [i]D [/i]op de bol. [/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_circlearc3.png[/icon][/td][td]Selecteer de knop [i]Cirkelboog, [/i]selecteer eerst [i]A[/i] als middelpunt en daarna [i]B[/i] en [i]C[/i]. Herhaal dit twee keer met de andere punten om een boldriehoek te creëren (selecteer steeds eerst punt [i]A[/i]).[br][/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Gebruik de knop [i]Verplaatsen [/i]om de punten op de bol te verslepen en verken je constructie.[br][/td][/tr][/table]
Probeer het zelf...
Verhoogde realiteit
Wanneer je de [i]GeoGebra 3D rekenmachine[/i] gebruikt op een smartphone die VR ondersteunt, kan je schakelen naar VR modus en de wiskundige objecten die je creëerde op een willekeurig plat oppervlak rondom je plaatsen (b.v. tafel, vloer, ...) en errond wandelen. [br]Verken je constructies vanuit een nieuw perspectief!
Punten, lijnstukken, rechten en veelhoeken in de ruimte
Punten lijnstukken en veelhoeken
Selecteer de knop [icon]/images/ggb/toolbar/mode_point.png[/icon] [i]Punt [/i]en klik op het [i]Oxy [/i]grondvlak in het [i]3D tekenvenster[/i]. [br][b]Tip:[/b] Je kunt schakelen tussen horizontaal of verticaal bewegen van een punt door het punt te selecteren. Bij het selecteren verschijnen pijlen naast het punt die de bewegingsrichting aanduiden.[br]Opmerking: Met de knop Punt kan je enkel punten creëren op een bestaand object (het Oxy grondvlak, een eerder gecreëerde rechte, veelhoek of ruimtelichaam). Je kunt ook een punt creëren door als invoer 3D-coördinaten in te geven: De invoer (1, 2, 1) creëert een punt met gegeven x-, y- en z-coördinaat.[br][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_segment.png[/icon] [i]Lijnstuk [/i]en klik tweemaal in het [i]Oxy [/i]grondvlak of op bestaande punten.[br]Je creëert ook een lijnstuk met het commando [b]Lijnstuk( )[/b].[br][list][*][b]Lijnstuk(A, B)[/b] creëert een lijnstuk tussen twee gegeven punten A en B.[/*][*][b]Lijnstuk((1,0,2), (0, 1, 3))[/b] creëert een lijnstuk tussen twee punten met gegeven coördinaten.[/*][/list][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_polygon.png[/icon] Veelhoek, klik op de hoekpunten en sluit de veelhoek door nogmaals het eerste hoekpunt aan te klikken. Analoog als in 2D kan je veelhoeken ook bepalen als bv. [b]Veelhoek(A, B, C, D)[/b].
Rechten
[list][*][i]Twee punten:[/i][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_join.png[/icon] Rechte en klik op twee punten, of definieer een rechte met het commando Rechte(A,B). [/*][*][i]Punt en evenwijdige rechte:[/i][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_parallel.png[/icon] Evenwijdige Rechte, klik op een bestaande rechte en een bestaand punt en creëer de rechte door het punt evenwijdig met de eerste rechte. De volgorde van aanklikken maakt niet uit. Je creëert ook een rechte door het punt A evenwijdig met de rechte a als [b]Rechte(A, a)[/b].[/*][*][i]Punt en richtingsvector:[/i][br]Het commando [b]Rechte(Punt, Richtingsvector)[/b] creëert een rechte door een gegeven punt met gegeven richtingsvector. [br][u]Let op[/u]: Vul voor de richtingsvector geen richtingsgetallen in. GeoGebra interpreteert deze coördinaten als de coördinaten van een gegeven punt. Definieer eerst een vector als bv. u=(1, -1, -1). Door een kleine letter te gebruiken weet GeoGebra dat u een vector is. [br][b]Rechte(A, u)[/b] of [b]Rechte((1, 2, 1), u)[/b] creëert een rechte door het gegeven punt met gegeven richtingsvector.[br][br][/*][/list]
Experimenteer in het 3D venster met punten, lijnstukken, veelhoeken en rechten
Instellingen
Klik op de knop Instellingen in de rechterbovenhoek van het 3D venster en ontdek de mogelijke instellingen.[br][list][*]De assen, het Oxy grondvlak en een raster in dit grondvlak kunnen naar keuze getoond of verborgen worden. Je kunt ook kiezen tussen enkele projectiemethodes.[/*][*]Zo kan je net als in het 2D tekenvenster de assen een label of vaste verdeling geven.[br]Ook kan je desgewenst de 3 assen zwart kleuren ipv rood, groen en blauw.[/*][*]Met clipping bepaal je de grootte van een kubus die vastlegt tot waar objecten getoond worden. Zo lopen rechten niet langer door tot de rand van het 3D venster. [/*][*]De optie belichting geeft ruimtelichamen een extra 3D-effect.[/*][/list]