Rozšířená realita - AR - Augmented reality
U mnohých úloh této knihy lze využít tzv. AR - rozšířenou realitu.[br][br]Jak postupovat a co je třeba se dozvíte buď ve videu, anebo v instrukcích pod videem.
1) Stažení aplikace
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAL8AAAC5CAYAAAB5s+4bAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAF5iSURBVHhe7f2He5zV8caN//6U97p+7zcBbEvb1NwbNs0YG4OrtL2rWO7GNjbuuBfVVXMBAiQEQkgn1EAIpEDoLfRucO+W7/e+z7OPtJLWxjaW6w7X8Oyu1qvV7mfmzJwzZ87/DznJyVUqlwX8J0+exPHjx3H06FEcPnwYhw4dwoEDB7B//37s27cPe/fuxZ49e3J6kVSfv74HfR/6XvT96Hs6duwY2tvb09/ipSeXFPz6oAT4wYMHzQe6e/du7Nq1q0N/+OEH85j9gXf/0HN6cTTTCUn1/eh70vf1/fffm6se0/P03eo7PnHihHFqF1MuOvzyDjbs+pAEuT4ofajyIEeOHDFeX4ZxsT+snJyd6PvS96bvWN+jvk8ZgL5f24HpvkYJGcOFlosCvz4QwW17BH0ItkfIAX51iBiQQYgDff/2iK7HLhQDFxR+eQANj4Jef7D+UH0IOcmJPL9GABmA+JAz1Ijfm3JB4JdHt8MaDXMXY4jLyeUjcpIXgpdehV9e3f4jFO/lvHxOzkbk+TUC2CPB+Q6Heg1+wZ7z9Dk5H6KRwA6HdPt8yXmHX9aq5EWqcCcnOTlfopzAdqjnYxQ4r/ArgdWbUwafm7XJSW+IoghNmmgk+KkRxXmDXzFZztvn5EKJRgEtoMnhnqucF/jtedpcQpuTCylytDIA5ZfnIj8JfoU2Al/DUC7MycnFEIU+9mzQ2cpPgl/gK77PSU4upijikAGc7QhwzvDbSUdOcnIpiEYA1YWdTQ5wTvDLwhRr5WL8nFxKIvC/++67M14LOGv49cIaYnq77iInOTkXsdcCzsQxnxX8Glp+6vRSTnLS26LkV/noj8lZwW/P7OQkJ5e6aOr9xxLgM4bfXr3NTWmemWj4fe+998xSfE4uvCgsF6+nWwU+I/gFvF4oF+6cufz73//GggUL8OSTT6YfycmFFjme081InhH8epEziaFyYsk333yDRYsWYfz48bjnnnvw6aefpn+SkwspctqnK7n5UfjPZPjISadoluGRRx7B9ddfj7KyMsRiMdTX13fkSrmw8cKKwJf3z/a5/yj88vrnsnR8tcr//vc/hMNh9O/fH8FgENFo1Ojvfve781qLnpMzFzmebCH7aeHPef2zEyW5qVQKRUVFGDJkCAKBgPH8fr8fM2fONHmALbkR4MKJwM8W+58W/jOdL72aRRDbIP/tb3/D2LFj4XQ6cdNNN5kRQBoKhUwItHz5cnz22Wfmufa/y/z3OekdsWt/usf+p4RfX4iShdxQfXqxwf32228xb948XHfddXC73cYIEokE4vG4gV/eXwbQ1NTUUQyoLyUH/4WRbJM2p4RfQ3iucO30onBQAEsffvhhFBcXo2/fvigoKMBtt92G8vJyJJNJ4/0V/3u9XhP/a/rTDiVz8F8Y0eet6oTMEP6U8Av8XKJ7erGh/eh/H8Hn86FPnz4m5CkpKcHkyZNRUVFhvH8kEjEq8JUHaIR48803zb+V5OC/MKJIJpPprPDLOgR/ppXkJLsoLNywYQM8Ho8B3+VyGfinTJmSFX6NAgp/1q1bZ9YDJJpY0OiRk94VlTvIAGzJCr89N5qTU4vtrZ999lncfPPNBv7CwkJjAJrmnDp1qgl7MuG3Vd5fOcBDDz3UkYTlvH/vi5yMav5tR5MVfg0NuZqU04s+wC+++ALV1dXIy8sz05uK9eX5hw8fbjy84n0lvJrulNrw62eK/zUyaIYoB/6FEX3O8vz2nH8P+PUELQoo4c1JT8kEdefOnSbEUazvcDi6wC/I7dmebPDrqjxB5Q8ffPBB+hVz0tsip2479h7wy6PJOnLx/ulFCevEiRON18/PzzdXhT6a5hw5cqSBOxP87vAr/tfPdb+hocHMROSk90VO3Y77e8CvuCgzKchJT1HitGLFCuPlpTb0dtw/bty4LtDbKuBtA8iEX+HP448/nquavQAivpXPysn3gF+Wkduwcnp55plnTOGawh0B3x3+22+/vQvomQZgP5b5uBbB5syZgxdffDH9G3LSW6KwVYtdMoIe8Gv1MdeO5NSi8ESzOIrxFe50h1+J74QJE84Kfj1XodCqVatMYVxOelcEv2bZesCvH5xt/5OrSR544AEDuj2nr9tS3dZjAwYMMPP4SnYzoT+dKvyRygCam5tzI28viz2h0wP+3I6tU8uHH35oanZUwmDH+5nwayQYNGiQmcM/G/jtUUK3q6qq8Ic//MEMy5LcNOj5F0U2PeDXB61hPVfM1lM0TC5btgw///nPO7x+NvgHDxoMf+D08NuzQII+MzxSOKUaIMX/dvmDvpOcAZxfUWSjtawu8Gt6M1e/31Vs8J5++mlTuKYk1wY/E37F+y63CyNHjDRg2wtc0kTMmu+Pxy349TNdbehttQ1B8/8qf9B3IdEokPtOzp8ostFcfxf47YZUuTqTruHGl19+aWZk/u///q+L1+8Ov1R1/Ab49AKXBX8Sibg9EghwLXJZC12K8+1FL1tLS0sxbdo03HfffQZ6vReNPLnv5fyIONd0Zxf4ZRE5+C3RZyDodG1tbUW/fv0s754Bfib8MgpdlRMIYBv8TPhD4SimV8/DortXM8SZjXAkRvBDafipURlCxIQ+MgD923/+85/m/ei9ZBpkTs5d7LWsHvDrwdyHbMEvefvttzFmzBgT7mgOXwZgA5+pgl9hkUqZM71+J/xxBEIVmDG7EbUN/8XcBb/ENG8MXu80A3wkGjTwRyLlVCsk0qyR4v/M8ofcd/PTRaNpD/jtpd/cB2yJPg/V3lxzzTVdvHw2Ffyq5pTHzoz3bfgV74cjszB77qOoTe3Fmk0fIlmxBoFgmCOCwKdGEoiEq2kMCTMaKNRSCcXGjRs76lHsESD3HZ27yLEpwukCvzLgXClzpzz91NOmSE0hTzbgM9WGX7F6Vvg1uxOfiyXL/oz65n1o2nYUa1a/gMqKZQhEAghFGf5EphP6GR3wS1X+rFHg0Ucf7ZiFy4H/00WlzTn4MyTTo2qjucC99tprzWpuNuAzVfDLUOyODR0aTSARreA1hnhyPtZueB6NbQfQ3Aq01e/FirsfRzQ6m3G+tjsK/GrCbtX8SDUDpNecPn06Xn755Y4EOCc/TXrAr8n/qx1+iWZWVGmp+F5lyqeK8zNV8KuaU95awNrwxxnKJCMW/Iny+Vi36UWkth1AqgnY2Qg0b/4Ei+bdh1BwHoLhcoSjSURNzN85/6+cwO/3mWK6zO4POTl3UR//HPxZ5D//+Y+ZtVG4oyRWBpAN+EzV6CD4Fad3gZ+ePynPT2+eSC7Euo3/QKrtEBoJf1sdsK3mCDbd+wYqyjfDGyxn+EPgY1rt1WtY8GsmKBQOmBFg+/btufKH8yA5+LOIEiF5WHlyO8n9Mc+v58lAbr311g5vLQMwKugjlYiGq1BZtQ6bt76HxtZ2NBD+lvojaK05Su+/D8sXPU/vvxJ+ev9InAYUD1Lt1+E1phwghOrqGfjrX//aJf7PjQJnLzn4s4jqalSurPqdbKBnU8Gvas477rjDeHtr3t722gx3otMRCc1G9YwG1NV/jcZmoL7pJJoaDqCl5jBat55EavP3WLLg93z+IoRjjPnjfA3CH4tzBEivDMsQ9Jp33303XnvtNTNfba9H5OTsJAd/N/nkk0/MxhKFMGeS5NqaCb8AzQZ/NDwHM2ak0NC4Cw2Ev6bhBBrqD6LZwN+OHY3H0FT3AebOamGIM4/gVyGasIxAI0CMBmHWA/iaWgRT81utPOfAPzfJwU+x4VGxU11tHYpLik3IcyZJrq2CX9OcWuCyvXNX+KsRCc/G3YvuR1PzbtSlgC117aivO0L4FfqcwPb6Y9jZtBub1ryCymQDAv75NII4cwAf4VcekTCJsEYAva5motT9IRf/n5tkhf9q681pw//CCy/glltu6Tan390AlAP0XOySsaiU2e7I1hP+GYR/Flat+jWaW/bS6xP+eqCh9jiaahnzM+5X7L+9/ih2NOzByiXPw+9bgQDj/1DMxzBIC2CaMVJBnFURqt9VWVmZ6/5wjtIDfq0iXo2eRKva8+fPN6GOQLagFviZszy87yH40o7HrGRY/2bo0KEmHMkGf9J4/rlYsfwxpJos+Lc2Ev6GdqTqaADSmmOM/xn+1DP+r/ka8+Y+SPBnIRj3IxjTAhjDoGi5Ad+O/zWzpOa3H330UfovycmZSlb47WX0K1nkKe3aHYk2j6uleFav78mjyiCKrcdOAb+SZHuasyv8vB+sQCKyApvWvYzmpkOoaTyBranjqCf8jfVUhkCpWmoN0FwLtDUeRu3W/2LW/E3wM9kNxMII0fNHjOe34M80gNzur7OXrPAr9LnSReDb8H/88cemJEHdlbsmuWn4C/oSeD7uHMD7HAmMIXTCL1XMb7ckzwZ/0BdHVXQr4f4Mrc0nUNd8HDXNBJxGUM9RoIHevkFhELWxDkgx/Glt+ho1dc8jMX0ZvHzNIOP+EBPfSHrmx9Ywf4d+569+9avcJqSzkKsWfkFiTxFu2bKlYyO6qjY7oRb8Hrg8+VQC77I9f1f49e8E/w033HBq+AMJlEe2onEL4W8h6IS/ruUIE18mvQx/jBojoBL+xrpjaG44iJbmb7BoyaMoDVfBn5yCUMKPCIHvrkF6f7v7W07OTK5a+G155ZVXTJ9NeXzN1mi6UjBLbbgdLqdRj8eNAqqullrPk+rf6fC5rtBnwB9MYlZ1Ci0N36AlRcBT9P4tx1CbOtkBf1362kAjaGw4Qe/fzue3Y8vWj1A1ezNKI9PgV/JLz98d/lg8blZ/tc3SLn/I1QCdXq5q+BUj66ggeX2tztraCbULLjehLyqBm3C7C/NRyMcK3FZNv60yEHVsUOjU0+un4afnv/uundje/D1aGun5Ge7UNneFP1MbG48jRQNo4ijQ0nQMGzb/HfHpd6MsHGESzN/RDf6oDEC3+ft0+IWmbQV+buvjqeWqhv/hhx8yHlteX+GOtDv8+ZrFGXEL9QYT+xfK+zPx9Xg6i93sOX51ZT4V/AF6/gXz70NbUyf8dYS6jrd7wt/OkeEwUlr0YhjUbJ7/DZav+gNj/nnw8zVD9P6Wxs1qcCb8Kqd+6qmnzN+Y8/ynlqsWfk0Njhs33vTXLClxobAoj/Ar5veggB6+oNAFh6c/3CW3Yfzt8zFiuJcxfwmKXINRSC0o6DQUGcCwYcPMrqse8EcjTEh1LNFsLFvyR2xvOowWJbX06vWpY9STJtyx1YJfsB+j91foAzQpDKo7gtqajzFvQRMC0UoaAF8zliT4SXp+acIYgDTEvEOHX7zzzjvmb800AN3OGYQlVx38diiwfv36jmnN4v5OFBb3QSFhLix0m9sFBfToheMwasxqTCttQ0lxBG7nSMJPdQ/n84rNSGGPEqNHjza9erLBH1KhWvgerF/9GnYy3m9RQttwnN6d8BP0TPhtA2hoOMnn0AgIvgygseakSYBrav+FGbM3wReeSfgr0uDz9Ql/RxjE9yBD1N/47Tffmr9byb3qgHLwd8pV6fn//ve/m00nBvxihjAE3YQ9nkE0AF6L8unlB2DgwJmY5n0Sk6fcz9j/Drg9xSjyDCD8Q7rAr7Bn1KhRp4RfNfrB4FKsW/k67iPYrZrKVF0P4/pTwy8DsTRVR0Oo5QhQfwLbWvZj8+ZXUFm9AYFIBcKJKDXWJQnW1Kdan+j9qLucZrYEvH3NwW/JVQe/du+oMZT25CreLyoqJugMYdyDqMNQQLg97hIUOG7HbTdtRzj0Pm67vQX9XCPgKuCI4GbCy/AnM+zRVWURWt0V8F2K2gi/4v14fDVqNn6AHYRZ8DdrZZdhTYNAF/AcEWxtoDbyMaMyAE1/1ssA5P2BndsO4t57n0QkvgjeYIhhUAghbXxPwx8Kh8x7kfdX/U9m89sc/J1yVcGvoV+eUJ5asb48v9Sj2Rs343v3YMI8FO68mzB64DJEp76OSPAL3DR2C/q4BsLpIfwuJ5XQuztnezR6aJpT0GeqDb8/mED1jI1obfoC2wiyBf9JNKUY0wtwwX4KlWHIAAz8/HdNHAG2cbRobfoKc+buRKmvCv5wAMEIDS/t/UPa+BKiQVBlAIsXL8H777+f/hRySbAtVxX8AmDSpEnG63fW77jgLnDCU8j7niJ4GNMPKU4iOP5pVPn3Ihz8FDeP20D4h8LhLCD4TIqdhF5Gc4bw+wj/9JmEv+ULtBJmJbyCP8Vk90fh19XAr1CJBsPQp6W+HduZL2xY8wYqKrYw9q9EhKFPyHj+qNkIr11flgHofUSxdevWjsPvcmLJVQO/+hHV1NR0eH1dbc/v8jjo1fOR7y5AXv44jLmxGUnfLkRK2+Et+wjDb1yK65yD4XAw3CH4hVrwSsOvf685fhlVVvip/lAVZs3fhqamb03yahJYJbSNCn1429Zu4HeoQp+0NnEEMLU/HAVatfl96VOorFyLWGIuvX+CXl8hkJ+3fQZ81f9rClS5yG9+85uOw+9ychXB//zzz+PGG2/smOGx4dfVKYNwutAnfxCKB8xlgvsa43Rg2lRg8uQPUTBwBq5xFNLzMzxy5dH79yX81r/XGoGmOZVcCvQe8Ot2ZA4WLvsT6lK7UVfbbsoXNJujis5MsGUItmbCn/m4Fr2aa6zQaVvDQYZBn2LV0idRkdzI9zwTAQIfjHiNWhtfrL3Eej+zZ8/Gq6++mov703JVwP/tt9+ath8CX41kLW9vqZvqdOcR/Hw4PHfgzkmPI5E4jDIfMGXaSUya+jYKBydxnSlxcBH+fqeFv4ca+Odi4fInUdu0B7V1x1FHz19H+OsaTljQ874WszIhP5V2wt+OtvqD2N64iyPBB1gw72GCfzdDrCT8Eb/ZABPi7w+n4VfiqxmgtWvX4pNPPk5/Mle3XBXwP/jggyYuN8VrBLY7/A568+v69cfI61cQ1g/AMB0+P+ANHsUdU16Ee2Ap+nj6wuF2pOHv1wG/XcqcvY6f9wV/dD4Wr3o6O/xp8I128/7ZVM/TOkEr437Bv61hD3akvmH8/xKSia002hnw8XcHYoz5mfhmwi/V+1T5857duQ4dVyz8drny66+/bs7H6tO3jwG/wNUJvzNdl+/IZyzvLkPZ1KdQETuEgI+xvv8kApH9uHn8Y7jOMxp9C37GUSMPHqfg55Xwu9KvpY4NNmAGeKoMQTuuorwdL1+INVteNi0Kaxmz2/Crlj9F4JvlzaW6ndZs4Eubqa38d22Nxwj+YWxvOICdjfuwg/nEinv+gmB4KbyhJOFn7B9j6BWNm6ZZ0mSygvCHkYiX48m/PGnifzv8sUOhqykcuiLhF/haxdV2zCVLlphwx8zJZ8DvLCD0BYz39ZjzNowZVY+o72PEQkcQ8B9i+EAjiH6Dm8bdR68/GHkF/w8T3L5MdvONdoffhl27tgz88rgELhyKIFGxCJsbXyP8+y2Pn4Zf05emdudM4U+1ozl1HK2NRwj/EcJ/xNr2SN2ZOoiW1MdYvPQh+OOz4YvJ+9Pza8tjGn69t3hcXeGiuGvBQjqG/3Z8Xjn4KVcC/PaGjr/8+S9mX61akBQXl2TAX0joi5HnKUZf1yAMGjgPvsmvIlK2H0HfYcbvBwj/AQTCH+GWsXVwFA1GfuH/C7cWuWgAHo+SZgt+zfjYLcmjUQt8NZiKRkPGGMKMwSur1mJr44eoazrcA34T79vwyxCk2eAn+KnUCTSljtEAjqGFnr+l4ThDnxNGW+qOYUfLAdTV/RdVM7diWqgcwWTIdH5Q06x4lNCHoihPVBjPP21KqWl+qx5FEht8e8S8GuSKDXtUuCbva09rmjl5Amvgdw1gnD8Efd0j0LdoMm4e90v4fXsRKjuBoPcEbx+HP3CM4c9buHHE3QyRhsJdpA0tGkGuoQFcx9dTyOTqMc1pwx8h/KblYGgW5s29H3WNP5giNlO4Rrg7ShgIfUqlC9SOEYDapJmgRuYEHXrcUjNDRKOx1WyB5FWvwSS4pWEf1q97maPWEpRF/YglOfJECbw0Vm4a5ibp/f2+AI08iF/84iEcPGiVP9sjpm0I0itZrljPrz6b9sYUhSZSrcoWuIoI/yDkuwfhWudoFA9bgsllrzHUOUr4QfjbCcZJwn8cId/ruHnkfCbFg1FQJC/vRKG8f4G8v5Jdl9m0rlkUgW/Pq4cj2mzOBDhCzx+YjbmzfkH491rlC2cFfxr4DrVmh7ooRwqz+qsRxLzOMbQ2f4tF9zxC719Fz0/go5Vd4JeGgxFMnjQVCY4Ezz77XEfRmyQH/2Uo9pel3VlKcjUTo1i/E/5CxvfFcDsZwzuHwNPfh9tuf5whzrf0gscRIPhSG35/2b8weth0/rtiU+Ls8aj4jQZEI7Dgd5ppTu2gsuG3DKAT/khwDhbd9Qhh39cJf1rPJ/wmhOJrpGo0EuxFTc07mDV/O8LReYiFy1Eer6LHr+owAIVCSn693gAWL77HlD/bIU8O/stUlOTqMInMWntL5fUJLz2/y6mwh0nurbWIRT6j1z9CCI7Dx7DHn4Y/SPinTnwOQ2kgbu3mKnDw35ZQ+6PAbY0o3eE3Xp/JZDgcJPx+RMIJJGMLsWHNk2hsYjyeAf55g9/WdPij6s+GmuOor92PTZvfwfTpWxAKJFFRPgMVyWqOAOWIR6jqAqGEnO83EAihtra2Y/ozB/9lKn/5y19MFwWHqd2x4afX5rWQ8X4hb+fnF6K4qBL+af9GjImtv+wofIKf8b7PwM/wx8D/NAYPmMqcoS+TXcb7boLPXMHjHkj4Cwz8Cns64Rf4Wk214NftZOwubFz7196Hn89vIPwNBn6+vrTuIFau/J05+0tHHcViFYhTY+r9k4ZfM0CCX8coPfbYYx2TBTn4L3Hp/gVp47ZmWBwOQq/YnmGOgV/dFtSBwZ0HJz22w3ULbhq9DYnAfkS8R+EvPUToD8PrO8b4nSGPgf8I7rzzDyjpfzscbsGfRy3h6w2mqgLUquMfef31Bn6zmNWhNIYINRRDeXQZNq99GY2pI2cFv0lsG7NoD+htJfwKf9LwN1Ib6k7QiN7FokW1CIQqEQwlEY1VUysRzYBfSboWv2bMmGH2OtiSg/8SFtOh+ERnnKok1+0i3HnF9M6DqSUmNvcUEtzCPujr6YPrCq7HyBvXIOh7DxHN7pQq1NkPn38P4T9MI7Dg99Mwxoy9H86CkXAW0nAKZUQ0KE8xjceNfIeDr1uA28aNY5yvGJ/QM84PR5j8RsqofoSCcVQn6tCw8TPC337G8GvqUz/LfK6t2cGXyjAY9ui2jIevp0ZYO1v20xj+hTlzNiMQnEXDnEX4Z8Da/cWcREVv0mjUlGio+5vd/eFKlyvG87/26msYd9s4OPKZ5HoYlrgUmli7tDyE113YD9cR3n4DApg49Q+IBr9HaBpj+1LC7j2Qhl/hD8Gn9w/w5zff2oI8GpGz0Emlp2ce4SLwamOS58g38I9LlzJretOC35uG38cRIYbpsSY0bvyO8J88O/j5czWzzdTTwy9Nw88k2MT/qv9hqHR/6wFsXv93lCfv5d81ncBbs0BhQm/Db1d+ypBbW1rNQXxXulz28EuOHD5iklzV7rgV1xcoIdUWQ3VXYwhU4ISL137usRg5Zgv8odcQ8u9GkPAHphF2E/Mz7ClrN/AH/McI7pe48Zb6LvAbAyjiVXmD04GCoiJMUEtyhg06PEJz+xFCH6EBhKj+YBSzKlrRvGUXYT5Lz8+fnz38lqY082PgP4ltOv1FNURbd+GeJY8hSM8fZMwfjic7OkBoC6RtAAp/tAfhySef7NL25EoMgS5r+O2puSeeeAKDBw9OL2ip1l7e35GO9d2Wx3YNwNDh8zHN+zLj+S8QpLf3y+uXCn5eqd4ymLAn6D+E0tL3MGjoCsI/iNC7DPjugk5VdejAgQM5SvgYOytujtAIQogx3ImaikpqOI6Vix/Fjob9qCeAFw5+vkaGprT5XaXUW9/H3DkpGsAcAq/9v/EO+O0tkPHyJMroARLJpKmLkuhzvhJXfi9r+CU6nEHn3qrPpmZfXKq8ZIKqVVg1mHUR1HyGO0VFN2LiHTsYh3+HgO8gAvT2HfDL+1O9VB+NIOjfz9d8AwMHL0a+eyBDHRe1G/xMdgcRfiW7dshgSho64Kf3D8WxZtkTuL/p4EWDP8XXUvzfTAPY1niQhvA2Zs9sQCg6E6FEIgP+aFp5n55/Gj/TdevWdez+ynn+S1C0O0vQa1ZHQFqeP4/wq7msEw53EfJdIzDqeiZ7/n8QfEKv+XyGOALfJ+BpBF5CX8arPH8osA+lZS8T/jn89wMIu6sL+Db8Gm0Ev6o5TVUnvX9Mi1sx7aSihqfj3uV/wY7mY6hnKCL4BbytArWjMa2gz4BW8Gcaiq3dQc+mPeDXazP+197fB1qPYsPafyBRfi/80QoEE2qAq62PEUJPw02E+b4Vvun0Rz8efvjhK3b312UJvz0Ev/HGG6Zfjt1u0IKfCa66MThLeHsg+vUbhuLicnhLX0Q0tJfQa+VWC1raokhvTwMo9R/FFP5sGqEP+I8jFj6ECXc+DmfRVGM8bibNAt7UB6VVv0s9PqOEJBGLI65jRiM6hCJMQwgQpCgqKu+l93wdzYy7bTAzAVc5sx7LNIbzrZmGoII55QCtqf1YtOh3mFI2E6XhIPwxdYAIIpCYyNFgsoFfG2HKvF5jBM8995z5vK80uezgF/jyRDosu7q6Gj//+c9N/5xOz++Cxyn4+8PpGAxH/iTcfAPDHf8PZvXWZ8A/bpJbG/6pgSOYFP4OU0PfM+Q5Ru99ELdPfIhx/jiGUXztU8CvdiXd4U9GVEWpE9MTqKzajLUb3keq2QI9E3xbtXc3m4c/X8bQPf7XhpltLQyjaj7h+2vg3x4l/H7C70MgTvBj02i4OgtAs1eW99dkgs4qu9LksoPfjj21GqlwR7X6JSUlpohNe3EN/ExG1WXBmTcCg0vuhn/yGwiWHUHp1BPw0gC83mPW1Yaf3n5SeB9B2MuwiJ4/tA/j77yP8N8Kp9qaaK0gA3wb/jFjTg1/OJpARfUWrN/4gTlv95KBn6oNMTtaj2HL5lcRLV+Kyb5SGoDXeP+gCX8s1QyQVn4V2m3bts00AbBF34Otl6tclmGPvJAOfrv22mu7AGmVMqiRLGF1DMDAwiDKJvwRCd8+az5fszpmBZfen1evDxzagWn+kwx7jqE0eISevx1h3zcYddNG5HlGGc9vw6+iNlPYxtCqmMZWOnUqyhOqkowbTVLLYzIGTRcmMWdeI2obvjAwm6rLLNrb8GdqpiG08Xdsb96PteueRKzqLpTR8wfjBD2WTMf/gj+a3p0WMb3/f//735uFRYlG4EwDuBwN4bKDX7Un6kGjDSoOZ8+jQj2K+fPdKMy/BWNHbkGi7D3EvIcQ9DLW952Aj3D7/BwBCHwn/MCUAGP/wAkEaRRh75cYdcNKxvtDOYqoitPSTvhd6F9UzES5DBUZ8JdH46ggNAb+WAJzF6RQn/oKdYIvA7xMvVjwS9samQS3fo17Vv6C8EfhI/zBRAXCZtanE35pIOA3YebLL7/cAbk9BZqD/wKJTh5RCxJrhkcnpOuqxSwXNZ+3HcjvV4JBRUn473geCe9uevLDZmuiX9WbBvxTwX8SIcFf9ilGjV5C+Aca+G3oM+EfUFzCkcSbBf4ob4cJThXh34m61DenhF8wZgNf2vvw6wDsk2hrpjOp/S+SM1djaiTJuD+BcJzw6+R3Xi34tUEnxNHSa7o/fP755+a7yMF/gUQf7FdffYW5c+eadiEKQ5yuPIYl+TSAQrPLylXwMzh5dRaNx5jbtxP4z+CbqqlNenvV7ZwKfl6nqluDQh79bOLbGDSgEvnO9L7ftNrwe5wuDB8yDOFAsEvYU864v0KxP40gEb8bS5c/icbmPWhsOWk8fHcYBXg28KW9An+HnkSq8Sj1iLndlNqPVev+hlDFckwNhhFJBGi82obZCb9U+xR0f+d9O83plfb3crnKZQO/Yk3NOevERE1tSh3OPjSAfI4CBYRelZc/J7DFGDRyASYF/gVvcJ+Zuy9jclvm3wdv4MAp4Zf39zLxjdBASu/8N0qKw8h3aM3A2voozYR/5PARCAdDSNJT2vAnmSCWE5hEJIFkYgVWrvw7Ui37kWpTL/7sJ7CcSnsD/g5V///UYTQ0HeTvOYlmvrfGpq+xeOVjDHvU+U3TtdqQr4OuO9ue6LZqf9QD6c9//jNOHL+8T325bOBXn001Xe3Tp4/x/A6HoO9r4M93qpuaCy5HEVx5d+DWsQ8R/O8I/HECTcDp9cuC31L39IDfS/hLeS3lfR+fH6WBTJv0AuH3WiMMQ5we8POx60eMRIieP6HFLXr7uGZGMuGPr8CqVf+4hOE/gvqmQ/xdBJ/vLcURanPDawzVWhAMzEQ0rJJnGYHUht9azNO2zYULF+LNN99MfzuX5whwScNvf6Ca01enASW09ly+1GHAVye1IuTnFcFx3Q24cehaJrfvGZDLNKMjyAOH4A3tMiNBNvjLfBwZtGGdXj8W2o0Jtz0Ot2s8XM58E99nwm+HP2NvTXdsoMZMaYOgj6KcGgvHUVWxGls2v4Gm1gOobz5qIMsG+am0d+Hn6+sM4CYdjqGCO5Ve6H1+iY2b/oGZFTUc1apNnK8FuyjDuGiknKEQrzQAzf8HgkEz8aBueBLF/hJ9Z7Ze6nJZeP5nn33WrORqTt9e0JI6mfA6eHU4S+DMG4KhRXGEJjyNmOrzCbWBWwYQ4AggAwgczQ4/Hy8L7kcgcBhRjhBjbtzOkOdGGlgeYc8O/4QJEwzwVjmz1aEtRk3wfiwYw4zpa5FKfUDPf4BJL73spQQ/Qx1VmdanOCIJ/oYTqG04yushNDV+i40rn0ZV+TKGOAFEYqpS1aaXSt626v918qOOPtUooLN/7fKHy63zwyUP/9dff41Zs2aawrXMnvraSaUFqHxqnlZz88di8m3NmM4kV5tUODKn4c9UhTbWVKe58jEZiYE/tJfwH0I09CluvaWBifQNp4Rf057aIC/gbfjNvDhvx6nRQBwzp2+ih/0fUoyr65ouMc9PbTDvR5qGv55adxJtNIgH277D8sUPIBjUuV9+0/UtrNPfO44+skY6rf5q+tPe/ZWD/zyKktwHHrgfAwcOotfXNKY2paeV0LucQ+j1B6Nv/iCUDJiHgPc1wqeOa4TaqGCX2veBAA1A7Qitq+7z8QANQQtcNIBI5A3cdNNquDw6tkgdma2Whpr1MQtpvK+TF6dMmUIgwuYUlI4VUXn/IEcB33QsvutBNDfuYjx9jPBbxw8J6DPVbMCebzW/i/CrW7QK7+rT06D3t/Ha+Anmzm+GL5KEN1qGsvA00/7Q/lvtv13xv7riffDBB+Y7O9meg/+8iNppaCW3b181i7I3qNhaxISXRpE3jKBOwbjxjzEO3UOI6eEDAprQZ6ifGqAhaBGru+pnvuAJBCPazfUCBg6pRr7ZCcaYn55f4BsDIPxOlxNDhg4xS/469VBFYB3wSwO87Z2NFYv/gBaGEUom6xlfn37/7UVU875omNr/K1UVKA1g53Zgy9Z3EKtai7KED97YJATV/zP9t5rTXzTKcQTQDJBOsd+zp2v3h0tdLln4VUei0wQdDsb1mnLsAr6lToY+ffpcj9EjNjFc+YBfxhGGMIRfXj4D/DOFPxTZj0mTn4KnMIQ8tSgpdDHUsaC3VVsYhw0fZsIds2/XhiGmnVyE38/7ZbOw/O7fXx7wp7UD/rSqAG572zEsX/UUQuVzECyPEH4CnwV+1f/o89DhF0bIfQ7+sxT7A1Ps+Kc//cm0BenbR73wNb2o5lNayU0rw56+fQtR7GEMOu0/qIodZox6zHh9bwb0Pwo/Y38/wVd7wkjoCBPZP9OopiGfeYQ5mjQTfIeDjzsw+sYbO+L8LvDzsXgggcro3diw+mm0NR42YNWbliMnu8B26areK7VWtT9AS/N3mLdgJ4KJ2Qgq0eXfqb/V/N38e/U3295/1qxZePvtt813aNcAXcpyScKvlVzNKXccH+Rk2OFUJSWVEErd6rzWbwLGjtqG6aE9KA8zjmfCWhbUrM6xM4efGtA0J5PeCI3g9vF/IvwTke8oQZGOJRX4NALBr/cj+G8eMyYr/OFIDPFQBaYnl2Lz+ueZPFrw16UYUzOJ7QnapagaodrNJhidHba9mYnwlvcwa24jQonKLvDrMzCfg6687/V6sWzZMgPV5SCXXNgjA2htbTUNYD3aNUWv78q34HeqTJleX5qfPwTDS5YjNOltlPuPIOw/SoD3oSz0PbzBg4SdHj0Nva3Z4ZfR6N8eQzTYjgm3/5Gvf7uZPi0u7E8DKEKRzuilmpVlev+bb7nZeDt94V3gj8YQi1SiIrEcG9f9nV7ziNl+WNN0OcFPJfQGft5uZQiUqj2AlaueNtWf2vUlA5CG00ZgG4JCH20p1eEXmeXPl6pccvDrzChNIwo0eVt5e4+jGB56etXwOApK0Nc1GJ7+fky8868I+fYj5D0Csz3Rf5Dg76enP8pwpifogj+7tpvnR/yHcOuYB+Bw3wgXk+nigiEoYmKtEUCqmR5NdU68c6IFf9rzdSrhD8/AvJnbUbvpY8b5x7GVMf+WJs2nZ4HsEle7C4TaH9bVfIqFi++HPzYd3kiI8Ov0Rxl9Z96jKVB1f9D8vyl/SHd/kEM7lV5MuaTgl7fQtJnZiE7QrFi7gMAxwSX4mtfv6y5Bn4LxGDmmAYHwZ/DR43up5qr5enpwv98qTc6m3UcDa0QAQtSI/wfcdGM94R/O30n4PYK/uAN+hUDFDIFKp5Vmhd8cSBGehbvn/RYNW/eZufQtDHkuV/hN8lsr1aEYB7B1y+uYNa8RgfgMBAh7MBYk/J2zXVJ9LpoJmz9/vpmtE+CmuVi6AvRSqgK9pOB/5plnMHLkyA6vb7SA3rZA3Rj6Ef4CXJM/EO6BMzGl7HUEQulV2wwt8wt+evIs4EsFe/d8QN4/rO2LOnD6pk1wuIai0N0fxS6GPR5BX8AQyIK/iLdLp07L7vkZ9kR08uK8Jwj/fjPTs7WZ8DdrMSk7YJeyWvC3p/Uwmhq/x4aNr6Jy5lb46OUDiTKGQX4aQecskP1ZyADs8gdBnoP/NKI3IqDk9QW93WVZ3ZELCn/G29cw2SxGvmcixt7+K4RUrlB2AuqvaXpsEl5Lj5tFrGzgS7vDr/sm5OHrBb1vYdjQxXA4Blkrugy5CtP1/Mbz8/awwUNMQZsK2VTTY9f1SHX4WyQyF0uXPIkWlQs3nUQNwd/arMWk7IBd0srY3+r8JiM4xvuH0dDwg4n/o+ULUBoOoCzs4yjAMMje95s2AoU/mgFS+YN4sg0gE/wc/Glpa2szwOvAhw6vb4zAgcKC/+PtnzMJHY7hI1YiFPyAYUo7yqYdh7Ufl95ep6mk9VzgjwYPwFv6Mgb0r7YOqHP1RaEOn6MxWvU8Cr88uOH6UdZ+XVU6qppTSa4MQTEwY/5wZB5WLX8W25pPmI3rBv6Wyx9+tUBvqDuGVINmsD7F/LsewLTATJTxb/YTfKkMwIZfm+C1+ltZWWlqs7p3f8vBnxbNDasTQr9+1oknXeD3qPuaGlLlYdBAL0onP0VQ9xNY7cxiqHMW8Cu8OSX8ob38sp7DwEFJ5DsKCf819PzXEn4Hk23Cb9Ya3Bg98vqs8Guzd1AnsUTnE/7nsK3pOJoIf20r9YqA/zgfE/j70dq8DzWb30NVdQuT31kEP0K1vL+gV9sWtT5R7Y8MQM1v3333XevLbif8l0gJxAWHX39wphc4dOgQFi9ejGuvvQZuxvWegjyqFfqYXpscDfILC9DHfRNuGVOHZPQLhHwMUXwHCLPdV9/an2trNvjtmR3B3l31eCT0He6Y9ADcRXcQfjeh79Pp+VXYloZ/zC1jkIhr84oOeZMBqMY9bsp9Q+EKlJevwab1r2M7Y/3mpnbTuUGnqF+W8EsZ90t19leqQZ7/CJqobU1HsX7tOyivqqMByPMHLPhjftMAV60aVfZslz/X19cb2CQ2+Fc9/H/84x/NnH5+PsEvVOdjG36NAAVwFRShT9EIuIfOxmSGJZHQboS8BN93JO3pdZhEV7VBP1MN+cDX/Qo3j9uIPs5hhJ/AOxwoYgimAy0s+K36ntsnjEcykWTM31Vj8SSCoZmontGEVN0n2N6iHVIn0KydUvSgKhjLCtdlol1br5w0awAt/PtWrXoJgfgseKPq/RMg+D56/gShrzDeX3mAjyOAkmCVP9jdn69K+DPliy++MLuzVK6svvoej/rpFxvoNcsjA3C6+6Nv4UTcOGEH/OFPCf0PhFXwK9TpCb40G+CnU8EfJfxjbt+Ivm7BzySb4Bcp3LHhp2r6VWsQiSzwRwV/eDaqGQo01H6CNnn+xuOEpN2slF728HeAb6kMupWjWX3NV6ie2YzSUAyBWBnh11kFFdTKDvhV+6/FLx1+8Y9//CP97VsGcDHlosGvP1znQF1zzTVma6LbXUTAhtEIrCN/1Fffkc+QJ+9GDB25CqWBVxlDfo+Adx9hPcirQhyGLVk0G+Cn07A8f/BLjLrlXgO/jjQq7Aa/Qp6i4iLceeedJsyxD3aWCnzT8js6B/Pm70RD/WcG/CaGCc0MF9R8VvBkg+pyUb1/W234LQM4hrVrXke8YjXKwgp9GP4Z8KVRjgIRA3/AHzDTn6tXr8ann37awcDFlIsGvw6TUJIrr2+2JapTQv5gU7Oj6U13QSH6XTcURY4EJt3xFIIB9dnU4tXBtOenh/eip6pGPwvgp9OIWeT6HENG3oM+rqFmxqmAoU9m2OPm7cFDBmPq1KkcwqPQSYu2aodTiDlAKD4Xi5f9CqnGLxj6HCEoR02DWHVhzgbU5aqZIVAb85ntLccY/jxPB7AEvlAFDaAcQX4mSnzt2Z+IkmAagcKfnTt3mq2pF1suCvz79u3DgrsWdLQVV428VcagLYo6RaUPXJ7+cOdNxtgRbQhN+wKBMkItNT14LPgtT9815PFRswF+Oo0EgHDwCwwbvcx4fgt+en6Hpwv8AwcNNJtYdNJ6pufXDifBH4jNwcJ7fskk90smiUepmhtn0nsFw9/C0Gdnm0aEvVi06PcoC81mDhAj/CE6A8LP5Ndqe64FwCj8Ab8pWnzqqafSNFw8uSDwa3jTAoctOkxC3l7hjq4d5QwyADdHAY8TffOGYlDJAgSnvoVY4IQBP2jg523/UQt8gmu6r5k9uipnljIJ9p+dAUSCQOm0d1E8ZC766CQWwl7oYJiTAb+L8I8YMcIM3d3DHhv+aPIeLF35DOHfQ0gIP8Oexobj1oxJN4AuZzW9fwi+tDnVjtZmK7ep2fQ1yitbMNVfbVqfh5J+hBJhjghMgPX5mBEgAK+3FAsWLDBdtiUm/LkIEdAF8/x2fKc+m0p+1GdTlZIm5KFqJsWKrQuZcA5En34TcPPND9Ir7zd1N0GGM5kqaFW56QsS/BChz1CfjKUb4KfTCF9jwu0vIa8gQs/fHy69F2ch4/4CvieP5fkZBilM08YNaSb8UX65IRpEeeV6rFn7LlJm88oJKg3AqO5fWQZgayp1mLoXzTRyJcCb1n3Az6cWPsb8wXIv4Vf9j/b/VvBziiAWV0MsVX+WMVRabcrX5RgvRv3/BQ171Gezrq7O8vIeDwYNGmRWddVTX+0GC9x5hF9lw8MxfNgq+MreQ5ReORv88u6CXLCXhY+iNHzEaFnoqDGIbJCfSiPhw5g48Tk4irzo52HopfdCIyx0KglPw5/vNOf7ashOJrvN9CQY3wr+ivW4d80HSDWfRIOK2dQeJK1XKvyNqaNINe1DExPfloaTuG/bYaxf9wKhvwdBTQQkdOqjDsFLwx8L0PtrBxhDoXAYDz/0sAFfDbAudAJ8QeF/8cUXMXbsWOTnWw1m5fkFv9kfW+BCSVE+XIRsUH8fvFOeNSXGCnW6g2/D7yXkgt0G/+zh1wjSzqR1D2697RH0K7gN/XRyY4H69Qh+lTkwFFPi6/bg9vHjkaCX1xdnJbu6zWtCcW0cVdVbsG7Dx2hULU8m/Jf4FsafpBrVUgdN+8Nm/p072o5iW+uXWLDwlwhGltApzOPnM5vgE36zEq4q0BCS5VoXCaJ6RjVeePGFNCEXdgbogsG/a9cuzJkzp2N2R8BnagG97YASN4rdozBhzBbE/J8grDNxTZzfi/AzdIpGv8aI0bW41jWc8F8Ll05bdxV1gb9/cTG800qR1Fa+QJBeSz171NKDX6g50yqO2XMbsLX2KwO/6YlzVcCv8O4I4T9mvH8rR4KdrYfRUPshZszcSQNYyph/DiIcATRCGkfBEUAaZvgztWwKFi1eiE+/6Dz84kIZwAVLeB955BFzhpU1p2+dkpgJv8flRJG7GDcMqUJ40rOI+7WYxcSVoPc2/LHYZxh141pc5+mPvML/18w2CX4dbZQd/kAafhWyRY1HU9I7Z34K9Q27LPgJvPbuWnolw8+/jd5fnr9J3r/+GNoY4t3fdgzr1v2Ln81G+EIzaQACn8qRM6Kuz2n4ffwyZQA19Vu7dH+4ENJr8OsPsP+I9957z5S4Cnyn00HPSvXo5EQ3lTE/DUF7ZgsLfJh8x2P0+p8hbOp3CChBP9XcvZ8xv0l4tXE9rbp/5gkvDSnYDn/wLQwduRDXuQYQfnr+wuuYf6iaU7NPNE6Hi6HYAPi9PtOPU39Lh+fX1cxnV2PRooeY/O0x9TwW/J2aFZwrRQm76n60qNfUcAItdcAOfgYtjd9j4cJfI15+NyLMkyIJarySGudtfmaJCEJM6kp9pSjjEP/oY491mRXsbelV+CXanbVp06aOPbCmpz5jassAPIS/hFoEh+sWDBnZAm/4cwTDKlqj95aHN14+O/xSjQDWft1Ozfa87MpkOtSOyVNeRGFJEtc5hiBPB1YTfo+nD5XvV33/HU4MH5puV0INBhm3yuuH1bIjytiVX2ToLqxY/iSa1PnYHBt6FcFPNa3OpfVWLZNKOralmPjXvYe772lFrHI2odfJ79QEvX+S3p/wy/trFPCHfJg5exZet6c/zf97V3o97NFJfrfdxkSyX7rVoDy+gZ8qr+8cAme/6zF08AzcPvklTAvuRSB6nEAR7CDoyU8P/09Twk/PP2Xq8ygqCaOPYzDhd8NZqGNM+5n3KvhdTNCvHzGCuYG1R1X9agz8oSSvEQRC9GCBBVi+9Gkz9WfB31WzAXMlqV32IDWlD/T+bdSdzYdQu/WfmDF7E0Of6YSeIaLAtzUd/0t9wQBWr1mDz7/8Ik1P78p5h9/erSPRAcbz5s0z05pmOtPAT5jk9Y3nLyb8N8LVpxQTb7ufHv8LTFPdTuQYb5+w+umEqOmy4/OvIMDtmDj5SRSUlKGvsz8c5v1phNL7LTA9g7TAdePo0VA7wrCW6LvDz5EgHluCtfe+QM9/xJQvd9dswFxJmg3+FvX+4c/aGn7AimV/RrJiibXyq4WvJIGX0vt3qLpCRELYtnO74bC3pdfg1/WXv/yl2ZNrElpTn2+pu5Cxvo70LxjAZPIODC1YjsiU1xAJHDbtwk3fneARJkoHjQYYy2eH96cq4Q+fxG3jHoPDzdFJm+QZ9phQx9XfqLWB3oPxY8ciRtCjIQ7TVBPrhxIcBWIG/lkz16Cx/nW0tBw19fs9tBssV5pmg7817f11+HWq/gssXvxLhOJz4FfXh3IZAD9Lev8wNWTi/xACYR/Kq8rx1NNP9frCV6+FPTq4QHUwAl/HhHbsyTU1+gUMLZjkugei0OXH1FufQHLKDwjpJHQCqRbivuBh+MJ7qXsIl5rPZoP3pyroxU/illseRF7+aDj5XpWIy+O7nIONenhbLUvG3norPT+HaQO+9qvyyxL8oThHqDBmzbDhP5aDP62m5p9qnfx4mOHP+5gz7z7CX4lAOcPHco6k9P4C32yC16jABNgbKMNdd93VUf7QW9Ir8Gsld926dSbB7ei6luH9tUHFUaD24qMwYshaxMo+pudneGPgVz99ef5D9Pq9Ab+mN/m7aGBW2HOUIU0rHHkqp9b7lNcvhNs5iO97gDGEgsICTLijsx9/mEOzvJT27IY4AviDUcydWYdU7YdoaT5x1cNvlI810+Nr1beFCX9r43EaxEGsW/tvJKqXoyzKcFF9fozydlQdIIIMewL0/gGz/VG9WhU6S3pjFqhX4LdPTNRhEpm1O3Yc7SooQb5nKOPsCCZN+he8DHWmeZncahuiaT2iDmqHCf0hKq+BM523/zHVtCmvanPio0Gpr6dvD4YP38CkdgAKXOktiy6GZuneoJqGHTR0iOnGrKZMVoluCOFY0GhIX1YwiSULHkFL3W40ZwNf2g2WK11V/Cb4pU0N7aa0W3sbGhu+wZJlv0IwPh9T/HE6N4aN2gRPDWomjZ+z6QJh8qowfv3rX5utroL/fBvAeYdf5co6sNj2+D3gZ9jj9AxEnuMOXD8qBZ//K3MI9FQmtWo8pe2J6r4WktIQglR56uwwn51q1kiVoIEAf0fwOEMWHVb3BQYPWQq31hk64LcNVTvJXBg4ZDC/IH4ZccamatFnDpnWlr0AvVWACXkFFs3/DZpr9+Xgz9CmlE56pNLzaw9wY722dR5Cfe1HuGvRw5gWnEUNw6dY3+z6knIEkAGEQlDvz9mzZ5sufr0hWeGXno3YszsS9WmRx9ch0YKnO/xOhhT5ztHo338xpkz8D4LBvSgLHkWpFqe6wH8sDf/58voW/FbHBr526AT1CO6c9CpKimfBcwr4HYR/8IhhpjWH6tOtHpUW/BET+lDDVVh69++Y5O1HKhv40ixwXOmaIvhSrQKnCL7g11rAjtaTqNn6AZKVW/i9J+GLE345En2W2vZI+M3uLw7N2uaq5rf24RfnU7LCL+99NmJvSNcbvJWJ4c9+9jMT7/f0/C44HQNRXBjBtEl/RTy0j/AfhJcQeoP07oQySAOQt+/U49TsMJ+t6pQWr9YONJIwlIpGD2DilOeZkMdNP9BCvk/V70u1suvS+6XePPZWA73dpFXwRxnuRAm/irOSlXOxef3fGNcehHXcT3p6Mwd/h5rQR5pOhLe1HMH6Da8gnryXjqUcwQTjfcb8xvOnwx55f62ryAgaGxsNrOdTesCvkOds4FccpnJUGcDKlSutzehpr9kdfnNaOr3+bTc2oDLyGRIRxvQ6G1elCZrLJ5QW8Lpmak+Qz1bNxhf+Dm/QKoUO0tCisd2YXPYnFJcE4FH9fgb88v5631nh55cUy4A/UT4Hmwh/Sw7+LpoVfmMAJ9CaUv/Pfbhr/hN0fnchqFkfU/Gp0EcTC7wSfhmB+iKVl1eY7g+aTDlfkhX+vXv3pu/9uNhJyAsvvGBakGhDekkJQ4hCLWxph5YgYgLJ5NHpKMLAYj/KJj6LCnrdaOgwoaTXF5RMPgVpT/Cl2YE+GzXwqw6Iv9Ocv0UDiEZ3447Jv0Jh0SR6/oKs8CvhHTPuNgv+tEYIfzzipwHIM8VQWbkcWzf+27Qo1KHOOfgtPSX8DccZ+7cbA9i47l06jzqGPTOZPyUIvzbAW2UjobBqqAKI0enICDT9eT7j/6zw29V1ZypqRqqNyQp35OGtOX16e4/q9gvMpnS3cwAKnWNx+y31iAY/N/F8iGALTOsMLcGfLmMwYUmm9oT5bNXs+godQllE06f7EAqeRJTX0bc0om/ejfT8PeF36n5xEW6fdKeBXtNx0jDj/UTEa7x/ODgdd83ZhlTtZ2imR9OhbnX84qV2aYM0GxxXuqb4d2dT08uI2pI6Qv0Ka9c8j+nT6xCMzCb4lab1iZpehSNqeuU3U8uCXyGQptC1+0uSmWuei/xk+PUGduzYYbykqjY72w1qqlAb0gv4M3r9vGEYNWAJYlPeQiSgPbjtCHgtMHvA71dxWqZ2Bflc1JRAM7cojeyDN7wfIRpUjLdH3bIVffJGosDAb4GfCX9RSTEmpOHv8PyM+S34+eUEZ2HB3AcJ/9cczun1c/B3aDbwpc38mQX/IbQ176J+gnX3Pot4/F6GkXNoANWEX42vCL0cTBp+xf4ygO3bt2P37t1pAs9dfjL877//vjkxUeBbrcVt+HWYAz2+wh2C5MofjvGjN6OaXj8eOcrkM91fk8Db8PuNAWSH96eq4C8LHTc1/16OACH+rkhoF0bedC/65g87JfwlA/pj4tTJHTM90ijDHsEf55cSCc7GwvkPo6numxz83TQb+NJO+I+iLbUX25u/5/VTLLzr1wgEl8EfmslRQHslLOgzVYtf2kaaefjFuco5wW8PN3quVuEEuw5rU8hjr+IaIzBtB+X9S+By9seQkqmYOK4RZf5/McP/EsHwbkJ/jH8Q4ZempyK763kJe6ilDHWmhpT0HjcdG3xTP0bhwJnoZ1qSW50abFWTKo1mw0eOZI7AuDOpDgT8Qqhxhj7lHI4TTMrikblYsfS3/CJ38Qsn/Pxic/Bbmg18W7UCbFZ+Gf9vaziMnc0HOXp+jOqqbfzOZxF+jbA64DtmWp7Yff+lGgHOR/nDOXt+Jbrqszl8+PCOldxO8KkCv1Bdl4sI0iArBNKG8OJb4BlejuvvrMXk0JPwRj9gLL6P4OtUdGsE6D34Qfg50ijeF/xT3jd1/DrBPRN+eX234He7MHLUKARCIcTLtRFDW/C6wh+LzsfKFU+gicO3kl0b/Bz82aG3tYmqEUB1/20cMbfXt+P+pmOo3fAvVE9fRSej1fQwopEkNc7R1joDQfDbIZAOv/jhhx/SRJ69nDP8+qVLly41U5uCX8DbU5yWATjhLtAxokx+nWpBSPiZBPdzO/D/9+Th/0qGwD08iNHjt2JS2Z+YhL7LWO8gYzrG+NKMTSlWPX+m9oT7x1Tw64zeqTIuvgZzVvgmv42i/mHkKynXeyfw8vhS3Rf8o24YbRZc4hxqrT2occQZ+pRz6IibL2UxVqx8Eo3Nu1HXeJXAr79HG3SMWrNbRvkzo+Yx/YzPSxH2HqoZIMLPn5viNxqAKkB30AAebPsS69c+hET5dOjAv1gsSU2Y6U6p4LdrrDQVqvKHc018zzns0fNeeeUVs/qmOh5zRm16YUsdz3Tf6co3t9WK0IbJ6XLQAPqhD6/X5RfC4bkeg4ZMxK233YNp3hcZ5+2ipe9DOERDYGKsqU4DsLYy2noORmDgp7cvFfReICFDmPAvGuQdcNAgXarjZ6hmG7Deq5tGPPa2sR0fvK3qyZ9kQhYJVqGifAvWb3gL9U1HUHvVwC+w1Y7lGOpSJ1BDkLfyb9S1hmDXNh1HHbW+6SQamvl8tWmn6rCOVHM7mlqPGG1pO8HkleC30gCa2rGtcQ9aat/B1o1/wPTKxRxV6WgS6vUjI+j6HUgFv0ppMpvfno38pLBHokUHzfHPnTvXbFBXWUOfPn1NbY9pRZhWM2ee1s7HHTQSGoijn6n3cZXEMWpMI43gGVr2RzQANaw6QVWhmyo7eTWzP+cGv4/hjkmuBT8NYcodfyPgYwk/jTYNv20AWtwS/OPHjze9euRx7A89HkkgHq5AODADM6qbUVP7ZQcEtYTjSoDfdGXL0C4/p5ErvzFhHm/XCHwbfgP+YeoRAk8PT+i1s61O08B1Mpgj2LZjL5rp4esbP0Z96n9Yt/E1LLnnGSxf8gTmzmxCRWI1R9d5/NyTHHHDvGaHX6oEWOy9/977hkfJmY4EPeBXBd2ZwG9+QcbvkNE8/9zzqK6uNkagxS4ZghkBCLrxpl3Az1QH424Hfs5w42euEXAVxzFu/IOE613EQz8gGt5DK9/NkEgnshzr3Nh+tgaguX7mD37CHw8dxeQ7fkfAb4VDi3Fp8G0V/J5Cj2lJbg6fIPz2SSzmQIpIOd/PdMyc1UoAvqG3O4GtVxD8XcqTqT0MQI9RdW2Q6m9McUQg+E0tB9DSuh8tLfvR3Lyfz/8BGzd8jg1rP8XGde9g9b3PYMGih1BV3YBkxSZE4/cyr1rIBHcWQ99yfk/a3kgHk1R3PH7e8ShVVx0E0gm+Hf5MmzYNNTU1Hb3/z2QWSPx+//33XeHXC2gO9WziqMznasP6k08+aTylvL8WvmQAVme2dDhE4DNHAmMUDD3yGA71dbpxXZ9hyM+biqEDFuBOGkHA/w4/nD38UA7A69WhFISeaja3+9qNZoO9q2pzuzo78Ln8d4nwLtwwaqspsnPofRF2qTa02IY6cNAg05U5xuSrK/z88MPawjgDdy24n/B/R/jbsZVQ9Ar86dg66896SbvDryNJa2v4PvizZnpzVa+2MoTZxpBlRxuT1tYTDF0O0CB2ob7mc9RufRMbNz+NZcsfwZzZbYS4BpHwRjqyFUxkqxFgvuQLJJl/TWeON4fhrja4hxBLeKkBhjvMswz0DH2yaKYRaO5fRyD96U9/SlP44yJmlbeeF/httUUv/NBDD5lhSeCrN6egLy7W3L8Fl1Tdj80mEt138HFHIVz5/eHsNxiO64bAkTcWngELMWr8IygNv4lA+Ae+Jj14KcOXsnOAP70lMh79GNdfvwz5jpGEv8BAL2+vdirm/fG9agum4kq119aH3AX+COGPVGPBQhv+kxcA/gtjAPLo9m4se0dWYw0NgNrKuP0+xultrXsZznzGv+19ev63sG7t37D0nt+bNY+KZB1BX4byygV0glUMMxP8zPl5BRgqBpP8mc4sDtEQOKIyfIyGZlCrGePzs41pPzQdTYa3z6aZ8GsEUPWnDr977bXX0gSeXhS294D/6NGj5kE7pj8TyYTfaHunEej0FfVjnzRpkoFKs0NWCxMLMjWEstQDd34J3Hn9eS2C2+GBh6OEw+HEz90Dcd2ACSgeuRBjxj+KaVPfY+iznx78hPH+nYBbI0KHduQGNI6ANsKroZW1PyAWewMjR8+FwzmUwHfOVNkqQx2tTev8YNWUqjv8cQ7PkfBsLFz0MOHfdQHgT2u2n0sJqVH7vnm+uql1+zd6LzIkW2lQit2luq+Wg20M4VpTVve1ttQhU63a0nAAdTW7sGHdh1i98hXcvfgJzJjdjETFvfTSd9MRzEGQEIcJu7Z2al9zOKKpSsbraY0T+gSBjwcrqVUMPSsQk4bLzTUenk7l4xHejpUTcoY+BvaeRmCDb8/7a4SeOHEi7rnnHnz++edp+k4t2h8sJ98FfiWwZwt/DyH7maOAbn/44YfM6lvNarAd62sUyOzUrDIIl1P3rZHBo5MQPUyIi/OQV+BCP9cgxuETMHzYdIy/rR5+NbINMYSJneSHB4QYy5s25lLe7jAAUx/EcInqC6qOvx1lTKoLBtzJXIMjUeY0rVS/m4+pK7P9IXdVjgSEPxFdjntXP0cPuMfMcvxk+G3AqakuhWAZSsC7aF1aa9NX87g2kGgj/UG+lrpEtzMmb0dN3VHU1CsRJdzbTprZljpB3XiAsflRNBH0pqYfGKt/jk0b/2u6Uaxc/ifcveBXmDe3DZXTNyCWXMbYfAFC0dnwhyrhDWoDfxg+jpB+rcKa2idrh1vYFKaF6STCaQPQVafUJ9LKz9KoHiPQURqC0XKUJ6uQYMJrL3DJCWn2J6pdX/4gSku9dHx+E/Lo1Jfp06djxYoVphHy//73vzR5pxZxrgLOLvArWVAi0Bs75/ULdSSljiNS3b89NWqvEXQagaVmP62K4zx94C7oY05sUaOrAs8AFBXejBtuXIVJU56ix3kficgBM4MTIfTGCJgUB+nxgwyJVL6sLZF+dYRgzC/4p5X9kYn1zcijwXk6NtfztdPwF/D2mDFjuniZrvBX8Hfei3VrXiZM+wk/4SLkvQ8/we6i6cdsI7ANoMFqIZgyr8X7jNHr6w/yvezDth0HsPMX36Pt/k9Q3/w2ttT9F2s2/ANLVzARXfwoZsypR7JqNWPvxQbyICE35QaEWnVN2sapjTzRiO7Tw2vjOVVtScyZXGkVtLba3v+0qnbvBvA44a80t32+AEf6UnjLfPzeIgxtpmP+/AVYtnQFGphla57/6aeexttvvW0KLO0tjz8myk21d6UL/BLBfz7rpiWZI8HRI0fxn//8B5s3bca4ceNMTmBPjVoeOBN+2wA4CtD762hSt6eY8bn2AQ+Gu3gSBg9djkkT/op44CskQ4cQMVOiKluWHjVXy/Mr4VWXtpNp+G8h/AS+wDplXSr4tcKrQ6fVUTor/Fp8oedPRtdg/Zp/Ev4DJuzRVJ8N/k+BX8BmBZ9qV0Sa243HjYfX8aCpet4m9GbhSMoEXKcltjScoEEc5s93Myz6HDW1b2L9xuexfM2vsWh5C+YuqkGyejUCUYIepybmws+wTlsL/QQ4FKcHjwty9dXXHgZt5GFimlbtaTA72vjc08EflffXirgNunmMV2qEo0ZIZ3b5eQ3yPkcDlTVUVFRhzpx5WLFsFVKpZjz+myfwwgt/xxuvv4VPP/2M8B7onNkRXp2I/ajISHQ0Ug/4FQvJMnpb9DtUn7169WqzUGYbgcBXbZAZAYwxaJFM0Hd6aDcNwcFYPc9Rwn8zCsWFIdw4Yi2mTvg9k+EP4fMzJwhos4xU8B/tgJ/fFW6/4zH0c49Gvvpx2tBTTXkDc5ABxSWYPGmygd9qrZ2h2nARiGBm1SbU17zFUIGhgxZ3BDohbsiiWWHvpvL2tpqD7Dr0RFoVjzPZpLZSdzJ02b7tCJqbtHdYp6PI8x9HQ+1e1NYodHkH61b9E0sX/AFzZ+zErBm1qJ6+EsnyeYjGqxmaaKalgmFEkp9LOYKMvQP0tmojEiTwwbiAZhhDVU9901c/A3wDP7U7/LovVchjwhV+ZgI8wjxAGvD6+B2VGdXjlckkZk6vxl3zF2L9uo3Y1rYDv338d3j55X/So7+Lzz75Ant276NDPs0U5lnCL68vA+gBv2Ih/eBCiSzwxRdexJIlS8zRP3ZSbMX+ygOYCLukhaaVeUFBPgoK+5luah79THG7YwAKHCMxoLAUo27YgtunPoey8HsIRL7hsH2A8Ft9PAV/PAzcfMsvcI1jBBw0OK3mqqTBePy051dj2tKp0wz8OlMqU83R+ow7Z83YQi/8PlqaDzHuP4l6en4z390N6tMqvbVmV0xoQug7PDxDGWmLlPdbqaYUgL+jRTF7yyFs2/4DY3eGLk1vYvPWt7By9au4666/YvacX2P6zDbEyjehIraKo+EChL1VCPuZvAd9NP5Sqg8xetlYkHAynIhQw9o4bjbm6yBpxu2qr2F4pxmbCA3DeHBCnQm/gZzAC34bfNXhh0IBjrg0IMKta4DxeZjg6+T66ZVVWHL3YtRs2YL7d+7EH37/e7z80j/w3rvv45tvviMPh35yxeaPiXYryvn2gF8LVtILLUq0NVc7c+ZMUzCnMCg/n6GOaoNcAwl/kYG/sKAfE+V0J2VXMT21lIahsInar+B6OIeEMfTm1Zgw5Xf0bv+jp1bdEL0/Q6JEuJ35wnb83DEU+Qx5nHydTvitUWDggIFm8cR4LUJgqQ1/BF6CNHNmI6H9CK3NOprnpFnJPLWXt2dWmHwate6ruEsxe6pOoQy9eyNDFao123KEtzXTQs9et4fP+4G/70ts2vRfLFvxVyy851eYs6gJlbPXIDp9GfzxhZgamImyyAx4o1WYWBZkrMxQxctQxRtAzOdjaOhFguAnQn5qgHlSAHHejvGxaMRHeOmNY6UE2UdVCFJJw5jJn1Vx1ONnkPbqKu6T1xfoQSa3ajQrDdC49Jieo4M81H1BJ+xvXL+eoN+HP//xT/jHSy+ZUvjde/aY3FIxumC3I+PMENkI7+qhkwzljZ6Fhz+VyMFrZrMH/JrrP9sODj9F9Mdn/sFadtZ+zfLycgwYMIievwhOzf87CWahYnQtmuXT89Njq3DOXWhGARmDW7NDDGP6ufsznh+F/v2juGV0HUpvfw6R0ncRmvYxor6vMWLkRlzr6o/8QqcFP4E3BsDX0ZrDsKHDzBqF3atHdfxqWyJVuW0wWI2li58gvN8x5DhI+I9YMTsTTh09muI1c/qxgbF5Q9MR1DceZnh0EHWNh/hvjmFHizqaMS6vPUQvf4DA76PuohF8hpqtbzIkfAH3LPkD5s97mPHvDmoDqqbfSw+8kKDNYBJfDl+QMXowDC89uZcxtJehhpdwlhLGYNCLKIGPBuTp0xoKppWGIVAJr6UEO8zHGdfHFOZopkVz8Uru45WIJ+IcPf0c9fi58LkBGo3PX0ajCKOyqhyz587EPUsXo66+Bg//8kE8w0T09ddew/8++BBff/kVDu0/9fGj7fxPDLSfsM7nspnoUBv8tPLp5yx6PcGv39MDfiW7ivsvtmiN4Be/+AU/6AiNYCBj+/T6AL2/cgJ7erK7aqamkD83IYxzEIocEzC0YCZuG7kFwam/RzL8CgYPmY0+/Hk/5Q7pkgbz7/lvlWeMGDmSXzRDAIFPELR9UQYQUDdherVgpBprVj6Dtvq99MwHmXgeoh6jd2bYIi+eMfti6mOaODo07zNL/23brRKAxtRuhjBf8999ZEBfu+ZFLL3nD1i06BHMmbcD5dO3MGxbRrDnE/JZ8PN3BsNqkUgjVGJIjao9uukbGuXPtNUyyoTV0iDfq7ZcRmgE0mjYb9TaHmip3S3B6pggT8/QSKrXpUGFaCShkLYQMgH2+2lwWn1NYN78uViybDE2bFqPRx75JV566UW89ebr+OLLz8nOLhw+RNC13iOf1s1TE2WhDvp6A73+O8H/2km1oLfAz9TsRtD9dc9UBL3g1+v1gF+/XCFIb8ddZyo6wfG+++4zq3haF1BSrDKJ7tDbWiDwFR55HOZawHzBw/i+0HUrhgyOYcwtK1E8cAr6ehgi8bkOJtJ2TY+bYZCuw663NrHI89s7uIwa+AMIxMqxeuWThH8P2hoOMyY/xlGAyafCFBqC7rcpVqfnb2lgMtrEEaL5c+oXHB20be9NLFn8LBYs+gVmzt2K8qqViJYv4OtWwxcpR1moCqXBKkwLJlEaoGcPqbMZ3wtBtIEMywBMrG4ZgOAPEnoZgNQkq/Lop4E/SOjVJyfA1/QHeT9A7582qgjhj/N1ZsyYYap3G1Mp/EpTi888jVf/+x98/OnH2LNnN9qPH+W3lEH5yRM4fvQIr7xvP5z+kUTQS49TM+HXf8f130l6fr7GyQ7NMIDzAL8iG7t+rQf8ElmGXSh0qchHH33E0KLRTI9q26RUTXDtGSBLBb/Ad3ZoQUEePNpbUOhAPnOEfs5RyHMPQV6hC/kE3+lhSJWGX+opLMDNt45h8ke40mGPUd7WdkY/b8eTC7Bx7StmF9L9TSexgzF/G0OftuYf0NbyDW9/Seg/Rf3W97Fp/cuM0R8m6CnMn1+PGdWbkEysobdewgR8FsoCSWoYfiaZwYQXgcQ0GlkAIZ1lSw1q9BHYYXlgS+X9IwS0w/OnVW0/QtGYUc3SCP4oQ5kEDVfXcNCPEA0gFGZCyrDHTwP3MZSRASSS5Zgzey7Wrl6HbS3b8MTjT+Aff38J777zDr7+6mszCZKVt/bjcqeWKnY/QXh1W/BnEXErlWu14c80AP3XCf75h18hvZ3TZoVfMzBn27zqQoiGLCVLWsnT9KhqhuTtNSIY+AsIP/OBQinzgUK3lSR7Cq+Fp+gauGkAao2eX8CcoED7CQS/5e2lVjVnAcZNuD190Fwn/CbZjceNF04klqFu85t4oOUI7m/Zg8atH2Pzhlexbv2zjHsfZaLXhqqqGiQr1jNMWMx/qwUcq24lJhBNssgwJVzOcKbctOsLxBhWxAl+YjJCyVJziLOmGw3MfF4oXMFwJ27A/zH4deK5ZqWChD3A3CVEwAO+Mvi9pQgEyvj+ozTEubh3zVqGYC34zW8fx0svv4z/ffgxfvjuBxw6eNjA1l3a+dhxktcBaTuVsHfAnzYAhg96sgVot5cRt9KLAb9eQyG9kl1JVvj1Qw0N2T6AS0W0h3P58uW44YYbTBgkVcsUTYOaGSEmvYXOoQx5tI2Siax672t2xzMADvcggl+Shr/T66uy0034x44fZzx9d/hDNIhgLImK6fdgw71/wbpVf8OiBQ+iunoD4hV3I16l/vMVmOyNYOK0CEMWAhvTjIm2PfqQoCc2MytMRCP0uoFQAn7Nr0cY1iicipcR/mkE34twguENRxq18wiFZhF8KY2gG/z2fY0IfsbmPinzFZ1zFWCiW56IYc6sGVi/9l7ct3M7nnjicfzzlZfx6WefYi+9oICWiCdbTh4n5EeOEWximY7DpSeo3eFvv4zgl/PUyaA211nh1x8q+PXkS0nMF9AtF1Eln7ZUanpU+wjy8voYb+900KObdYD+hD+9m4xe3sEwx+EpMlcBn5kvaHp1wKBBmDxlClTNqa10Nvzm4DmFPrpGKxkmLKI3XgCfv4qxc5JemgDHGD9r3pvPDzBM0cnsMR3ExrAiSgOIaoYlrZpZUYtzlQ5oBsm0Pdf8ullV5fP5u8xUq5o5acqRqrN/lZj6/QxXtFhEr65E1Kd5dP6+8ooKLLr7blNC8sivH8HTTz+F1//7Kj779FN68+zT19kcnIoTTYGiDV2mZvwnAs2/l+r5tprHrNfqLnq4U7P/1/1ZHZLlobMRhW4K6W3JCr9ET7qQi10/RTRSvfTSSyY569+fIU26XMIqk+iE23h3hka2ZoN/2DBrmlOrk5pp6oS/q6pzc0deIKNgOGO6OOuxtJrnmpmUU2vHbIv9fKoNvjSpzhF8no7sF/Aqs9Z7UzGXSUSZB+kUnGeffdb0S/1+1/c4sJ+gC8BuIk/aLrCz/OxqEDn0zFz2lPDbWfHl9EEpmdFmGtV2KxlWTpCfnzYEhjR2eJOpmfArdBoyZIiZWbLrUjKh7KoCtiu0ttr/tuM1ugGfqaYrcVqtWRclo0x+VbHI8EXrHfPnzzMhXnNLs1kDef755/EOE1GticjwT/0dCXQBr7lzW60w4moTRTHdK5ZPCb8kMzm41CXzCxUUOvhaHlKl0xoJPIz3VcFpT2fqqnl9e6bINgDlEAJPXlf/Xl7Y0q41PvL4UrPyadRaAZZqY4at5jXSo4iuAl5Qa3Qxu5CYjJb5vAb68opyzJs/37Tle+CB+xmfP9EBuqoWTzv9nIVnK17urlen55dj7D6Jc1r4NeuTGSNdbvLll1/i8d88brp82SOBZnQKCgsN/J1TpBb8Kq5TNadATSQ6W2Zk0w7QqZYxWKrb9nNs6HXQgoA3np7AKyTSe9LSv84p3rZ9u+mD9M9//tOELupHefDAwfMKqQ391Qi+/mZFMd2rlU8LvzzNpbTgdS6ixO2zzz5Dc3Mz4+ZSFNMITKMthkI/Br8K22y1gc6mNuSZ4YxU8bmudnyuRPShBx8yNUxq/fIpE1ETox84YFq996ZczfCriE3wd5fTwi+5WIVu51tkwFojaGtrMydFCnQZgb1aLAPQeoE6Ngh8eWZdFXOrP4xuC3CpgBfUdlyu0MXuIzNnzhyzna6+rt4kor9X1eLLL5vdbHIkij17AHj18XhBxa7i7C4/Cr/t/S+1ac9zFQ19b7/9NjZv3mxAF/gyAhnDoEGDjGGYOv60N7e9t24rfFGsLsirqrTZYg5WrVqFmq01pg5J8bn2KHzw/gfY9d0u87uuRk97KYly1lNN3Pwo/JLLPfbPJprNeuP1N0yz3ZtuuskYgPIClTLLo2tTtMIkQS/Q5zMR1ekz9fX1ePTRR/Hcs8/hrTffMvH5nt17Tr0BKOMzt8MOW3PSu6KZHXF7qp2JZwS/vih5/1N+wZexyAiee+450/nXalIVM4no2rVrzab73/72t8aja0VZlaYKAbOGLhmin2nEtNWeXuyuOeld0Xd1ujKdM4JfouFDU5+Z86RXkshDKAkV6O+9955ZBjfFXKeA1AZYn4et9mOnezxTc9J7IgelcEef/6nkjOGXCJBLseDtQkkmuJlw23qqn2c+nqk56T0Rqz9WmXxW8OuLlPf/sRe9XEVAZoYp3SUT3POhOekdUY56JjOUZwW/xF4mPlUSkZOcXEwR9HLQZ+Jczhp+iTy/YmJ5yZzk5FKRs+XynOCXaGjRCJAbvnNyKYgiEYF/NhHJOcMv0RCjxCJnADm5mGKH4mdbhPmT4JfIAH5sSiknOektkadXi81zWYP6yfBLFAIpybhSSiBycnmIYnyBf65l9+cFfoldOXeubyQnOTkb0QLkT3W45w1+ib2qpo0DuTwgJ70hYsxuP/JTQ+3zCr9Eb0irwDKCK3UxLCcXXuRMFV6Lq/O1t/y8w2+Lwh9l4HqzuQWxnPwUsVnSzOL5XFvqNfglslYNUUpKdM0lxDk5G5HTFPACvzeiiF6F3xZZq0Khb775xiQpuZEgJ6cTTZ4IeDUiUKjTO/kj8P8BToe++pP4VYUAAAAASUVORK5CYII=[/img][br][br]Do svého [u][b]Android [/b][/u]přenosného zařízení si stáhni a instaluj[br][b]- GeoGebra 3D Grafická kalkulačka [/b][br][br]Odkaz na stažení [url=https://play.google.com/store/apps/details?id=org.geogebra.android.g3d&hl=cs&gl=US]ZDE[/url].[br][br][br][br]Do svého[b][u] iOS[/u][/b] přenosného zařízení si stáhni a instaluj[br][b]- GeoGebra 3D Calculator[/b][br][br]Odkaz na stažení [url=https://apps.apple.com/us/app/geogebra-3d-calculator/id1445871976]ZDE[/url].

2) Práce v aplikaci
Ve [b]funkci Algebra[/b] můžete vytvářet vlastní aplety pomocí algebraických výrazů.[br][br]Ve [b]funkci Nástroje[/b] můžete vytvářet aplety přímo pomocí konkrétních nástrojů.[br][br]Pomocí [b]funkce Otevřít[/b] můžete otevřít jakýkoliv volně dostupný aplet ze softwaru GeoGebra.[br](Funkci otevřít naleznete po kliknutí na 3 čárky vlevo nahoře)[br]
3.) Aplet v AR
Jakýkoliv otevřený aplet v aplikaci můžeme snadno převést do Rozšířené reality pomocí tlačítka AR
Hledejte rovinu, dokud se nezobrazí mříž.

Poklepejte prstem na mříž.

I v AR můžete používat Nástroje a různě aplet upravovat.

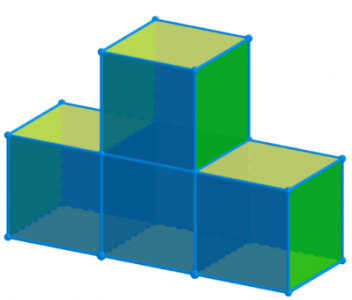
Ochutnávka - Krychlová tělesa.
Rozšířená realita (AR)

V této úloze můžeš využít Rozšířenou realitu.[br]Jak na to? Návod najdeš v úvodní kapitole této knihy.[br][br]Pro využití AR hledej aplet pod názvem "HM A 40.5"
a) Zadání
Pomocí krychlí vytvoř krychlové těleso, jehož portrét je na obrázku.[br]Krychlové těleso postav tak, aby v prvním podlaží byly 2 krychle
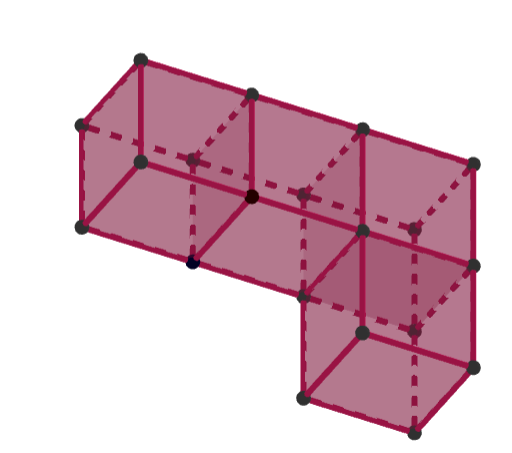
b) Zadání
Pomocí krychlí vytvoř krychlové těleso, jehož portrét je na obrázku.[br]Krychlové těleso postav tak, aby v prvním podlaží byly 3 krychle
Co myslíš, má toto zadání více řešení?
c) Zadání
Pomocí krychlí vytvoř krychlové těleso, jehož portrét je na obrázku.[br]Krychlové těleso postav tak, aby v prvním podlaží byly 4 krychle
d) Zadání
Pomocí krychlí vytvoř krychlové těleso, jehož portrét je na obrázku.[br]Krychlové těleso postav tak, aby v prvním podlaží byla 1 krychle
Co myslíš, má toto zadání více řešení?
[i]Zdroj:[/i][i][br]HEJNÝ, Milan, Pavel ŠALOM, Darina JIROTKOVÁ, et al. Matematika A učebnice pro 2. stupeň ZŠ a víceletá gymnázia. Ilustroval Lukáš URBÁNEK. Praha: H-mat, 2015. ISBN 978-80-905756-0-8.[br][/i][br][br]
Objem - Úkol 1
Rozšířená realita (AR)

V těchto úlohách můžete využít Rozšířenou realitu.[br]U každého zadání, kde to lze, je uveden název apletu, jež máte hledat.[br][br]Nevíte jak na to?[br]Návod najdete v úvodní kapitole této knihy.
Zadání
Níže máme vyobrazená tělesa.[br]Tělesa můžeš natáčet.[br][br]Která tato tělesa podle Tebe mají stejný objem?
Těleso A (Pro Ar pod názvem "HM A 40.4")
Těleso B (Pro AR pod názvem "HM A 39.1b")
Těleso C (Pro AR pod názvem "HM A 39.1c")
Těleso D (Pro AR pod názvem "HM A 39.1d")
Těleso E (Pro AR pod názvem "HM A 39.1e")
Těleso F (Pro AR pod názvem "HM A 39.1f")
Těleso G (Pro AR pod názvem "HM A 39.1g")
Těleso H (Pro AR pod názvem "HM A 39.1h")
Označ tělesa, která mají stejný objem s Tělesem A
Označ tělesa, která mají stejný objem s Tělesem C
[i]Zdroj zadání úlohy: [br][/i]HEJNÝ, Milan, Pavel ŠALOM, Darina JIROTKOVÁ, et al. [i]Matematika B učebnice pro 2.[br]stupeň ZŠ a víceletá gymnázia[/i]. Ilustroval Lukáš URBÁNEK. Praha: H-mat, 2015.[br]ISBN 978-80-905756-1-5.[br]
Sítě I (1. část)
V této kapitole pracujeme s tzv. polyminy, to jsou mnohoúhelníky tvořeny několika shodnými čtverci.
Polyminy
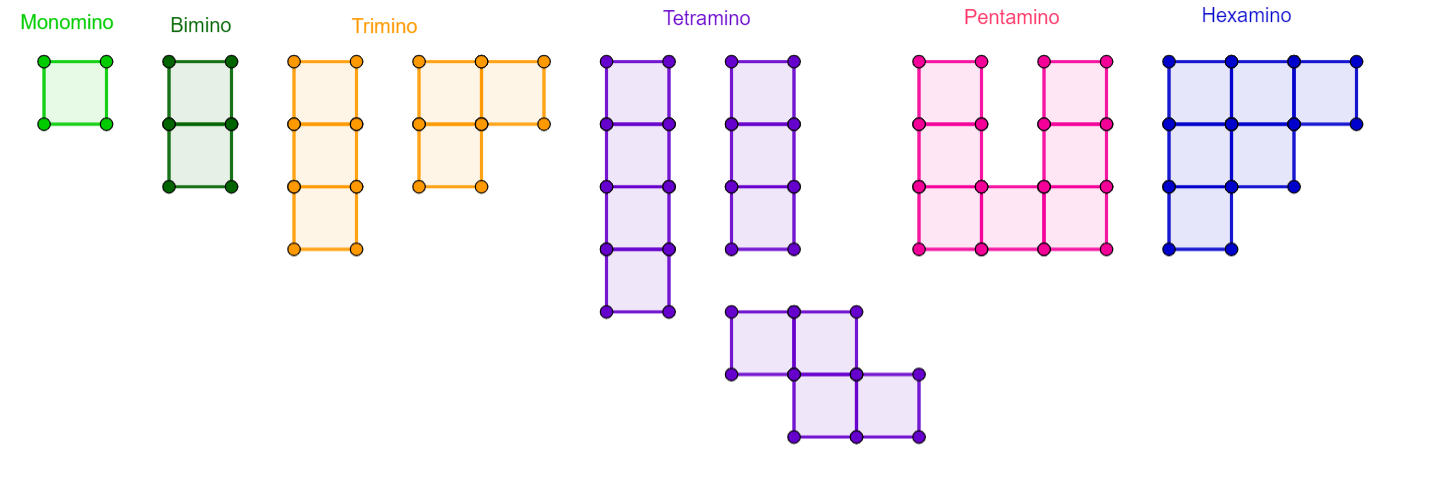
Z pentamina vznikla síť krychle přiložením 1 čtvrece.
Najdi další 3 řešení.
Najdi 4 řešení pro zelené pentamino.
Najdi pentamina, ze kterých přiložením 1 krychle již nelze vytvořit síť krychle.
Najdi tetramino, ze kterého přiložením 2 čtverců nelze vytvořit síť krychle.
Najdi síť krychle, kterou lze vytvořit ze dvou termin.
Najdi síť krychle, kterou lze vytvořit ze dvou trimin.
[i]Zdroj[/i] HEJNÝ,[br]Milan, Pavel ŠALOM, Darina JIROTKOVÁ, et al. [i]Matematika C učebnice pro[br]2. stupeň ZŠ a víceletá gymnázia[/i]. Ilustroval Lukáš URBÁNEK. Praha: H-mat,[br]2016. ISBN 978-80-905756-3-9.
Tělesa
Rozšířená realita (AR)
V těchto úlohách můžete využít Rozšířenou realitu.[br]U každého zadání, kde to lze, je uveden název apletu, jež máte hledat.[br][br]Nevíte jak na to?[br]Návod najdete v úvodní kapitole této knihy.
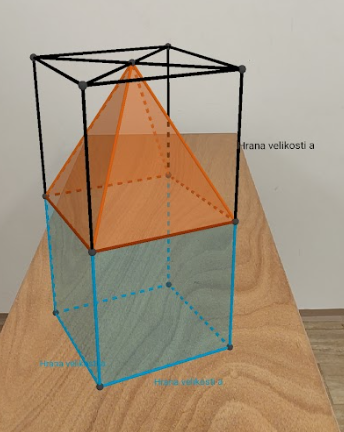
Níže je z těles vyobrazen kostelík.[br]Tělo kostelíku je krychle o hraně délky a.[br]Na těle stojí lešení - stejných rozměrů, jako tělo kostelíku.[br]V lešení je věžička podstavy a * a, výšky a.
Jaký je objem těla tohoto kostelíku?
Jaký je objem věžičky?
(Pro AR hledej aplet pod názvem HM E 24.4)
Kolikrát větší je objem těla než věžičky?
Níže je z těles vyobrazen další kostelík.[br]Tělo kostelíku je hranol o rozměrech a * a * v.[br]Na těle stojí lešení - stejných rozměrů, jako tělo kostelíku.[br]V lešení je věžička podstavy a * a, výšky v.
Jaký je objem těla tohoto kostelíku?
Jaký je objem věžičky?
(Pro AR hledej aplet pod názvem HM E 24.5)
Kolikrát větší je objem těla než věžičky?
Jaký je vzorec pro výpočet objemu jehlanu, když je obsah jeho podstavy S a má výšku v?
Výpočet objemu jehlanu (pro AR hledej aplet pod názvem HM E 24.7)
Jaký je vzorec pro výpočet objemu kuželu, když je poloměr jeho podstavy r a má výšku v?
Výpočet objemu jehlanu (pro AR hledej aplet pod názvem HM E 24.7a)
Zadání
Jaký je objem rotačního kužele o poloměru podstavy r = 4 cm a výšky v = 10 cm?[br]Nejprve odhadni, vypočítej, poté výsledek ověř v apletu výše.
Zadání
Tentokrát mějme kužel o poloměru r = 10 cm a výšky v = 4 cm.[br][br]Odhadni - jaký bude objem tohoto kuželu oproti tomu v předchozím zadání?
Objem vypočítej, poté ověř v apletu výše.
[i]Zdroj[/i]: HEJNÝ, Milan, Pavel ŠALOM. [i]Matematika E učebnice pro 2. stupeň ZŠ a víceletá[br]gymnázia[/i]. Ilustroval Lukáš URBÁNEK. Praha: H-mat, 2017. ISBN 978-80-88247-00-5.
Vztah mezi objemem a povrchem koule
Rozšířená realita (AR)

V této úloze můžete využít Rozšířenou realitu.[br][br]Pro využití AR hledej aplet pod názvem "Hm povrch koule"[br][br]Nevíte jak na to?[br]Návod najdete v úvodní kapitole této knihy.
V knize F je ze stereometrických poznatků věnována kapitola oblým tělesům.[br][br]Kapitola v této knize je věnována vztahu mezi objemem a povrchem koule.[br][br]Pro znázornění těchto vztahů si pomůžeme nádherně zpracovaným apletem Šárky Voráčkové, který je mimo jiné dostupný z odkazu [url=https://www.geogebra.org/m/fafmeqbp]ZDE.[/url][br]
[url=https://cs.wikipedia.org/wiki/Johannes_Kepler]Johannes Keple[/url]r odvodil objem koule rozřezáním na nekonečně mnoho jehlanů. [br][br]Na obrázku je koule nahrazena mnohostěnem, každý poledníkový pás tvoří podstavy 12 jehlanů.[br]Posuň červený bod.
Pro AR hledej aplet pod názvem "HM povrch koule"
Koule na obrázku je nahrazena mnohostěnem sestaveného z celkem 288 jehlanů. Představme si, že ji nahradíme mnohem přesněji, že použijeme milion jehlanů i více - podle toho, jak přesní chceme být. Teoreticky můžeme použít nekonečně mnoho jehlanů. [br][br]Výška jehlanů je rovna poloměru koule [i]r, [/i]objem každého jehlanu je [math]V_j=\frac{1}{3}A_jr[/math], kde [math]A_j[/math] je obsah podstavy. Objem koule [i]V[/i] je součtem objemu všech jehlanů, pro součet obsahů všech podstav dosadíme povrch koule:[br] [center] [math]V=V_1+V_2+...=\frac{1}{3}r\left(A_1+A_2+...\right)=\frac{1}{3}r\cdot4\pi r^2[/math][/center][br][br]Jiný způsob odvození vzorce pro výpočet objemu je pomocí Cavalieriho principu. Sestrojíme válec o poloměru[i] r[/i], výšce [i]r[/i] a rotační kužel o poloměru i výšce r.[br][br][center][img]https://upload.wikimedia.org/wikipedia/commons/8/83/Principio_di_Cavalieri.gif[/img][/center][br][br]
Úlohy k přijmacícm testům
V této kapitole se nachází úlohy na procvičení z oblasti stereometrie.[br]Tyto úlohy slouží ke zopakování a procvičení učiva i k přijímacím zkouškám.[br][br]Úlohy jsou čerpány z knihy:[br]Břicháčková, E. ([2020]). [i]Příprava na přijímací zkoušky na střední školy: vhodné pro žáky 9. ročníku[/i]. Nová škola - Duha.
ZADÁNÍ
na apletu je síť pravidelného čtyřbokého hranolu se čtvercovou podstavou.[br]Obsahy podstavy a jedné stěny je znázorněn v apletu.
Jaký je objem tohoto hranolu?
ZADÁNÍ
Tělesa na obrázku mají shodné podstavy tvaru čtverce a stejně dlouhé výšky.[br]Výšky se rovnají 75% obvodu jejich podstavy.
Součet obsahů [b]všech[/b] podstav těchto těles je 18 cm².
Výška těchto těles je 1O cm.
Objem růžového tělesa je trojnásobkem objemu oranžového tělesa.
ZADÁNÍ
Těleso na obrázku vzniklo tak, že ke kvádru s rozměry 1 dm, 4 cm a 12 cm byl připojen pravidelný čtyřboký hranol, jehož výška je shodná s výškou kvádru (12 cm) a jeho podstava má obsah 9 cm².
Jaký je objem tohoto tělesa?
ZADÁNÍ
Stavba na obrázku je postavena z 5 shodných krychlí.[br]Její povrch je 792 cm².
Jaký je objem této stavby?
ZADÁNÍ
Nádrž má tvar válce s průměrem dna 4 metry a hloubkou 2 metry.[br]Kolik je v nádrži hektolitrů vody, je-li naplněna do dvou pětin?
ZADÁNÍ
V nádrži je .... hektolitrů vody.