IM Geo.5.6 Lesson: Scaling Solids
Find the volume of each cube mentally.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAKsAAACGCAYAAACi2nrxAAAMVUlEQVR4Ae2dW4hNXxzH54VkwighJkPIZRTRyC2mmdSI8KDIyyiPHnjzhuSW3CMSuSYpDaGR2zDkLvdcx708YFzGGGPw+/fdWee/zp69z9nn7L32Xmuf36rd3mvtdfmt7/qctda+rZNH7FgBQxTIM8RONpMVIIaVITBGAYbVmKZiQxlWZsAYBRhWY5qKDWVYmQFjFGBYjWkqNpRhZQaMUYBhNaap2FCGlRkwRgGG1ZimYkMZVmbAGAUYVmOaig1lWJkBYxRgWI1pKjaUYWUGjFGAYSWid+/e0aBBgygvL4+3fxpUVVVpB3HOwwpQ+/btS1OmTKGampqc3k6ePEk9e/ak/Px8mjlzJsOqkwIAtaioiCoqKujChQtWD6uTfWHa8uPHDyotLaV+/fpReXk5VVZWhlm8p7JytmeVQW1ubqbu3bvTpk2bPIkWt0gAdcyYMRao79+/p0mTJjGsujTyq1evEj0qQIX79OkTodFyzdlBRf0ZVk0oAKiYl2HoF6BqYlroZjiByrCG3gzOBQpQy8rKWoFaW1tLb968cU4Yw9CGhoakoV+uIvesshoRHNfV1Vk9KkBtampqZUEuzVkBaklJSWKOaheDYbUrEqIfoHbr1o3cQIUpX758oZ8/f4ZoVTRFpQMVVjGs0bQNeQE1ItNCL1aA2rt3b8JVv5tjWN2UURieCajnzp2j169fK7Qm2qy/fv1qDf0A9e3btymNYVhTyhP8ycePH6cd+uVS4zxnBajDhg0jL6BCE4ZVJkPxMUDt0qVLyjmq3YTv37/Tr1+/7MHG+zMFFRVmWENq9mxADcm00IvJBlSGNaRmEqCOGzfO8fZUKjNOnz5NL1++TBXFqHP19fUZDf1y5bhnldVQcPzgwQNr6AeojY2NGZcQpzkrQC0uLvY8R7WLxbDaFQnQD1A7d+5M2YIKU/CgoKWlJUCroslKgFpYWJj2qt/NQobVTRmf4UGA6tMEbZLLoPqZ0jCsCpr09u3bvntUYVZ1dbX1AEH4Tdt/+PDBGvrRo/oBFfVmWANufYDasWNHX0O/bJLJc1aAOmDAAAoCVIZVpiKg44EDB1KnTp0sWCdMmEB+t/HjxxM2v/lEkX7w4MHUtWvXwEYG7lkDghTZ4EVpfNw3e/ZsWrx4cc5vBQUFlgZBScywBqWkBOuZM2cCy/X48eP0/PnzwPILM6M+ffrQypUrAyuSYQ1Myv971iBhNXnOyrAGCFfQWYlpQJCw/v37N2gzQ8uPYQ1N6swLUgFr5lbok4Jh1actWlmiAtajR4/S06dPW5VlQgDDqnErqYC1R48etHnzZo1r7W4aw+quTeRnVMAaeaV8GMCw+hBPdVKGNVlhhjVZD618KmA9fPgwPXnyRKt6ejWGYfWqVATxVMDaq1cv2rJlSwS18V8kw+pfQ2U5qIBVmbEhZMywhiBytkUwrMnKMazJemjlUwHroUOH6NGjR1rV06sxDKtXpSKIpwJWNPjWrVsjqI3/IhlW/xoqy0EFrMqMDSFjhjUEkbMtgmFNVo5hTdZDK58KWA8cOEAPHz7Uqp5ejWFYvSoVQTwVsPbv35+2bdsWQW38F8mw+tdQWQ4qYFVmbAgZM6whiJxtEQxrsnIMa7IeWvlUwLpv3z7CghkmOoZV41ZTASs+7d6+fbvGtXY3jWF11ybyMypgjbxSPgxgWH2Ipzopw5qsMMOarIdWPhWw7tq1i+7du6dVPb0aw7B6VSqCeCpgHTJkCO3YsSOC2vgvkmH1r6GyHFTAqszYEDJmWD2I/PnzZ5ozZ461wjLWnsK/gVRVVXlI6S8Kw5qsH8OarIejb/78+daCYGI9UIAKaGtqahzjBxWoAlZMAe7cuROUiaHmw7BmKTeWfMTKfm5OgIxe+fz589Ym4sphOHZzKmAdOnQo7dy5061IrcMZ1iybJx2s6HnRIwMOxMUaq/hDMfTKRUVFVhj2mFK4AasC1iyrq0UyhjWLZsB0ADCKaYFTFjgPUAWI2ANYbCIM6QDs+vXrnbJIrM8a5MJsjgUZEsiwZthQAA09JHrNVA6w2qcJ6GHt6SorK1vFE/mq6FnxeiCWfjfRMawZthrgwpbOAVYxbxVxnaYOYkVrEUfeq4B1+PDhhAcDJjqGNYNWA6QAzovTFVYvtusah2H12DJee1SRHcMqlAhuz7B60BKgYp4qbkHJe7fkusKKpYNu3brlZrbW4Qyrh+YBeG6bW3JdYR05ciTt2bPHzWytwxlWjZtHxQWWxtVNaxrDmlai6CIwrMnaM6zJemjlUwHrxo0b6ebNm1rV06sxDKtXpSKIpwLW0aNH0969eyOojf8iGVb/GirLQQWsyowNIWOGNQSRsy2CYU1WjmFN1kMrnwpY161bR9evX9eqnl6NYVi9KhVBvKBhxUs4aPDCwkL6+PGjVaNr164RvssSb4JdvnzZ8n/79s06f/HiRcvf2Nho+fFABPGbm5st/9mzZy3/79+/Lf+pU6csv+UhourqauvtM+E/duwY4f0E4Y4cOUIlJSXCS/iDjlGjRiX8WPx47Nixlh+2z5o1y/oLehFh//79VFZWJrzWPeSJEycm/Hh3t6KiIuHHmgmTJ0+mpqYmKi4uprlz5ybO6XKQp4shmdgRNKx4l7ZDhw60cOFCamhosEx58eIFLVq0iASMdXV1lh+NCffs2TPLL+DEP70gfktLi3Ueq2jD/+fPH8uPFQrhF+7+/fu0ZMkS4aW7d+/S0qVLE368AbZs2bKEH0/XVqxYkfDfuHGDVq1aZfkB67x582j16tWJ81euXKE1a9Yk/PixYfQQ7tKlS7RhwwbhpdraWlq7di0B6Pz8fEL+ujmG9V+LiB5UtwbyYk8Q0wD8CNETt2/fnq5eveql2NDj5CysgBMfO5oMqaDFL6wYHQSomN7o6nIWVgyz+BrB1BeuZaD8wApQMXdFj6ozqKhvzsIqN7bpx9nCahKoOQcrhvzS0tJY9KbyDywbWE0DNedgRYXxrVcchn4/sJoIas7AGoeLKBlO+3EmPaupoOYMrPj02/71rL3BTfZ7hVWA2q5dO+0vppzaIycusPDVatyGfrkxvcCKhxW46geoeLpmoostrBj64z78C+DSwQpQp06dajSoqGtsYc3k83DR6KbuU8EaF1BjDSt61TgP/fIPyw3WOIEaO1hzCdB0sMYN1NjBiiWH8Ag115y9Z40jqLGDFRVKtYJhXCGWYRWgtm3bNqurfoxOYrES3fQy/gIL4srvheomcBj2CFjxojeu+gEqXu7OxOFHPn36dGvpUaxbJtbI1WnebzyseHEaa7vmYo8qYASsy5cvpxkzZmQFKvIBlPalSKdNm0bYdHHGwwoh0bvmsgOs+KQmmx41lW7oCAoKClyjYOlSbOgoMLphQxo4OWz37t2ueWRywkhY6+vrrTW20EAYsnJ9a9OmjaXHiRMnMmn7tHGx8niqpUzRE+MtNjzOxjEeaWOUW7BggTWNQBg2hGHv1xkJKyp98OBBGjFiRM6DCpjKy8sJHxgG6TBa4X8dUi2wLECURzYAi8X35GkZ8sBqk36dsbD6rTinT62Al/kqYLX3vAiz3z7EVAEA+3X+c/BrAafXTgE8qpb/pMTNQDdY7QAzrG4KcrgvBbyCikIYVl9Sc2I/CmQCKsPqR+mA0+ICQacb4gFXr1V24sIIV/LiNpTYYxh3ctyzOqkSYhhu1+DeIuZsuFDAsVtjhWiW8qJwxQ74nDa3+iPcfrfAKQw/fOTr1/EFlqQgbsFgKJRvuwh4pWh8GJECDKsH4Z3+tEMkA9joXQA6ntRg6JSf2OCcPUyk5X1mCjCsafQCjIBVvvEtJ8Gwh5vnuOmNXhnDHZ7YYGkiOQxTCjztYZe9AgxrGu0AoP2+oZwEsAJmee6G5+MIk+dpAnp5iiHnw8fpFWBYU2gEANO90SVglbMRYOKc7FJNJ+R4fOysAMPqrIvVUwLUdLevnGBFlgDT7hhWuyKZ+Vsrmln6WMYWPWo6UFF5hjU8BBhWm9aZgMqw2sRT7GVYJYHFhRE+7xBPb8RevoCSknDPKouh+JhhlQQGkLjyd9rc1srCVMHpboFbmJephWQSH0oKMKySGHyotwIMq97tw9ZJCjCskhh8qLcCDKve7cPWSQowrJIYfKi3Agyr3u3D1kkKMKySGHyotwIMq97tw9ZJCjCskhh8qLcCDKve7cPWSQowrJIYfKi3Agyr3u3D1kkK/AdmvibZo0R4LQAAAABJRU5ErkJggg==[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJwAAACOCAYAAADEpmHdAAANqElEQVR4Ae2dW2wN3xfHKY1bXSO8uScSQV3ioQ1t9YkXRbQhJBURQery4lmppCTu4toHhEQiREhUFKFaFHEJTSMNJUrdqtoqpS37l+/+//dxzu6sc5s505kzayenM2vtPZf9nc/Za80+03O6CS6sgI0KdLPxWHwoVkAwcAyBrQowcLbKzQdj4JgBWxVg4GyVmw/GwDEDtirAwNkqNx+MgWMGbFWAgbNVbj4YA8cM2KoAA2er3HwwRwDX0NAg8vPz+RUjDVpaWhxDuiOAW7RokejWrZvIyMjgl8Ua9OvXT6Smpoq7d+86AjpHALdmzRoxYcIE0bdvX5GTkyOampocIU48nER5eblISUkRSUlJ4siRI13eJccAN3v2bFFZWSnfjSNGjBBXr17tcnHcfgI3b96UkaO4uFisWrVKrq9du1Y0NjZ2WdccBZxSAaIgxG7ZskW5eBmFAq9fvxabN28WWKIcOHBA9O7dW8ycOVNUVFREsUfzmzgSOHTr2LFjUpy5c+eKuro68z3lPUgFSktLxYwZM8SAAQOkxnbL4ljgIMSDBw/EtGnTxODBg8X58+ft1iZuj9fa2ipWrFgho0heXp6or6+3ra+OBg4qtLW1ieXLl0txNm3aZJsw8XAglcNhaVT27t0revbsKdLS0kRZWZlRE8t9jgdO9Rji9OrVS8yaNUu8evVKuXkZRAE9hzNqevv2bTF16lQxaNAgUVRUZNTEUp9rgEOvb926JcVJTEwUJ0+etFQIL++svb1d5Obmyiiyfv168eHDh5jJ4SrgoALm6JYuXSrFWb16dcyE8eKOd+7cKXXFBDwVhs3q4jrgVIcLCwsFRropU6aI58+fKzcv/RQIlcP5NfWt4hOJyZMniyFDhohDhw75/FatuBY4CHDlyhWRnJws35WHDx+2SpO42c+3b9/kSIVlpEVFkXXr1ona2tpINyfbuxo49Ar5xpIlSyR0y5YtIzvKFZErsG/fPqlrZmamKCkpiXwHBlu4HjjVp4KCAtGjRw8xbtw4OX+n/Lw0pwDmQvE599ChQ8X+/fvN7UwIZ/wjND68x2epZgsmhydNmiTflbt37za7O9dvH00OR3VahVhcq5qaGqpZSH/cjHCqp5ijW7x4sYRu4cKFoqOjQ1V5bmkmhzMS6+DBg1JX3MXigYBoStwBp0TYunWrSEhIEMOHD5fzd8rPS3MKPH78WIwfP14MGzZM7Nq1K+KdxS1wUOLcuXNi4sSJ8l25bdu2iMXhDWgF1ETxypUrRXV1Nd1Qq4lr4NDXqqoq+VAnHneaM2eOaG5u1iSIX9PKHM5IpaNHj8o3Mx53unjxolGTTr64B071GP8zAej4FRsN8EQPnkIJVTwDHITAo9bqYxu8+/lljQbqI7FwJpg9BRz+WSc7OzvUm5DrI1Tg2rVrMnLgv+9CFQYulEIuro91DqekYeCUEtrSayOc1fNwmpw+k4HzSRG44jXgAnsfO4uBI7Rl4AhhTLoZOEJArwHHORwBglUf3hO797m9BhzncL5LH7jCwAXq4TaLQypxxbw2whEyWO5m4AhJvQYc53AECBxSCWFMujmHIwRk4AhhXOLmkEpcKK+FVEIGy90MHCGp14DjHI4AgUMqIYxJN+dwhIAMHCGMS9xdGlLxrsI3HeEJ2ydPnoQlGQMXlkyObWQZcOnp6Z2+VTwYRIANX/uUlZUlv+rz+PHjYYnEwIUlU8SNXJXD4bvF8Pw/Ttr/BaiognYjR44MqAagADdYYeCCqRN9natyOPXuiKS7+AJjHa4NGzZ08un7ZOB0RdxlWxJSAZwOTzAZ1LcYqf+KwrbqfxeVD0ujwsAZqeIenyXAIf8aNWqU7+eIcCMQLJxCHqMRzsinS8nA6YpYY6sohWUsiyXAIffCCAVgFDS4IQh28qqdf+eMfP71WGfgdEWssV2Vwxl1GfBg1KOKEVxGPn17Bk5XxF22JSOcUZfVEG1UB58RXEY+fXsGTlfEXXbMgLtw4YIYOHAgqYYRXEY+fQcMnK6INbYaIIKlQVYcyRLgAJf6jSacFNbxBc4AiCpGcMGHMBzshoOBoxQ153dVDgdQ/KczMLIFgw3SGAGHTmMyGDcceBkVBs5IFff4LBnhVHcBTLDRSbULtcQISe2HgQulnrPrLQXOjq4ycLFR2VU5XGwkMN4rA2esi1kvIgqgoyKL2f2r7XmEU0poS6898at1P2YmA0dI6zXgMLLhB/F4hNOA4JCqCWKRyTkcISQDRwhj0s05HCEgA0cI4xI353DEheIcjhDGpJuBIwT0GnCcwxEgcEglhDHp5hyOEJCBI4RxiZtDKnGhvBZSeR6OAIFHOEIYk27O4QgBGThCGJNuzuEIARk4QhiXuDmHIy4U53CEMCbdDBwhoNeA4xyOAIFDKiGMSTfncISADBwhjEvcHFKJC+W1kMrzcAQIPMIRwph0cw5HCMjAEcKYdHMORwjIwBHCuMTNORxxoTiHI4Qx6WbgCAG9BhzncAQIHFIJYUy6OYcjBGTgCGFc4uaQSlwor4VUnocjQOARjhDGpJtzOEJABo4QxiVuDqnEhfJaSCVksNzNwBGSeg04zuEIEDikEsKYdHMORwjIwBHCuMTNIZW4UF4LqYQMlrtdCVxqaqpoaWnxiVFXVxdgv3//Xvz48cNXb2T//PnTV//u3Tuh2wsWLBDZ2dni79+/AvWtra2yvW7/+fNH1v/69UvWh7I7Ojpk+9+/f8v2ut3e3i7r29raZH0oG+1wfmiHots4DupxHBTK/vr1K38/nFRI+7Nx40aRkJAgsFQF33heVFSkTJGUlCT8f3+1T58+4tSpU776xMREcebMGZ/dvXt3cfbsWWnjwuAb2VNSUiRwAAn2pUuXZD1Ahl1cXCztpqYmaZeUlEgbFw71N27ckPanT5+kXVpaKm3Aj/o7d+5I++3bt9K+f/++tGtqaqT96NEjaVdXV0v76dOn0q6qqpJ2ZWWltJ89eybtFy9eSBs/Q4X9v3z5UtoPHz6UtvpZg3v37km7trZW1peVlUn7+vXrAe1kZQz+uG6EwwXNzMyU4uzYsUNKUlFRIT5+/OiTB6LiQqty9+5d8fnzZ2XKi/3ly5cAu76+XtoYwcrLy8W8efMkcBixYOO4KMpuaGiQNgBFPe7yUDDSwG5sbJQ2RhzYABMFIwzs5uZmaQNo2N+/f5c2RlJ/GyMvbDWiK1uN4FiiXo3QaAdbjcjYL2w1AuO4sNUIi/NSdrAfVJYnZ8Ef1wGn+lxYWCihy8nJEeriqzorll7O4fDmwQ+0qFHRCj3VPlwLHDqAMDZ69GgxduxYgY5YWbwOHH4sWY3aVurqauAgBEId4EDeokKsFQJ5GThdP+TDVsHneuCUOFaHWAbuf8oCNPwclf9NmNI8mmXcAIfOI8SOGTPGkhDLwP3DyX9081//1yL8tbgCDt1GiMX8GULs9u3bw1dCa8nAaYL838SvRCK/i7bEHXBKCMAG6ABfNHexDJxSMnCJqRMz0ydxCxxkMhNiGbhA0Iws/E5ufn6+URXpi2vg0OtoQywDRzLjq8CNRG5urs8OZ8WRwGHIxu8++b9CDeN4vAYfcSGMGv30eaQhloELB5/ANrgGoYojgUtPT5e34liqV6hEFbfu+q9Q67fy6CzuYvHCerDCwAVTp3MdtMYbPdRdrGOBQ34QScHIpr/D4NNLuCGWgdOVC22H81GYI4HDaKXDQ3UXoRZPjgAu3LJnZGSIy5cvi/nz50sfbLz0kBwqxDJwlOKh/dCa+izWkcCp0Soc6PCuQjtss2fPHrn+5s0bue6/H6OhHp2nQiwDFxosqgW0plIgRwKHXACwqBfeLaFCrIJLiaAgVDa1xByd0UQxA0cpFrkfUyfqDe9I4PQu4WYAd6DBcoRogVPH0kMsA6eUMbcEaEiR1IDhCuDQ5VAfIJsFDsfwD7FpaWly5DMnN2+tK3D69GkZucL59KfzLZ++txjaycnJQZ9YsAI4nL5/iO3fv79vWkZNz/Dy31RVNFrgcX9cKxVigyHTZcDhrgcnGUlIVduE0zGjTiPERiMobxMcyOnTp4u8vDwjyTv5bAEOyT6mNzDVgWRz+fLlEjbcgQYr+giHtgjDmBLBfrBfLu5SwBbgIAkSTNwo4AXQgo1sSkK01dthdFP70efh1Ha8dK4CtgHnXAn4zOxUgIGzU20+lmDgXAQBUgj1tI2LTjvgVBm4ADnsMfAUBm56/F/6UzD6mSDvxac1uGOO9Hk1fV9daTNwXaC+gkbd/GAZCjjApmb21Sm7ETwGTl09G5eY8I50SkefIsLdO3xuK+47Y7cpbHC+OjwGTXwujGqYw8Q26lVQUOB7Elr5IgXYdwCbVxg4mwXH4QDJiRMnZA6HmwB9rtHolLCNP1RYh89txX1n7DaFDc43KyvL9xEbwivACZXDMXAGQrIrOgUQNgFUsE9OGLjotOWtCAXseFSLOLStbg6ptspNHwzTHv45mt6SRzhdEbbDUgAPH+iPV2EeDsDpfv8d6sCpR7XCueHw309Xr/MIZ/MVUKCo/0bD/3YgnAbL33CKOnDw4eYD2+NxrVA3HTZ3kzwcA0dKE7sKjGQIn3iFAk2dBdoajYBqP0Z1alsnLRk4J10ND5wLA+eBi+ykLjJwTroaHjgXBs4DF9lJXWTgnHQ1PHAu/wHU6viFq7b6XQAAAABJRU5ErkJggg==[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAKAAAACMCAYAAAD7oaJgAAAM00lEQVR4Ae2dWWjVThvGKy4URVywiiguuFAV3Be80aKgvXG9sC6ttbW0aGut1mIVl94IXimIIrhVERG0aF2wirjW3RYrKi6ICioKWkRRcLl4P578vzkmxzk9J9skOXkHwkkmM/POPPM7k5lJMkkhdqyAhwqkeGibTbMCxAAyBJ4qwAB6Kj8bZwCZAU8VYAA9lZ+NM4DMgKcKMICeys/GQw9gVVUV8WbUQOXfItQAjhs3jlJTUykjI4O3jAwaOXIkdenSRSV/4Z0HzMzMpCFDhlBNTY1Swf1qbN68edSvXz9KSVHbJqm15hP1Z8yYQcOGDaPHjx/7JEfeZmP+/PmaHtXV1Qyg21Uxd+7cCHzv3r2jnTt3um3S1+kvXLgwoseVK1cYQDdrKysrKyI27Dx8+JDQGobVLVq0yKAHA+giCdnZ2QaxXTQViKRzcnL+0YMBdKnq8vLy/hHbJVOBSDY3N1eqBwPoQvUVFhZKxYapO3fu0NChQ12w6t8kW/ozMoAO11txcXFM+GCqubmZ6urqHLbq3+Ty8/Nb1IMBdLDuysrKWhTbQVOBSKqgoCCuHgygQ1VZUVERV2yY+vTpE9XW1jpk1b/JtNQN0eeaAdSrYXF//fr1CcGH5O/du0ejRo2yaCkY0YqKihLWgwG0Wad4qIDvcPwVcdmyZab0YAD/amd6j+EzShZvAGYM/d8RAyhTJQE/q/A9ePCApk2bloCFYAUpKSkx1fKJ0jGAQgkTv1bhg4n379/T3r17TVjzf9DS0lJL8KFkDKDJ+rUDn0lTgQhud+qJATRRzU7A9+3bN2poaDBh1b9BV61aZbnlE6ViAIUScX6dgA8m6uvrKS0tLY41/58uLy+3DR9KyQAmUNdOwZeAqUAESXTSPZHCMIBxVGL4jAKtXbvWkZZPpMoACiUkv27A9/TpU8IN+iC6yspKR+GDBgxgDBLcgA+mXr16RZs3b45h1b/eZm43mikFAyhRyy34JKYC4bVhwwbHWz5RcAZQKPH/X7fh+/XrF338+DHKqn8PN23a5Bp8KDUDqKv7OXPmUPv27Wns2LE0efJkVza8iN2mTRtX0nY6z3hnd+DAga6+SsoA6gCcOHEiTZo0SeujoZ/mxobL2Zo1a1xJ2+n8pqen0/Lly3UKOb/LAOo0BYC7d+/W+YR7d/bs2a4PmBhAHWMqAMQoGP2qIDgGUHEtqQAQ84BLly5VXDJr5hhAa7pZjqUCQMuZ8yAiA6hYdAbQKDgDaNTD9SMVAOJpmG7durleFicMMIBOqGgiDRUA4nnAxsZGE7nyLigDqFh7FQAqLpItcwygLfnMR1YBIN4J2bNnj/nMeRCDAVQsugoAm5qaaPr06YpLZs0cA2hNN8uxVABoOXMeRGQAFYvOABoFZwCNerh+pAJArA2DJ2KC4BhAxbWkAkCsjnXq1CnFJbNmjgG0ppvlWCoAtJw5DyIygIpFVwHg58+f6dy5c4pLZs0cA2hNN8uxVACINaKxnFsQHAOouJZUAKi4SLbMMYC25DMfmQE0asYAGvVw/UgFgEH6UhID6DpyRgMqAMS34nbt2mU07NMjBlBxxagAUHGRbJljAG3JZz6yCgC/f/9Ojx49Mp85D2IwgIpFVwHgtWvXqFOnTopLZs0cA2hNN8uxVABoOXMeRGQAFYvOABoFZwCNerh+pALAZ8+eET7mEgTHACquJRUAvnz5ktatW6e4ZNbMhRLA7du3a0t2WZPMXiwVANrLodrYoQLwy5cv2oOaffv2dX1BnFjVqALAP3/+EMoaBBcqAEeMGEHV1dXaunmJLmGLlZWuXr0aqdDXr19r+6hg+OOzWMJhXx9W+Ot/VQDI0zB6xX24QCUWWYwHIMDr3LlzZJHH3NxcrVSIt2TJEgLMSAfzbStXrqRZs2ZFwsIPoMqcCgB//vxJb9++lZn3nV+oWkChfjwA0boBPkAY7QAgLuHiEgfQUlJSCP1K4QBrLMBVACjyEYRfBlBSSwAPLZzMAaxouACgvsWThRFpqQDwzZs3tGXLFmHS178MoKR6ACBaSZmTwQUA9U4WRpxXAeCTJ08oJydHmPT1LwMoqR4AGOu1RhlcfgNQUiTfejGAkqpB/w79PIyYhRN9PgZQKOLMLwMYQ0dMqQBCtITYMMqFCwKAN27coF69esUomb+8QwmgmSrA4EI/wDATVxZWRR/w69evdPv2bZl53/kxgIqrRAWAiotkyxwDaEs+85FVAPjhwwc6dOiQ+cx5EIMBVCy6CgCPHj1KPXv2pB07dmilA5CjR48mLN0Lt3Xr1sg84Y8fP7RzeJEJDi8z4Xu9wo0fP57w2Qe4w4cPGx7zmjp1Kt29e1c7h7VosrOzRTTCJ8kuXryoHV++fJlmzpwZOYeJ+hMnTmjHGRkZhM91CVdSUkIHDx7UDl+8eEFjxowRpwhf0zRTJizUCYd8Rc9URBJ1acc4MeeSESvJqgAQtwYB0f3797Us4h2Rffv2ET5iCHfr1i3CQAXu9+/f2jkBZ0NDAwEY4Q4cOEBY6gMO75nU1dWJU3TkyBESlfz8+XPDgkjHjx+P9J0xMX7s2LFIvNOnTxOeWYTLzMzUYBUnz58/T3itFK65uZn2798vTml3psyWqaamhlq1akVFRUWRdFTshBpAFQI7ZcPNSzBa2datW9PGjRudym7C6YQOQIzUcSkT85UJK+VxQLcAPHnyJLVt25bw4UYvXOgAhMgQPWjODQDRH23Xrp3WZ/RKj9AAiAlz/TOJXglu1a7TAJ45c4ZSU1OpsrLSapYciRcaADHgwBZU5ySAZ8+e1T4Grh/Fe6VLaAD0SmCn7DoFIBbk7NChA1VUVDiVNVvpJDWAYsDh5C1CW2rbiOwEgJi66dixI5WXl9vIibNRkxpASKV/UsdZ6dSmZhfACxcuaK9FrF69Wm3G41hLSgAx2EiGVk9fd3YAxJ0WvDpRVlamT9IX+0kJIAYbeBwsmZxVAC9dukRdu3al0tJSX8qRlAD6UmmbmbICIG4V4nvIK1assGndvehJAyAuubhhH7Q7HIlWrVkA8d519+7dqbi4OFETnoRLGgChXrIMOGQkmAHw+vXr1KNHD8MTObI0/eAXeAAx4EjWVk8PSKIA1tfXa4+YqX6qRZ9XM/uBBzAZBxyyCkwEwJs3b2rvuBQWFsqS8KVf4AH0paouZCoegHh2sXfv3lRQUOCCdfeSDCSAyT7gkFV3SwDik2N9+vSh/Px8WVRf+wUSQCiazAMOGTGxAMQ3j/F8Y15enixai354LA0T1F7OmQYKwLAMOGTUyADEY/f9+/cnsSKZLF4sP0CHdX3wHjcDKFFJ9k5IWAYcEjkoGsDGxkYaMGAALV68WBY8rh+uIJg9iLcCmkgIq5phnhWbWOEMaWB5FgAMf+QRjQT8sA+/qqoqkYT0N1AtoLQEIfHUA4hKHjRokOHtOqsyJAIgWliEA1higz2Ah0u4WMoZDQS6A/qw0Uu3ROfT9wCGccARXUk4FgA2NTXR4MGDaeHChbJgpv3iAQjY8aqmbK4VAEZf/hEWkAqHMAAzlvM9gMh42AYcssoCgPikRHp6Oi1YsEAWxJJfPAABE8LIHODCpnfR7xXjfKz4iOdbAIcPH07btm3Tly3U+1OmTKG0tDTKyspyVAcGMIacePMf/ybe/mowYcKEGGpZ944HILpAqINYl+CkbQGtS8oxzSgQD0CkhT4clt6rra3VNjEKTupLsBkROax1BcRUSrwUEA4DDmzivWr9iFjEj24REaalPrxv+4CiQPyb3AowgMldv74vXSgBRMcaGzvvFQgdgOiPeH0D3vtq908OQgUgOsi4AR/me8r+Qe+/nIQKQHGLSDZ9EF0xmPfCe7SYfkCLKW4noQXFhmP44zyOMTIUYfGNPNm8WbQNPvbxnRA3KycRADHdgEeV0FcETLgnCoe4AE9MReAXH13EfJoI6/UjTm5q53TaoWoBhXjxAARwLc3+Aza9Q1gBJPzRIkaH0Yfn/b8KMIB/tYjs4VKNVk3mAG+8J0AQnwGUqfevHwP4ryba5RatmszJWk+EFf1LxGEAZcrJ/eQqy8Mmja8MoujCoQXUQyXOy+IygEId878MYAzN0I8DhHikHBvAg2MAYwhm0TuUAKJlk7Vu0Rpi5CuAE+FlcRFGf2cF+wCYXXwFQglgfFk4hCoFGEBVSrMdqQIMoFQW9lSlAAOoSmm2I1WAAZTKwp6qFGAAVSnNdqQKMIBSWdhTlQIMoCql2Y5UAQZQKgt7qlKAAVSlNNuRKsAASmVhT1UKMICqlGY7UgUYQKks7KlKAQZQldJsR6oAAyiVhT1VKcAAqlKa7UgVYAClsrCnKgUYQFVKsx2pAgygVBb2VKUAA6hKabYjVYABlMrCnqoU+B/6gOT+57PQegAAAABJRU5ErkJggg==[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAK0AAACVCAYAAAAqhnqDAAANDElEQVR4Ae2df2hN/x/HV0pCLWnSkh8tRYtJyNKaECEx2t8TkSyMUEiUIiFJWSH8QX5EfmVW8nNGyM/W/JgNmd8/59dazOvb8+x77ufueN27c+59nbt77vv1rrN7z/t9zuuc8ziP+977/HqfNNKkBAJGIC1g66urqwRIpVUJAkdApQ3cLtMVVmnVgcARUGkDt8t0hVVadSBwBFTawO0yXWGVVh0IHAGVNnC7TFfYGGmrq6spIyOD0tLSdBBmUFRUlNBfkhHSPn78mAYNGkTZ2dlUVVWVUMCpvLDCwkKrAsjPz0/oZqa8tDU1NZSTk6PCCmsFYTt06ECrV6+m0aNHC0ePHi6lpa2traWhQ4eGhF2zZg1t3rw5OhEtbZMAhO3YsSM1NjbS2rVrVdo2ibmc4NmzZzRs2LCQsJitoqKCbty44TKCTsYRgLCdOnWiHz9+WMUqLUcphrwXL17QiBEjWgkbQxidxUEAwnbu3JkaGhpCJSptCEXsX+rr6yk3N5cV9uHDh4Q2ribvBCBs165d6dOnT61mVmlb4fA+8vr1axo1ahQrLKIVFxfTypUrvQc2fA4Im56eTu/fv/+HhEr7DxL3GW/fvqW8vLyIwrqPpFOGE4Cw3bp1ozdv3oRnh76rtCEU3r6gBsC5Qj0P641bW1ND2O7duxOaXJGSShuJTJT8jx8/0pgxY1wJu23bNtq9e3eUaFpkE4CwPXr0IBzURksqbTQ6TNnnz59p3LhxroTF7CdPnqTy8nImkmaFE4CwPXv2pLq6uvBs9rtKy2LhM79+/Urjx493LSwfRXOdBCBsZmYmPXnyxFnEjqu0LJZ/M79//04TJ070LCzavmhOaOIJQNhevXoRTg26TSqtC1I/f/6kyZMnexYWoWfOnEklJSUulmLeJBC2T58+nm8oUmnbcAXXuqdMmRKTsAiN+TFoak0Awvbr14/u37/fusDFmEobBVJTUxNNnTo1ZmGjhDa6CMJmZWXRnTt3YuKg0kbA9vv3byooKIhb2P3799OxY8ciLMW8bAjbv39/un37dswbr9Iy6Jqbm2nGjBlxC4vQe/bsoUOHDjFLMS8Lwg4YMIDu3r0b18artAy+6dOnU5cuXWj48OHWfZu44ViH+BgMHDjQOkvw4MEDhri3LJWW4QVBcaML4MQ74CZwDPHGCfr8YDp//nyGtvcssEC8RKakf3IBQABGIukprxaKkkxVWsZMScC48SPS3UrMolM2S5KpSstoIgmYCW9kliRTlZZRSBJwWVkZXbhwgVmKWVmSTFVaxh1JwJs2baLS0lJmKWZlSTJVaRl3JAEz4Y3MkmSq0jIKSQJmwhuZJclUpWUUkgSMO7xwntb0JMlUpWVskgSMu5jQEZ3pSZKpSsvYJAmYCW9kliRTlZZRSBIwukSK9RY8ZtUCmyXJVKVlNJAEvGLFClq/fj2zFLOyJJmqtIw7koCZ8EZmSTJVaRmFJAEz4Y3MkmSq0jIKSQJet24dbd26lVmKWVmSTFVaxh1JwBcvXqTKykpmKWZlSTJVaRl3JAEz4Y3MkmSq0jIKSQJ++vQpoYdw05MkU5WWsUkS8Ny5c2n58uXMUszKkmSq0jLuSAJmwhuZJclUpWUUkgTMhDcyS5KpSssoJAl4x44dtG/fPmYpZmVJMlVpGXckAR89epTOnDnDLMWsLEmmKi3jjiRgJryRWZJMVVpGIUnA6DkcnTGbniSZqrSMTZKAtbOOFsCSTFVan6X99u1b6PWYzKKMyVJpfd7VkoB9XtXAhJdkqjUts9slAaObT7zhxvQkyVSlZWySBLxz505Cx8qmJ0mmKi1jkyRgJryRWZJMVVpGIUnATHgjsySZqrSMQpKAZ82aRUuWLGGWYlaWJNPASfvlyxfr3Vzx9tsfTRlJwM+fP6eXL19GW5wRZZJMAyftokWLqKioiPAYi19JErBf6xi0uJJMAyctdhb6xmpLWkwTa20sCfjcuXN0+fLloDkmvr6STFNa2uPHj8cEXxLwhg0baPv27TGtRyrNJMk0ZaWNZ4dLAo5nPVJpXkmmKSttfn5+qAmBpgTawXhlKF4gjAEQcVDHJUnAXHwT8ySZBlJaSNjWE65OadPS0ii8uYDySJ1oSAJetmwZocMO05Mk00BK60YAp7Q5OTmtZsOBGmpeLkkCxjtgJd5SyK1nkPIkmQZKWvQ+6BxqamrYfeeUFuPhCdI68+xyScB2TNM/JZkGSlq8RI4bOCGSRVqtaVv2jrHSYvPRlr106ZLnNq2zVk1UTattWsOlhbCQzT4bEO0CQ7LUtNx/ARPzjK5p7R0OYSFwpISrYfYpLXw6r47hB+DMs2NJArZjmv4pyTRQbdrwHY8j/7ZOe4VP7+W7JGC9ItZCXpJpIKXdu3cvYfArSQLGvQdXrlzxa1UDE1eSaeCk9VtYWCAJODBW+byikkwDJS2uaA0ZMoSw0hj8qm0lAev9tC2/BkmmgZIWbVgcgNlDpAOpeCsNScD65ILh0sYro9v5JaV1u8xUn06SaaBq2kTtWEnAiVrnZF+OJFOVltnbkoC134MWwJJMVVqfpdUeZlRaRjH5LMlaQX7tghlRkqnWtIwDkoC118QWwJJMVVqfpdX+aVVaRjH5LMlaQXsCV2nlDWUiSkrLhDcyS5KpNg8YhSQB69ttWgBLMlVpfZZW3yOm0jKKyWdJ1gryaxfMiJJMtaZlHJAEzIQ3MkuSqUrLKCQJeM6cOTRp0iRqaGiwlnTv3r1QzzfIQNf2Hz58sMqqq6upvLw8tEZHjhyhV69eWeO1tbV06tSpUNmJEyeorq7OGkdXomg72+ns2bP06NEja/Tdu3d04MABu4jOnz8f6ocBjyHhFah///61yisqKujWrVvW91+/fllljY2N1vjNmzepsrLS+v7nzx+rzMs22UyxTfX19VacWLdp4cKFlJeXZ8VI1J+0RC0o1uXYgGOd354PUmRmZlJWVhbhvlqk0tJSWrx4sT0JDR8+PCQR5Jo9e3aobOzYsXT16lVr/PTp01RYWBgqKygooLKyMmscvTJOmDAhVIYuoA4fPmyN4/bN3NzcUNmCBQto165d1jikGTx4MEFCpFWrVtGWLVus7/ghoQyn7JA2btwYeiavqanJKvOyTTbTeLYJl8Srqqqod+/eVh/F1ool6I8x0oJntCeGE8Q7KRZjSxvPykDY7OzsVj/eeOJ5mTflpUXt5tcN6l5AJ9O08UrbnsKCY8pLi8eA0GO5pv8IxCNtewtrhLT/7Sr9ZhOIVdpkEDZlpcVBF/q99asvBnvnB/UzFmmTRdiUlRYbpgddkX9SXqVNJmFTTlo96IosaniJF2mTTdiUk1YPusLVjPzdrbTJKGzKSRt5N2lJOAE30iarsCkhrR50hevo7ntb0iazsCkhLTZCD7rcyWpPFU3aZBc20NLqQZetoPfPSNIGQdhAS4tOnPVKl3dhMQcnbVCEDbS0se0unYuTNkjCBk5aXOHq27evXumK87cXXtPGIyyOJXDlMdEpcDfM+NUPbqLBt+fybGnjERZnbdA8i/auDb+2MRDSzps3T28vFDQA0hYXF4vcD+tGWryTQ/L20EBIO3LkSD3oEpQWT2hkZGSI3MDtRlq891jy5qWklxYPzuEF0DrIMsBTBxLJjbSoZdGcQIK8GDCOFydi8JqSXlqvG6TTJ5aAG2nDX36I6adNm2YdwKHZgJd74+DaltrN2qu0bijpNBEJuLka6ZQ2PT29laQQ18sBtkobcXdoQSQCzc3NhKeAuYGbxyktxsMTal83NbY9j0prk9BP1wQg7dKlS/8Z7L4XnIGc0joFVWmdxATH7YMIwZBGhFJp22k3o80F+M5aop1WJykWCyY4u9NWu1albafdhVoWO6ctaXEU7OVIuJ02J+7FgoUta1sXD1TauHHHHsCNtOgGqS2xY1+D5JwT22sLnIg11AMxD5TdSGtKTWtjw/aipk1kUmk90HYjLaaxax00KdDuwxWhkpISq6M29IyYKgnC4l+/5H0FbtiotG4o/X8aN9LiX6XdPMD0uNqDHYu3tmPAiXS73MOik27S9hIWIFRaYR2c0uKeCdS4drLPQtjjQf3EduIHiTvGMGC7EpVUWhekr127Rs7h+vXr7JyctOETovZFzaspdgIqrQt2Bw8eJOeg0roA59MkKq0wWK1phYEy4VRaBoozCwcdeLQE52DxGd5GdU6r0jqJyI+rtC6Z2qLi9A7EjJRwQGIflGBaZ/sVefroeyR67vJVWnecQlPhtBUeH9HUfgRUWg/s0UxAEwGfmtqPgErrkr0K6xJUAiZTaV1AVmFdQErgJCqtC9g4CLPPCtifLmbTSXwioNL6BFbD+kdApfWPrUb2iYBK6xNYDesfAZXWP7Ya2ScCKq1PYDWsfwRUWv/YamSfCKi0PoHVsP4RUGn9Y6uRfSKg0voEVsP6R0Cl9Y+tRvaJgErrE1gN6x+B/wF0brvb/t4wdgAAAABJRU5ErkJggg==[/img]
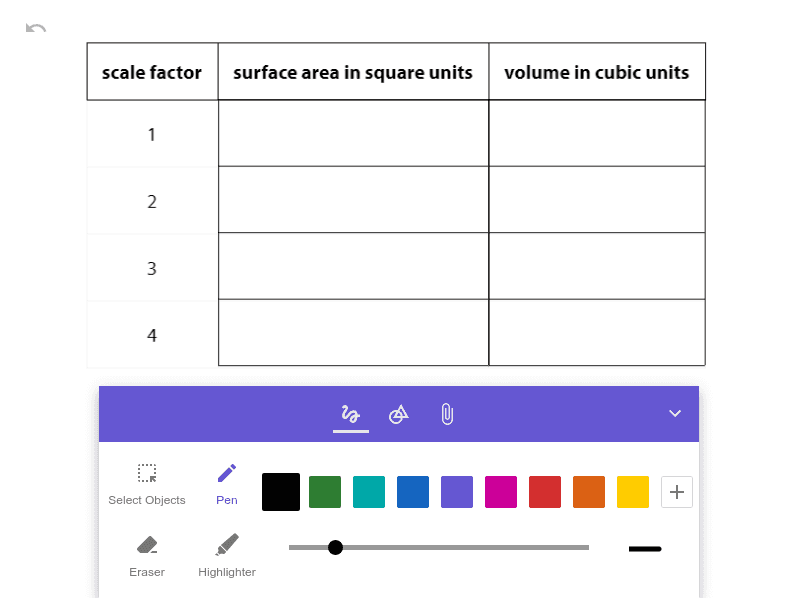
Use the applet to build cubes that result from dilating a unit cube by each scale factor shown in the table. Then, complete the table with the surface area and volume of each dilated cube.
Suppose a unit cube is dilated by some scale factor k.
Write an expression for the surface area of the dilated cube.[br]
Write an expression for the volume of the dilated cube.[br]
Compare and contrast the expression for surface area and the expression for volume.[br]
[size=150]Clare says, “We know that if we dilate a cube by a factor of [math]k[/math], the cube’s volume is multiplied by [math]k^3[/math]. It seems like that must apply to [i]all[/i] solids, but I’m not sure how to prove it.”[br][br]Elena says, “Earlier in the unit, we showed that we can cover any two-dimensional shape with rectangles, so the property that area changes by [math]k^2[/math] when we dilate a figure by [math]k[/math] applies to all shapes, not just rectangles. Can we do something similar here?”[/size][br][br]Use Elena’s line of reasoning to argue that for [i]any[/i] solid, if it’s dilated by a factor of [math]k[/math], the volume is multiplied by [math]k^3[/math].
Suppose a triangular prism has surface area 84 square centimeters and volume 36 cubic centimeters. The prism is dilated by scale factor [math]k=4[/math]. Calculate the surface area and volume of the dilated prism.
The image shows a figure called Sierpinski’s triangle.
[size=150]It’s formed by starting with an equilateral triangle, then repeatedly removing equilateral triangles created by joining the midpoints of the existing triangle’s sides. The first few stages are shown.[br][br][/size][table][tr][td]stage 1[/td][td]stage 2[/td][td]stage 3[/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALYAAACaCAYAAAAEnrJJAAAMV0lEQVR4Ae3bCUgUbRgH8Myk08KirExKTMTCwkLsvgu77wO7TCyspKLESkpMKqLors+k+5TuUyyspMREKkws7DIsurSosLKD8v14wmR2cndnZ2d23pn5B0NzvDPzvP/3t49RbS2GX0jAgAnUMuCcMCUkwAAbCAyZAGC7YFlLS0td8Ba8QpgAYAvTUGE/OzubxcTEqPBkPNJWAoBtKx0Frg0aNIjVqlWL5eTkKPA0PEJqAoAtNSkZ4w4ePPgHNcEeMmSIjCfgFrkJALbc5OzcV1lZyfz8/KphE+7Dhw/buQuXlUoAsJVKUvScxMREC9QE29/fXzQKh2olANgqJPv06dN/UBNs2pKSklR4Ix4pTgCwxYkocDxt2jSrsN3c3FhxcbECb8EjbCUA2LbSkXHtypUrVlH/7dozZsyQ8WTc4kgCgO1IWhLG9ujRwy5sAp6ZmSnhaRgiNwHAlptcDfelpKRIQk2we/bsWcMTcEqpBABboSS/fPnCvL29JcMm3KmpqQq9HY8RJwDY4kRkHsfFxTmEmmC3atWKVVRUyHwjbrOVAGDbSkfitYKCAodRE2za4uPjJb4FwxxJALAdScvK2HHjxsmGTbgLCwutPBmn5SYA2HKTq7rv7NmzTqEm2BMmTHCyCtwuTgCwxYk4eNy5c2enYRPu8+fPO/hmDLeVAGDbSsfOtY0bNyqCmmCHhITYeRsuO5IAYDuSlmBsWVkZ8/T0VAw24d60aZPgDdh1JgHAlpnevHnzFEVNsJs0acLev38vsyLcJkwAsIVpSNzPzc1VHDXBpi02NlZiFRhmKwHAtpWOlWvh4eGqwSbceXl5Vt6M01ITAGypSVWNO3r0qKqoCfawYcMcrArDxQkAtjgRO8cBAQGqwybcaWlpdirBZVsJALatdETXkpOTXYKaYAcGBorejkNHEgBsiWmVlJQwd3d3l8Em3KtXr5ZYHYaJEwBscSJWjiMjI12KmmB7eHiwFy9eWKkIp20lANi20qm6du3aNZejJti0RUVFSagQQ8QJALY4kRqOe/furRlswp2VlVVDVThlKwHAtpUOY2z37t2aoibYffv2tVMlLosTAGxxIoLj79+/Mx8fH81hE+69e/cKKsOuvQQA20ZCy5Yt4wI1wfb19WU/f/60US0uCRMAbGEagv0HDx5wg5pg05aQkCCoELu2EgBsK+lMmjSJO9iEu6ioyErFOC1MALCFaVTtX7x4kUvUBHvKlCk1VIxT4gQAW5wIY6xr167cwibc6enpNVSNU8IEAFuYBmNsy5YtXKMm2KGhoaKqcShOALAFiXz48IF5eXlxD5twb9++XVA5dsUJALYgkQULFugCNcFu1qwZ+/Tpk6B67AoTAOyqNG7fvq0b1ASbtkWLFgnXEvuCBAC7Kozhw4frDjbhvnv3rmA5sfs3AcBmjB0/flyXqAn2qFGj/q4lfhckANiMsaCgIN3CJtwnT54ULCl2KQHTw167dq2uURPsjh07QrMoAVPDfvnyJatbt67uYRPudevWiZbW3Iemhh0dHW0I1AS7fv367PXr1+bWLJi9aWHfuHHDMKgJNm1z5swRLK25d00Lu3///oaDTbizs7PNLbpq9qaEvW/fPkOiJtiDBg0CbDP+rcivX79Y27ZtDQubcB88eND0uE3XsVesWGFo1ATbz8+PVVZWmhq3qWA/evTI8KgJNm2JiYmAbZYEIiIiTAObcD958sQsS/vPPE3TsTMyMkyFmmBPmzbtnwU3ywnTwA4LCzMdbMJ95coVs1i2mKcpYO/YscOUqAl29+7dLRbcLAeGh11eXs6aN29uWtiEOyUlxSyeq+dpeNiLFy82NWqC7e3tzb58+VK96GbYMTTs/Px806Mm2LTFxcWZwXP1HA0Ne/To0YBdBZtwFxQUVC+80XcMC/vUqVNALUBNsMeNG2d0z9XzMyzs4OBgwBbBJtxnz56tXnwj7xgS9vr164G6BtQEu3Pnzkb2XD03w8F+8+YNa9CgAWBbgU24N27cWA3AqDuGgx0TEwPUNlATbE9PT1ZWVmZU03/mZSjYOTk5QG0HNcGmbd68eYCtlwQGDx4M2BJhE+7c3Fy9LK3DdRqmYx86dAioHUBNsMPDwx0Go5cbDAPb398fsB2ETbiPHj2qF6sO1WkI2ElJSUAtAzXBDggIcAiMXgbrHnZxcTFQy0RNsGlLTk7Wi1fJdeoe9vTp0wHbSdju7u6spKREMho9DNQ17MzMTKB2EvXfrh0ZGakHr5Jr1DXsnj17ArZCsAn4tWvXJMPhfaBuYe/atQuoFURNsPv06cO7V8n16RL2169fWcuWLQFbYdiEe/fu3ZLx8DxQl7Dj4+OBWgXUBNvHx4d9//6dZ7OSatMd7MLCQqBWCTXBpm3ZsmWS8PA8SHewx48fD9gqwybcDx484Nmt3dp0BfvcuXNA7QLUBHvSpEl28fA8QFewQ0JCANtFsAn3xYsXebZrszbdwN60aRNQuxA1we7atatNPDxf1AXsd+/escaNGwO2i2ET7q1bt/Ls12ptuoA9f/58oNYANcH28vJiHz58sAqI1wvcw87LywNqjVATbNoWLFjAq1+rdXEPe+jQoYCtMWzCffv2bauIeLzANexjx44BNQeoCfaIESN49Gu1Jq5hBwYGAjYnsAn38ePHrULi7QK3sFevXg3UHKEm2EFBQbz5tVoPl7CfP3/O6tSpA9icwSbca9eutYqJpwtcwp41axZQc4iaYNetW5e9fPmSJ8M11sId7OvXrwM1p6gJNm3R0dE1YuLpJHew+/btC9icwybcN27c4MnxP7VwBXvPnj1ArQPUBHvAgAH/YOLpBDewf/z4wdq0aQPYOoFNuPfv38+TZYtauIG9fPlyoNYRaoLdtm1b9uvXLwtQvBxwAbuoqAiodYaaYNO2YsUKXixb1MEF7MmTJwO2TmET7sePH1ug4uFAc9iXLl0Cah2jJtgRERE8WLaoQXPYoaGhgK1z2IQ7IyPDApbWB5rC3rZtG1AbADXBDgsL09qyxfs1g/3x40fWtGlTwDYIbMK9c+dOC1xaHmgGe+HChUBtINQEu3nz5qy8vFxLz9Xv1gT2nTt3gNpgqAk2bYsXL67GpeWOJrBHjhwJ2AaFTbjz8/O1NP3n3S6HfeLECaA2MGqCPWbMGPPB7tChA2AbHDbhPn36tKa4Xdqx161bB9QmQE2wg4ODzQH71atXrF69eoBtEtiEe8OGDZrhdlnHnj17NlCbCDXBbtiwIXv79q0muF0C++bNm0BtMtQEm7aYmBjjwh44cCBgmxQ24c7JyXE5btU79oEDB4DaxKgJ9pAhQ4wF+/fv36xdu3aAbXLYhPvw4cMuxa1qx165ciVQA/UfA/7+/saATd+qoE8qNmTw10BSUpLLcKvWsadOnQrU+GBbGHBzc2PPnj1zCW5VYF++fNliQn8/sfgd3XvGjBn6hd2tWzfARre2aiAzM1N13Ip37P/++8/qhNCx0bHJQK9evfQF+/Pnz6xFixaAjW5t10BqaqqquBXt2EuWLLE7IXRtdG0y0KpVK1ZRUaEabsVg37t3D6jRqR0yEB8fzz/ssWPHOjQpdG50bjJQWFioCm5FOvaZM2eAGt1aloEJEybwC7tTp06yJoWuja5NBs6fP684bqc7Nn1LAkAB1BkDISEhfMEuLS1ljRo1Amz8McRpA5s3b1YUt1Mde+7cuU5PyJlPOu41zk+KJk2asPfv3yuGWzbsW7duATU6taIGYmNjtYdN34pAxzROx+RlLfPy8hTBLatjHzlyBKjRrVUxMGzYMO1gt2/fXpVJ8dI1UIe2P4nS0tKcxu1wx161ahVQo1uraiAwMNC1sOnbD7Vr11Z1UuiW2nZLXvJfs2aNU7gd6tgzZ84EanRrlxjw8PBgL168kI1bMuyrV6+6ZEK8dAzUof1PjqioKPVh07cesNjaL7bZ1iArK0sWbkkdm77tYLZAMV8+PsT9+vVTB/a3b99Y69atARt/ttbMwN69ex3GbbdjL126VLMJoWvy0TW1XgdfX1/28+dPh3DbhH3//n2gRqfmwkBCQoJysCdOnMjFpLTuGHg/Hz85Hj58KBm31Y594cIFoEa35srAlClTnIfdpUsXriaFrslH19R6HdLT0yXhrrFj0z+d038fxIYMeDQgRXaNsKXciDFIgOcEAJvn1UFtshMAbNnR4UaeEwBsnlcHtclOALBlR4cbeU7gf7QQmfY2gwMEAAAAAElFTkSuQmCC[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALQAAACaCAYAAAAAa2J0AAAPNklEQVR4Ae2cCWwVRRjHS4RUAWmpCEQNoBFplCCItkYMFI+CHBI15YgWFIMg0oooIERqo1DvotBCwAgKrY0YFFQ0Ujy4VGhpqHKFK0rqRYF6IRAqYz7DPreP3bczO7M7Mzufycvum53jm//368vz8Z8vieB/qECEFEiK0F5wK6gAQaADgODgwYMBzIpT0iiAQNOoxNgnJyeH7Nmzh3EUdhehAAItQkXbHB988AFJSkoio0aNsrXibVgKINCCle7du/d/QAPUn3zyieDZcTovBRBoL4UYnr/22msxmAHozMxMhtHYVYQCCLQIFQkhDQ0NJC0trQnQAHVpaamgFXAaGgUQaBqVKPpMnjz5HJgB6Pbt25M///yTYgbsIkIBBFqAijU1NY4wA9DweuKJJwSsglPQKIBA06jk0WfYsGEJgQaov/32W49Z8LEIBRBoThVXrlzpCTMAfc8993CuhMNpFECgaVRK0KdHjx5UQAPUq1evTjATPhKhAALNoeJLL71EDTMAfd1113GshkNpFECgaVRy6PPrr7+S1q1bMwENUL/66qsOs2GTKAUQaJ9KTpw4kRlmADo1NZUcPXrU56o4zEsBBNpLIYfn33zzjS+YAWh45efnO8yKTSIUQKB9qHjHHXdwAQ1QV1dX+1gZh3gpgEB7KRT3vKKightmAHro0KFxM+NbEQog0IwqpqenCwEaoH733XcZV8fuXgog0F4K2Z4XFRUJgxmA7t69u212vBWhAAJNqWJdXR1JTk4WCjRA/eKLL1JGgN1oFECgaVQihIwbN044zAB0q1atyC+//EIZBXbzUgCB9lKIELJhw4ZAYAag4fXwww9TRIFdaBRAoClUuvXWWwMFGqD++uuvKSLBLl4KINAeCr311luBwwxADxgwwCMSfEyjAALtodIVV1wRCtAAdXl5uUc0+NhLAQQ6gUKFhYWhwQxAX3XVVQmiwUc0CiDQLipB9aNmzZqFCjRAPXv2bJeIsJlGAQTaRaUxY8aEDjMA3aJFC3Lo0CGXqLDZSwEE2kGhzz77TArMADS8HnzwQYeosIlGAQTaQaW+fftKBRqgXr9+vUNk2OSlAAIdp9Drr78uHWYA+pZbbomLDN/SKIBA21Q6deoUueyyy5QAGqB+8803bdHhLY0CCLRNpZkzZyoDMwDdpUsXcubMGVuEeOulAAJ9ViGo5wwQqfYqKCjwyiE+tymAQJ8VA+o5qwazFc/+/fttKcPbRAog0IT8V8fZgkfFa25ubqIc4jObAgg0IeTGG29U9tPZ+gOrrKy0pQ1v3RQwHugFCxYoDzNAffPNN7vlENttChgN9F9//UU6dOigBdAA9eLFi22pw1snBYwGeurUqdrADEBfeuml5OTJk055xLazChgLNNRrtr6f6nSdMWMGwptAAWOBhnrNOoFsj3X37t0JUmr2IyOBhjrNdkB0ux8xYoTZ1CbYvZFAQ51m3SCOj3fNmjUJ0mruI+OAhvrM8XDo+D4jI8NcahPs3Cigjx07Rtq2bRsJoOGPsKSkJEFqzXxkFNCPPvpoZGAGoC+++GLyxx9/mEmuy66NAXrbtm2Rgtn6mvT444+7pNbMZmOAvvPOOyMJNIBdW1trJr0OuzYCaKjDbH2iRfF69913O6TWzCYjgIY6zFEE2b6nVatWmUlw3K4jDzTUX7YnPqr3PXv2jEutmW8jDTTUXYb6y1GFOH5fxcXFZlJs23WkgYa6y/FJj/L7lJQUcuTIEVt6zbuNLNBQbznK8LrtLS8vzzyKbTuOLNADBw40EmgAvaqqypZis24jCfTbb79tLMwA9JAhQ8yi2LbbSALdrVs3o4EGqFesWGFLszm3kQN6zpw5xsMMQF9zzTXmUGzbaaSAhrrKUF8ZEoqvJPLCCy/YUm3GbaSAhrrKCPL/f8wtW7YkP//8sxkkn91lZICGesoI8/8wW1qMHz8egdZRAainbCURr03B3rx5s44p9RVzJD6hoY4yQtwUYrse2dnZvuDQcZD2QEP95MsvvxyB9vgf4bKyMh35ZI5Ze6CffvpphNkDZvi07tq1KzMcOg7QGugDBw4gzBQwW18/nn32WR0ZZYpZa6BHjx6NQDMA3bx5c/LDDz8wAaJbZ22BXrduHcLMALP1KT127FjdGGWKV1ugoV6ylSS8uv/C4aTNl19+yQSJTp21BBrqJDslCtvowM7KytKJUaZYtQMa6iNDnWSElw5eN52WLFnCBIounbUDGuojuyUJ2+kh79y5M2lsbNSFU+o4tQIa6iKDgwwSgS8+DcCZWFhYSA2KLh21AnrkyJHERAdZEDBZzsR9+/YFMb20ObUB+uOPP4591ZgwYYI0waKwsN2ZeN9990VhS7E9aAN0ZmZmDGj4rvzVV1/FNoE3bArEOxPXrl3LNoHCvbUAurS0tAnMAPSAAQMUllXd0JyciX369FE3YMbIlAca6h9DHWSnXzDKy8sZt2t2d3AmdunSxVHLRYsWRUIc5YGG+sdOMEObKQ4yUaQVFBS4annJJZeQv//+W9RS0uZRGmioe+wGs9VugoNMBB379+/31HL69OkilpI6h9JAQ91jC1y3qwkOMhGE5ObmemoJGu/cuVPEctLmUBZoqHfsBnF8e9QdZLx0VFZWUms5fPhw3uWkjlcW6F69elEnAQCPsoOMlxBWZ+JHH33Eu6S08UoCPXfuXCaYAej+/ftLE1Hlhf04E2+44QaVt5QwNuWAPnr0KElNTWUGGqBeunRpws2a9pDHmTh//nwt5VIO6Pz8fF8wA9DwG+s///yjZSKCCJrHmdiuXTvy+++/BxFWoHMqBXR1dbVvmAFoeM2aNStQwXSZHJyJliZ+r1OmTNFlu7E4lQIa6hr7Fd8+LmoOsli2GG5GjBghRMvt27czrCq/qzJAQz1jO5Q891FzkLFismbNGmFa3nXXXazLS+2vDNBQz5gH4vixUXKQsRKSkZEhVMv33nuPNQRp/ZUAGk6hxAPJ+z5KDjIWOkpKSoRree2117KEILWvdKChfjGcQuEF2Gl8VBxktIQkciY66cPS9sorr9CGIbWfdKDh9AmLsCx9wUF24sQJqQKHuXgiZyKLbk5927RpQ+rr68Pcjq+1pAINp06cxBPZ9uSTT/oSRrdBNM5EXl0nTZqkvCxSgYZTJ7wi04zftWuX8ongDZDGmUijlVefrVu38oYa6HhpQMNpEy/xRD3X3UHmRQCLM5FX08GDB3uFI/W5NKDhtAmvuCzjdXaQeRHC6kxk0c2p7zvvvOMVkrTnUoCGUyZOQgXZprODLBEdxcXFoWt59dVXJwpJ6rPQgYb6xHDKJEh43ebW1UHmRsiRI0dISkqKFC2fe+45t7CktocONJwucQMu6HZdHWRuhOTl5UnT8vzzzyc//vijW2jS2kMFGk6VBA2t1/w6Osic6KiqqpKu5UMPPeQUmtS2UIGGUyVewIXxXDcHmRMhopyJvHpv2rTJKTxpbaEBDadJeMUTNV43B1k8HSKdibya3n777fHhSX0fCtBwisStYg+voH7Hv//++1KF51lctDPRr4bWuOXLl/NsR+jYUIBOVLHHEiXsq04OMnvGg3Am8mp/5ZVX2kOUeh840DQVe3gF9TteFweZRQg4Ey+44AJlvrrZdX/mmWesMKVeAwcaTo/YN67SvS4OMouQIJ2JvHk577zzyPfff2+FKu0aKNBwaoRXqKDH6+AgAzo2b96svJYPPPCANJCthQMFGk6NBA2kiPlVd5BBsrKzs7XQ8vPPP7fYknINDGg4LSICtjDmUN1BVlZWpo2W/fr1kwKytWggQMMpETgtEgaMotZQ2UEWtjORV9M33njD4iv0ayBAwykRXlHCHq+qg0yGM5FX+06dOpHTp0+HDjMsKBxoOB3CK4is8c8//7yUJLgtKtOZyJuDp556ym1bgbYLB1pUxR5eQf2Mh994VXKQyXQm+tEvfszevXsDhddpcqFAi6zYEy9OWO9VcZCp4Ezk1fzee+91Yi7QNqFAw6kQXhFUGK+Cg0wVZyJvPj799NNAAY6fXBjQcBqEd/OqjJftIFPJmcibk5tuuimeuUDfCwEa6gjDaRDezas0XpaDrLGxkXTu3DlSWi5cuDBQiO2TCwEaToGoBKOIWGQ5yKC+tYj4VZqjY8eO5Pjx43buArvnBhpOf6gknshYwnaQQV1rkfGrNNe0adMCg9g+MTfQcPpDJeFExhK2g0xlZ6IIXXfs2GFnL5B7LqDh1IeIjao8x/333x+I8PGT6uBM5M1TTk5O/LaFv+cCumfPnpEHGpIYhoNMF2ciL9QffvihcIjtE/oGWkbFHl4x/Y4P2kGmkzPRr4bWuOuvv97On/B7X0BDxR447WEFacI1KAeZjs5E3nzPmzdPOMjWhL6AhlMevJvSbXxQDjIdnYm8ubvooovIb7/9ZjEo9MoMNJzu4N2QruNFO8h0diby5vCxxx4TCrI1GTPQcLqDdzM6jxfpIIO61TprwRt7TU2NxaGwKxPQcKqDdxO6jxflIIN61bprwRv/sGHDhIFsTcQENJzq4N1EFMaLcJBFxZnIm8+VK1daLAq5UgMNpzl4g4/KeF4HWZScibw57dGjhxCQrUmogP7pp5+UrdjDK6jf8X4dZFF0JvrV0Br38ssvWzxyX6mAHj9+PH46JyU10cCvgyyKzkQLTL/XCy+8kBw+fJgbZpjAE2gdKvb4FZJ3HKuDLMrORF4tH3nkkXCAhtMbvMFGeTyLgyzKzkQROd6yZQs31Ak/oeHUhohAozwHrYPMBGcib54HDRoULNBwaoM3SBPG0zjIoB61CVrw7rGiooILatdPaDitwRucKeO9HGRQh9oULXj3mZ6eLh5oqPMLpzV4gzNpvJuDrL6+3jhnIm/ei4qKfEPt+AkNdX55gzJtfFpaGmloaDgnESY6E3lzn5ycTOrq6s7RkqbhHKC/+OILhDnuN2faBE2ePLmJ5iY7E2k1c+s3bty4JlrSvjkH6KysLATaJ9CQHLuDzHRnohustO0bN26k5TjWrwnQS5YsQZg5YIZEWQ4ydCY2/ZdVWojt/W677bYYqLQ3MaCjWLHHLk6Y9+AgQ2ciP9CQs2XLltGy/F+/GNDfffcdgX+pwRe/BrW1taijQJZYiI4BzTII+6ICqiqAQKuaGYzLlwIItC/ZcJCqCiDQqmYG4/KlAALtSzYcpKoCCLSqmcG4fCnwL67cgi4AtNIQAAAAAElFTkSuQmCC[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALMAAACaCAYAAADit3kNAAAUO0lEQVR4Ae2dC5hOxR/H05JS6OIaEmJTiqUrZVMuS0UhSQgpQkqxyVOIJdSupyi3KPeUcktiQ0JsW4pNUrZnQ7RICEll/s9vH7P/2dk55z2X38yZ877zPs8+M+f2m+98f5/dmTPO8Z5DzMc4ECUOnBMl/dC2G7m5udpqizZhBmaJGV2/fj3p3bu3xBZMaNYBAzPrBnK9adOm5JxzziEbN25EjmzCiRwwMItcQdg3c+bMPJAB5ubNmyNENCEiOWBgjuSQh+Nnzpwh1apVy4cZgJ49e7aHSOYSNw4YmN245fDcoUOHFgAZYK5Ro4bDq81pXh0wMHt1zuK6Xbt2FQIZYIaf4cOHW1xldmM4YGDGcJGJ0blzZ0uYixQpQrKzs5mzTRXTAQMzopsrV660BJn+de7atStiiyYU64CBmXXDZ71hw4YRYQao09PTfbZkLhc5YGAWueJh36RJkxyBDDA3atTIQwvmkkgOGJgjOeTg+PHjx0n58uUdwwxAT5kyxUFkc4obBwzMbtyyOHfgwIGuQAaYK1asSE6ePGkR0ez24oCB2YtrzDVbt251DTLADD/JyclMJFP164CB2aeDbdu29QwzAJ2VleVTgbmcOmBgpk54KBctWuQLZIC5ffv2Hlo2l4gcMDCLXHG4r27dur5hBqCXLFnisEVzmp0DBmY7d2yOpaamooAMMCckJNi0ZA45dcDA7NQp5rwDBw6QkiVLosEMQKelpTEtmKoXBwzMHlzr06cPKsgAc+nSpcmhQ4c8qDGXUAcMzNQJh+WmTZvQQQaY4adfv34OVZjTRA4YmEWu2OxLSkqSBjMAnZGRYdO6OWTngIHZzh3u2Ny5c6WCDDC3atWKa9VsOnXAwOzUKUJIzZo1pcMMQM+fP9+FKnMqdcDATJ2IUI4YMUIJyABzfHx8BDXmsMgBA7PIFW5fTk4OiYuLUwYzAJ2SksKpMJuRHDAwR3KIENKtWzelIAPMxYoVI7t373agzpxCHTAwUycsytWrVysHGWCGnx49elioMrtFDhiYRa4w+26//fbAYAag165dy6gxVTsHDMw27kybNi1QkAHmxMREG4XmEOuAgZl1g6mfOnWKVKpUKXCYAejp06czykzVygEDs4UzgwcP1gJkgLlKlSrk9OnTFkrNbuqAgZk6wZTbt2/XBmSAGX6GDBnCKDRVkQMGZoErHTp00A5mAHrHjh0CtWYXdcDATJ04Wy5btkxLkAHmjh07cmrNJuuAgZl1gxDSoEEDbWEGoJcvX84pNpvUAQMzdYIQMnXqVFKuXDmtf8x/XM4kjKsamM8acvjwYdKzZ0/OHv02ly5dSiZMmKCfMA0UGZjPJqF///5504uPP/5Yg7RYS6hfvz657LLLyJEjR6xPitEjBmZCSGZmZv48+aabbtIWhfHjx+frfPrpp7XVGZQwAzMh5O67786HBG6yJk6cGFQ+LNv9/fffycUXX1xA59dff215fiweiHmYFyxYUAAQgLlMmTLk6NGjWvHw5JNPFtLZunVrrTQGLSbmYa5du3YhSADoAQMGBJ2b/Pa//PJLoUbQ+f777+efF+uVmIZ59OjRlpAAKFu2bNGCD34aBNroz7XXXquFRh1ExCzMe/fuJcWLF8+HgsLBljoM4++++66tRtA7ZswYHVgKXEPMwgxryiy4VvWFCxcGmqSrr746os4LLriA7Nu3L1CdOjQekzCvW7cuIiAU7jp16gSWp1GjRjnW+fjjjwemU5eGYxLmJk2aOIYEoB47dqzyfO3Zs4ecd955rnSuX79euU6dGow5mGfMmOEKEIA5iGH80Ucfda2zadOmOrGlXEtMwfzvv/+SqlWruoYEgO7Vq5ey5Hz22WeeNILOmTNnKtOpW0MxBfMLL7zgGRIAZcOGDUry53YaBNroT7Vq1ciZM2eU6NStkZiBeefOnfkJp4l3W6oYxr1Mg/h+DB06VDfOlOiJGZg7derkG2aARuYw/s8//5ArrrgCRedPP/2kBCCdGokJmFesWIECCMBcvXp1acO432kQ+xe6c+fOOnGmREtMwHzzzTejwQzADBs2DD05GNMgFmaor1y5El2nzgGjHmZ4nJNPMsb2rl27UPP60EMPoeu89dZbUTXqHiyqYT527BgpW7YsOiTwy4A5jMPbLRi/YKIYkyZN0p1BNH1RDfMzzzwjDRIAB2sYx54GsVCXL1+eHD9+HA0YnQNFLczffPONVJABmIYNG/rOraxpEAv0wIEDfesMQ4CohblNmzbSYQZg/Azj8DYLvNXCgiervnXr1jDw6EtjVMIMj23KgoKP62cYlz0NYrW2bdvWFyhhuDgqYb7uuuuUwQzAeBnGVUyDWJihvmjRojAw6Vlj1ME8btw4pSBTYNwO46qmQVQflHXr1vUMShgujCqY9+/fT0qUKBEIzG6GcZXTIBZmqKempoaBS08aowrm3r17BwIyBcbpMK56GkT1QVmyZEly4MABT7DoflHUwLxx48ZAQQZQnAzjQU2DWKD79OmjO5ee9EUNzM2aNQscZgDm1VdftUxEkNMgFmaob9q0yVJnWA9EBcyzZs3SAmSABIbx3NxcIQ9BT4NYoJOSkoQaw7wzKmCuUaOGNjADMKJhXIdpEAsz1OfOnRtmdgtpDz3Mw4cP1wpkCgw/jOsyDaL6oKxZs2YhIMK8I9QwZ2dnawkygNKiRYt8LnSaBrEwQ33EiBH5OsNeCTXMXbp00RZmAGXOnDl5fOg2DWKBjouLIzk5OWHnOE9/aGFOT0/XGmQABoZxXadBLNDdunUzMAfpADykA/8Phvnx7wFMg1avXh1kOlHaDuVf5smTJ+f9VY62u3GUjHoIAi/pNm7c2MOVel0SOphPnDhBKlSokAdzrVq19HIzhGrg5Vw65Zg2bVoIe/B/yaGDOTk5Od98SMLIkSP/3xtTc+UAvxpUqVIlcurUKVcxdDo5VDBnZWUVABlgjqa7cdVgiFaDBg8erFoGWnuhgrldu3aFYAago+VuHC2rDgKtWrVK6CX4uX37dgcR9DslNDAvXrzY0nxIQDTcjavEA17GBd9EPx06dFApBa2t0MCckJAgNJ4mIxruxtGyGiEQXQ2i3onKZcuWRYii3+FQwJyWlmYLMk1G2O/GVeDBrgZR30RlgwYNVMhBbUN7mA8ePEhKlSrlCOaw342jZtYi2KBBgxx5CYC/9tprFlH03K09zH379nVsPiQgzHfjshHZtm2bKy8vueQScvjwYdmy0OJrDXNGRoYr8+lw+f3336MZFE2BrFaDqG+isn///qGxQGuYW7Zs6QnmsN6Ny6Qm0mqQCGS6LzMzU6Y0tNjawjxv3jxPINMEhPFuHC2rgkD16tXz7Oc999wjiKjfLm1hjo+P92w+AB3Gu3FZeMD/lUF/yb2WCxYskCUPLa6WMKekpPg2H5IWtrtxtKwygdysBtmBXrt2bSaqnlXtYP7ll19I0aJFUWAO2924DETcrgbZAT169GgZEtFiagdz9+7dUUCmSQnT3ThaVs8G2rx5M6qXxYsXJ3v37sWWiRZPK5jXrFmDaj4FOix342hZPRvI62oQ9U1U9uzZE1smWjytYE5MTJQCc1juxtGySgjxuxokApnuW7duHaZUtFjawPzWW29JAZkmIAx342hZJYTAWzi079jlnXfeiSkVLZYWMP/999+kcuXK0syHZIbhbhwrq/D2DTbAfLy3334bSy5aHC1gfv7556WbD8nQ/W4cI6uYq0E8wOx21apV896Mx9CMFSNwmHfs2KEEZEgE3I3v2bMHyzst42CvBrEA83X4emSdPoHD/OCDDyqDGZKh8924XzBkrQbxELPbP/74o1/ZaNcHCvNHH32kFGSaBF3vxv1mFd62oX1UVXbq1MmvbLTrA4X5xhtvVG4+JLlJkyZoBuoSSPZqkN0vx4oVK7SwITCYX3/99UBApkmZMWOGFgnAEKFiNYj6Jirh65J1+AQC8x9//EEuvfTSQGHW8W7cKxCqVoNEINN9b7zxhlf5aNcFAvNTTz0VKMg0AbrdjXvJKrxVQ/sTZFm2bFly7NgxL11Au0Y5zF999ZUW5tPE79y5E83MIAKpXg2ivolK+J9Zg/woh/nee+/VCmad7sbdghDUapAIZLoPvkY5qI9SmN977z2tQKYJ0OVu3C0EN9xwg3Z+3nfffW67gXa+UpivueYa7cwHoHW5G3eT1aBXg+gfAlH5wQcfuOkK2rnKYB4zZoyWINNkTJw4Ec1U2YF0WA2ivolK+DrlID5KYP7111/J+eefrzXMcDd+9OjRIHLguk1dVoNEINN9r7zyiut++b1ACczwtNru3bu1/xk7dqxfP6VfD6tBH374ofZevvnmm+S3336T7gfbgHSYP//887y/yBMmTGDb1a7+8ssv5+kM8m7ciSmwGnT99dc7OTWwc+g0CL5eWeVHOsx33XVXHiRlypQhR44cUdk3x23BS5rweCgMkW3atHF8neoT2dWgIIZxp/1lp0HwNcuqPlJhfuedd/IAofOoAQMGqOqXq3Yee+yxAjoXLlzo6npVJ7OrQRdddJHyYdxJP/l/FGvevLmTy1DOkQbzf//9R6688soCkADUW7ZsQRGOFYROg+gvHJRB3Y3b9YlOg1idTzzxhN0lgRyDl4dZjVCfPXu2Ei3SYH7xxRcLdQo61rp1ayUdc9oIvJzJmw/b48aNcxpC+nl2q0FffPGF9PadNsBOg1hP4euWVXykwAxvH7Cd4eu6DOPwUiavjW6XKFGC7N+/X0UOIrbBT4OoRihVDuORhLLTIFYj1OFrl2V/pMD88MMPW0ICHatTp47sfkWMD19TLJoGsUno1atXxDiyTxBNg1iNUFc1jNv1VTQNYnUWKVKE/Pzzz3YhfB9Dh/mTTz6xBZl2MOg1XatpENVHS5V346JsWk2DqD4or7rqKtGlyvbBapCTfxTr2rWrVE3oMN9yyy2OYIZhfN++fVI7ZxU80jSIBaVZs2ZWYaTv51eDWF18/aWXXpKux6oBu2kQrzM9Pd0qjO/9qDDDv/rw4u22gxrG4bFPO138sVmzZvk22m0Aq9UgXhvdVjGMi/rgZBpENUJ52223icKg7EOD+c8//yTlypVzBQl0bsOGDSgdcRoEHvdkzXVSr169utPwaOc5nQax+mUP46LOOZkGsRqhPmXKFFEo3/vQYH722WddQwIdUz2MO50G8QlQcTdOs+lmGsTrlDmMU320tFsN4nWx2xUrViQnT56kYdBKFJi//fZbTyDTDqoaxuGlS9qmlzI7OxvNeLtAkVaD7LTLHMZZzU5Wg+x0Jicns+FQ6igw33///b4gUTGMw8uW8JinncGRjnXp0gXFdLsgTleD7LTKGsZZ3V6mQbzmrKwsNqTvum+Y4XFEXqSX7WHDhvnujF0Ar9Mgvi+rVq2ya8b3Ma/TIFanrGGcds7PNIjV2b59exoSpfQNMzyOyAr0U5c1jPudBrF9atSoEYrxoiBuV4NYXXxdxjBONbtdDeK1sdtLliyhYX2XvmCGxxBZYX7rsoZxeMnSrzb2+smTJ/s2ng/gdTWI1cXXv/vuO74Z39sY0yBWZ0JCgm9NNIBnmHNzcwk8hsgKw6hjD+PwciWGLjZGhQoVyIkTJ6iHKCXWNIjViT2MQ0cxpkGsRqiPHz8exUPPMMPjh7wojG3sYRxzGsT2b9CgQSgJgCCY0yBWI9Qxh3G/q0G8NrpdunRpcujQId9+eoIZHjukQmSUWMM49jSI7+u2bdt8JwAC+F0N4nWx21jDOMZqEKuLr/fr18+3l55ghscOeTGY2xjDOLxMeeGFF0rV2a5dO98JwFoNsvMfYxiXMQ3iNWdkZPjy0zXMc+bMkQoI7aDfYRxepqSxZJaLFy/2lQBZ0yC2z36HcZnTIFZnq1atfHnpGmZ43JAVILPudVEdHtuUqYuNXa9ePc8JkD0NYnX6GcaxV4NYXXx9/vz5nv10BTM8Zsg3LnPb6zAuexrE9zk1NdV1AmStBvHa2G0vw7iM1SBWE1+Pj4937SW9wDHM8JbAueeeqxRm6KjbYRzeuuANkr1dqlQpcvDgQeqpo1LWapBdX70M4yqmQbzmUaNGOfKQP8kxzI888ohySKCTbu/G4eVJ3hwV23379uW9tdyWvRpk1183w7jKaRCruVixYnn/Y5OlgRYHHMH86aefBgII7WBaWpqF/IK74TFNek0Q5ebNmwsKsthq0aJFYDqdDuMqVoPsctSjRw8L96x3O4IZHiu0a1j2MSfDOEyD4G0L2Vrs4iclJVk7ffaIqtUgO50pKSkRdapaDbLTuXbt2og62RMiwgyPE9o1qOpYpGEc3rJQpcWunXnz5rH+FqqrXA2y0lm0aFECX0ts9VG5GmSlEfbfcccdVhKF+21h/uuvv8jll1+uBSTQOau7cXi7ws4Ulcdq1aolNBp2ql4Nsuu33TCuejXITuf06dMt/eQP2ML83HPPaQMJdLhly5a8/rztoKdBfDJGjhxZSGdQq0G8NnZbNIwHsRrEauLrVapUIadPny7kp2iHJczw+CAfWIdtfhjXZRrEehMXF0dycnIK+B3UahCri68nJiYW0AgbQa0G8drY7SFDhhTSKdphCfMDDzygJczs3Ti8FAlvVbAd16XevXv3fL+DXg2y8wS+pph+dJoG8Zp/+OEHKtOyFMK8dOlSLQGhHaR34/A2Bd2nY7lmzZo843WbBrFeVa5cmcDXFeuwGsTq4usdO3a0hJgeEMJcv359rSGBu3F4boPvsG7bjRs3JlOnTtVeJwzjuqwG2eVw+fLllFthWQhm+A2FVQPdf+BrdnXXCPrgayV015mZmam9RuqhkOKzOwvBbHeyOWYc0NkBA7PO2THaXDlgYHZllzlZZwcMzDpnx2hz5YCB2ZVd5mSdHTAw65wdo82VAwZmV3aZk3V24H+sQ/nAlSO7TwAAAABJRU5ErkJggg==[/img][/td][/tr][/table][br][br][size=150]If we continue this process of removal forever, we are left with some points that never get removed from the triangle. The remaining points are what we call Sierpinski’s triangle. At any given stage, the triangle at the top of the figure is a scaled copy of the triangle at the previous stage.[br][/size][br][table][tr][td]stage 4[/td][td]top triangle[/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALQAAACYCAYAAABNo8N/AAAZUUlEQVR4Ae1dCfxNxftOtqhQ9uxlp7K0IUR2RSHJll3ZopAUlbUUKrJGlmwhW/bsShFlq4RSRLKEkIjz/zz33/n+3jv3nDlzZubce+79nvP5XHfmnDPPvPPO484785133uuM4Ao0kEAauC6B2uKrphw/ftxX8iQXYQJCe9DTmzZtMp555hkPkANIJw0EhHbSkMTzatWqGdddd53x+eefS5QOiqhoICC0ivYsyk6dOjVEZhC6Ro0aFm8Et7zUQEBojdq9du2aUaBAgSRCg9TTp0/XWEMA5aSBgNBOGnLxvH///mFkBqHvuOMOFwjBq6oaCAitqsH/yh84cCCCzCA0Pq+99pqmWgIYJw0EhHbSkODz5s2b2xI6RYoUxsGDBwWRgtdUNBAQWkV7/5VduXKlLZnNX+mWLVtqqCmAcNJAQGgnDQk8L1++vCOhQezVq1cLoAWvqGggILSK9gzDGDt2rBCZQegKFSoo1hYUd9JAQGgnDXGenz9/3siePbswoUHq8ePHcxCDR6oaCAitoMGePXu6IjMInTNnTuPixYsKtQZFeRoICM3TDufZzp07XZMZhMand+/eHOTgkYoGAkJLaq9BgwbShAapd+/eLVlzUIyngYDQPO3YPFuwYIESmUHoRo0a2aAHt1U0EBBaQnt33323MqFB6kWLFknUHhThaSAgNE87Fs+GDx+uhcwgdOnSpS1qCG6paCAgtAvtnThxwsCvc8GCBbV9Jk+e7EKC4FUnDQSEdtIQed6pUyfjm2++IXfUk40bNzZOnjypDhQghDQQEFqQCFu2bAmZGvXr1xcs4fzanDlzQphdunRxfjl4Q0gDAaGF1GQYtWrVSrKd58+fL1iK/1rx4sWTML/66iv+y8FTIQ0EhBZQ04wZM5KIh8ncnXfeKVCK/8rQoUPDMOvUqcMvEDwV0kBAaAE1FSpUKIx8IPWwYcMESlq/cuTIESNt2rQRmLNmzbIuENwV1kBAaAdVDRgwIIJ4IHT69OmNY8eOOZS2fty+fXtLzCJFilgXCO4KayAgNEdVhw4dMlKmTGlJPpBa5uyNjRs32uIBc9CgQRyJgkdOGggIzdFQq1atuOQDAd2evVG1alUuZurUqY1ff/2VI1XwiKeBgNA22lmzZg2XeCAzPtWrV7dBiLw9ZcoUIcw2bdpEFg7uCGkgILSNmipWrChEPpB62rRpNij/u3316lUjf/78wpjr1q37X+EgJayBgNAWqpo4caIw8UBokbM3+vXr5wqzcuXKFpIFt5w0EBCa0dClS5eMXLlyuSIfSM07e2P//v2u8YA5adIkRrog66SBgNCMhvr06SNFPhDQ7uyNZs2aSWHmyZPHuHz5MiNhkOVpICA00c7evXuliAcy49OiRQuC9v/JFStWKGH27ds3AjO4Ya+BgNBEN9j5ZpJT9nvVqlUE0TDKlSunjPn999+HYQYZew0EhP5PN0uWLFEmHv4T0LM3xowZowWzSZMm9j0YPAnTQEDo/9RRtmxZLeQDqceNG2f89ddfRrZs2bRhLl26NKzjgoy1BgJCG4YxYcKEEPlAQB2fkiVLhlY9dGCZGMHh6dYEZu8me0KfPn3aaNeuHasX3+UXL15sjBo1yndy+U2gZE/obt26hcyCZcuW+a1vwuQpU6aMkTlzZuPMmTNh94NMuAaSNaG3bduWZOPed9994ZrxUW7kyJFJcnbv3t1HkvlPlGRN6Lp16yYRBZO50aNH+66HTp06ZWTKlClMzu3bt/tOTr8IlGwJbTqo0vXmLFmyGGfPnvVL34Tk6Nq1axiZIW+9evV8JaOfhEm2hC5WrFgEUUCWHj16+KZ/tm7daikj5Jw7d65v5PSTIMmS0EOGDLElCsiyY8cOX/QRaxJBNvNTokQJX8joNyGSHaHtHFRNouDbD0P67Nmzk8hLZaPpN954w298irk8yY7QWHOmpLBLz5s3L6adU7RoUUc506VLZxw9ejSmcvqt8mRF6A0bNjiSxCQ4/toXq2vw4MHCcnbo0CFWYvqy3mRF6CpVqggTBcR+8803o95phw8fNtKkSeNKzk2bNkVdTr9WmGwIjVM+zV9f0e9YDOlt27Z1LWe1atX8yq+oy5UsCP3vv/8a+fLlc00UEL9jx45R65T169dLyQg5p06dGjU5/VxRsiD0K6+8Ik0UkGXz5s1R6UO3JhEdaQoUKGBcu3YtKnL6uZKEJ/S+ffuUyAzSRGNIlzGJKKGR7t+/v5+5FhXZEp7QTZs2VSY0yOLlkH7lyhUjb968WuSEh3lyvhKa0MuXL9dCEhD69ttv92xIVzWJ6C918+bNkzOfjYQmdKVKlQysVOj6DBw4UDtZfvzxR23yme1cvXq1djnjBTBhCY2toGvXrtXaDy+++KJx4MABrZgIR6H77A2ZU1G1NiqGYAlJ6HPnzhlZs2Y1dB6ntWfPnpD5onNIh5cMzAWdZ2+MHz8+hDl27NgY0ip2VSckoZ9//vkk2/mDDz7Qol1EfjVt1ZUrV2rBvP/++5MwdZy9cfHiRSNnzpwhzOzZsxvnz5/XImc8gSQcoRF2zSQevnPnzm38888/Sn2CiK8Us3z58kp4KAyTiGLqOHsDJhHF7Nmzp7Kc8QaQcIRG2DXaqUi/9NJLSv0CB1UWU2VIh1cMvGNYTJWzN0yTiMXcuXOnUtvjrXBCERpbPtkONfOyQzp1UDWx8K0ypFOTiGLee++90vyhJhHFbNCggTRmPBZMKEIj3BrtTJp+8sknXfcPIrxmzJjRFlNmSGdNIioj0jJnb7AmEYu5YMEC122P1wIJQ2iEWWM7ks1/+umnrvoJS2osBpt3O6RbmUQUU+bsjdKlS3PlRHzy5HIlBKERXg1h1igxrNJuhnREdrXCYO+5GdJ5JhHFdXP2xogRI4TkHD58eLLgdEIQGn9IoITgpd977z2hjkVkVx4OfSY6pPNMIoqHtMjZGydOnOCaRBTz5ptvNv744w+htsfzS3FPaIRVox3nlL711luNP//8k9tniOjqhEOfiwzpIiYRxRRx1BUxiShmp06duO1OhIdxT2iEVaOdJpJ+7rnnuH2HiK4iOPSdt99+2xZT1CSieEjzzt4QNYlYzC1bttjKmQgP4prQCKfGdpho3m5IRyRXUQz6Hob048ePW3LCjUlEMXmOurVr15aSs1atWpYyJsrNuCY0wqlRArhJP/rooxF9iAiuiOTqBoe+azWkuzWJKB7SVo66M2fOlJYRmDNmzIhoe6LciFtCI4wa2/lu8x9//HFYPyKCq1sM9n12SJcxiSimlaOujElEMQsVKhTW7kTKxCWhET6NdpBsmh6nhcitsji0XM2aNZP4oWISUUx69oasSUTxkB4wYECSnImUiEtCI3wa20GyefM4LWw1lcVgy3300UchjqiYRCwmzt745ZdfjFSpUmmRM2XKlMahQ4cSicuhtsQdoeGNwXa2Sv6GG24IRWxVwWDLYkjXYRJRXDjqtm7dWmvbW7VqFRA61hrAxh6csxF81HUAk2jNmjWx7lKt9cfVLzTCpeFXK5Fn6Vp71wEMjr/wu0ykK24IfeHCBSNHjhwhQhcuXDiR+iAmbXn11VeTzJeJEyfGRAYvKo0bQvfu3TupA/Ar7YUHthcK9iMmu0qUK1cu49KlS34U1bVMcUHo3bt3h5EZhE7UWbrrHpQoYLVK1KdPHwkk/xWJC0I3bNgwgtAgdSLO0r2myKpVqyx1CX3u3bvX6+o9x/c9oRcuXGjbAeiERJule93jcPCF3qw+jRs39rp6z/F9T2gnb4xEm6V72ePmKpEVmc17S5Ys8VIEz7F9TWhRb4xEmqV71eN0lcgkr9V32bJlvRIhKri+JTS8MTJkyGA5NLIdkUizdK96vVevXkK6hG7fffddr8TwHNe3hO7cubNwB6ATEmWW7kWP79q1y5Uub7nlFuP06dNeiOI5pi8JLeuN8d1333musHiswG6ViB3paL5bt27x2FR/Hqcr642RCLN03SxyWiWiJGbT27Zt0y2O53i++4VW9caI91m67h4vVaqUK3ODkvqRRx7RLY7neL4jtKo3RrzP0nX2OM7ioASVSc+ZM0enSJ5j+YrQurwx4nmWrqvH3awS8YherFgxXSJFBcc3hNbpjRHPs3Rdve52lYhH6iFDhugSy3Mc3xBatzdGvM7SdfS47CqRHanTpk1rHDlyRIdonmP4gtCIhTJ//vzQiUY41UjHB2HY4nGWrqPHEVVLhw4pRrzEQPQFoeGgetddd+noyxAGIqrCGyMeZ+mqSjBXiUxHXVU8lIcjMX69N2zYoAPOU4yYExoxUMyh7q233tLSWOqNEW+zdFUFwJsH+ixYsKAqVKj8b7/9ZsCRGJhVq1bVguklSEwJjdgniIFiEvqmm24yfv/9d6X2IuyaiYfveJulqzQeXjy07TrO3mjfvn0Y5ocffqgioudlY0poxD6hHYD0s88+q9RohF1jMeNpli7beKtVouuvv974+eefZSGNjRs3RugyX758IY97aVCPC8aM0Ih5whLPzH/xxRdSzUa4NRODfmOWfvjwYSnMeClkt0r09NNPSzfh4YcfttQnJp1+vWJGaMQ8oaSj6Ro1akjpi+eN0a5dOynMeCiEVSKqPzb92WefuW7GlClTuJgI6ezHKyaERqwTVuls3u0sHWHWWAw2Hw+zdBmSwGuHbSvNV6xY0RXs1atXjQIFCnAxmzZt6gozWi/HhNCIdUIVbpV2M0tHxFSEWbPCofeqVKkSLb1GrR66SkTbyqYnTJggLBPWnNnyVvnly5cLY0brxagTGjFOrJRjde/1118X0gPCq1mVt7o3efJkIcx4eIldJbJqr3nvtttuM/7++2/HZu3fv19Ylwjt7LcrqoTGX54Q48RUstM3Zuk//fQTV2cIq+aEQ5/7fZbObSzz0GqViLaVTSN0stPVrFkzV/p8//33nSCj+jyqhEZsE1bJTnmnWTrCqjlhsM/9PEsX7X1457DtEsnzzt6wWyXi4WbNmtU4d+6cqNievxc1Qn/99ddSHQBl2s3SEU6Np2zes3379nmuXC8r4K0S8dr9xBNP2IpVrlw5KX3iRFi/XFEjNGKa8BTNe2Y3S0c4NV453jO/ztJFiCGySsRr++LFiyOqGTNmjLQuURdCPvvhigqhEcuEp2CRZ+wsHWHURMrx3vHjLF2EFPfcc49S28uUKRNWzV9//SW0SsTT5WOPPRaGGatMVAhdvHhxpQ6AIuksHeHTEEaNp2CRZ36cpTsRwc0qEU8H77zzTlJVblaJeJjYAhzry3NCm1sPeYoQfWbO0hE+TbSM03ujR4+OdR8I1+92lYjX9kyZMhmnTp0y3K4S8TAR+jnWl6eEplsPeYpw8wxh09y87/QuZulnz56NdT8I1S+zSsRrf9euXQ2ZVSIepq4twEIKsXjJU0JjlxuCWer8HD16VCseZLMKbmmhq5jewirRJ598or3tOvsGWJhcqm4BVlG0Z4Q2tx6OGjVKRT7Pyw4dOjT0i++XWbpdg7FKpNOrx64elfumSYRQ0LG6PCO0ufUwS5YsxpkzZ2LVPm69cPzE1lIMofXr1+e+G8uHdJUo1kM6Tw/UJEJI6FhcnhCa3XrYo0ePWLTNsU7WG2PevHmOZWLxAl0l0uHV40Ub2D+cyW4BVpVNO6Gx9TB//vwRE7cdO3aoyqq1vGkS0QmOH2bpbCNNk4jKqerVw9ahIw+HZCoj0tOnT9cB7QpDO6H79esX0TA0rl69eq4E8/plOHyyHYD8sGHDvK5aGJ+3SiTr1SNcuYsXqUlEdYrQ0NG+tBIaXgy0QWzaL0M6HD1Z2cx8+vTpjWPHjkW7HyzrY00iU0Z8x2pItxKUmkRURqQRIjqal1ZCO209LFmyZDTbZlkXQipbmUS0Izp27GhZNpo3rUwiKiPSsRjSWR1YmURUzhQpUjhuAWYxVfLaCL1ixQrbXz3awFiv+dqZRFRGpGM1Szc7084konK68eoxcXV+Y5XIPLODysWmW7ZsqbNaLpY2Qj/wwANChMaQjj+OxOJyMoloR1SvXj0WIobqZFeJqFxsWtSrx4vG8EwiVs7Vq1d7IUIEphZCu916GKshHVtGWUXz8tOmTYtQmNc37FaJ7OSM9pButl/EJKIyP/jgg2ZRT7+VCY2th9myZXNFFDR08+bNnjaMBcdWUapgkTTOx4v2JWoSUfmjOaSb+hAxiaiMSI8fP94s7tm3MqFfeOEF10RB46I9pIuaRGwnRHOW7sYkYuWM1pAOJvJWiVi5aD5nzpzGxYsXPSMzgJUI/e2330qR2WxktIZ0OHKadcp8Hzx40NNOMMGdVol4skdrSBdZJeLJ2bt3b7O5nnwrEfrxxx9XIko0hnQ4cGKLKE/JTs9atGjhifIpqOgqEU/WaAzpMiYRK/Pu3btp07WmpQmNrYysoDJ5HH3r5SVrErFtWbVqlZdiGrImEZXT6yFdxSSicjZq1MgzXUoTGlsZqZAqaa+GdFWTiLapQoUKnnWC21UiKheb9nJId7tKxMpG84sWLfJEn1KExhZGKpxq2qshHY6bqrLR8uPGjdPeCbKrRFQuNr1nzx7tcuowiaicpUuX1i4jAF0TGg6qiF+Cg050fRALRfeQDodNXfKZOPA8v3DhgtaOQAg6E1/XN+IT6r7gVKtLPhOH9eTXIbNrQmPrYp48eYzLly/rqD+Ega2Huod0mERNmjTRJiMcSuFY2qtXL22Ypkmk06sHZ27gl1DnkG6uEun06oHDc8aMGY2TJ09q0yeAXBEaWxbNYaNv375aBEEMFBNT15BOTaKlS5dqkRMOpaacu3bt0oJprhLp9OrBmRuQU9eQTleJdHn1wCQyddmlSxctujRBXBEaWxZNQfCNU/hVL8RAMTFz5MihPKTDQfPGG29MwsTRvarX1q1bk/Aga8OGDVUhQw6vZrvxrcOrB2YBxRw5cqSynOwqkY4twFjloHIirqKuS5jQOICcCoE0zldTueAVzmKqDulw0GQxVYf0unXrRmAuXLhQpekhh1dWThWvHtMkopiqQ7ppElFM1S3ApklEMevUqaOkS1pYmNDYqkiFMNOyQzp1UDWxzG/ZhXds+TQx6HfmzJmlHXVnz55tiVmqVCmqR1dpahJROVW8eqhJRDFVhnS7VSKVLcCmSURlRHrWrFmudGj3shChsUWRFcDMyw7piHliYrDfskM6axJR3O7du9vpgHu/aNGitnLKrCZglQiOrlQ2mpYZ0lmTiOIhLTOkY5WIxTHzsl49MIFMDPa7SJEi3H4QfehIaBw4joPHWQFoHuetubkQ64SWt0q7HdLhvWGFQ+9t377djZjG4MGDuZgZMmQwTpw44QoTq0RUJjYtM6RjyGZxaF5mSHf6w5nbLcBYzYAJROVi09C36uVIaBw4zlbM5nEqPw4ZEb1Eth66naXDIZOVi827GdIRBi5NmjSOmJ07dxZttkFXiVjZaN7NkG5nElE8pN0M6XYmEYvpZguwnUlEMVOnTh06GUpYoRYvcgmNg8Zphby06JDuZuvhiBEjLESOvIUtnjzZ6LO5c+dGAljcadu2rTDml19+aYEQeatmzZpCmG6GdJ5JRNstOqSzq0QUg01Xq1YtspEWd5xMIorbpk0bCwTxW1xCY0sircwp7TSkY+shYpw44ZjPRYZ0mETw2jDLOH2XKFHCUTvr168XxkN9tWrVcsS0WiXiySoypDuZRCz+oEGDHOW0WiVicWgefzV2uqxWiSgGm163bp0TpO1zW0JjKyJbkVMe56/xLpmth05DOrw1nORinzsN6Qj/xpZxys+cOZPX9FAweScM9jlvSMfBiBii2TK8fKpUqQyEULa77FaJeJhOW4BFTSJax0MPPWQnouN9S0Ij/BcOGKeViKZx6IjVpbL10G6WDi8NUbnoe+nSpbN11EXYN/quaLpw4cJWzQ7d460S8fB5Xj1uTCJaB29I560SUQw2zdsCLGoSsZiTJk2y1SfvgSWh8Xd2tgLRPA4dsbpUth7Wrl3bCtJwaxLRNnTo0CEC88qVK0bevHml2z5w4MAITJFVIioXm7by6nFrErGYVkO6yCoRi0PzBw4ciGi7W5OI4snuF4ogNP07O63ATRqn9tNLxkGVrY8d0mVMIhaTHdJffvllaTIDO2XKlMahQ4do0w2RVSJWLpq3GtIxJNN33KYrV64cJiMyIqtEvHqaN28ehim6SsTDlNkvFEFohP3iVSLyDIeP4Fw289LhjUFn6XC0hHeGiCy8d+gs/YcfflDGQ12tW7c2mx0KR8erX/QZHdIxFIuW472HkMrmJWsSsfh0C7CsScRiol/cXGGEtvo7O1uBaB6HkOAytx6KluO9Z87S4ZXBe8/NM3OW/tRTT2nDXLt2bajtKiYR2wZ49WDLLoZi9plMPnfu3AZCK7tdJeLVVb58+VC7VU0iWofbLcBhhLb7OzutwE0ah5HInNlhVwdm6djnYfdc5j6G9GXLlmnFrFSpkoHN6zLy2JWBV4+qScRiY0iXWSVicWh+7NixhswqEcVg0272CyURGv9TsZqg8wN7XCcesODtoBsT+5t1Y2IzvG5MePboxNSNB9mwY1CnjCZW6Kdf4J8kQgu8G7wSaMD3GggI7fsuCgR0o4GA0G60Fbzrew0EhPZ9FwUCutFAQGg32gre9b0G/g+9ypDNk/nSfQAAAABJRU5ErkJggg==[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJwAAACJCAYAAADZo1FlAAAKwElEQVR4Ae2deagNYRjGb7KXCJGSZIks2bKXLbKFyBr+QHayJLqWSPZEIUsh67VnFxKykz1L9izZ12tfR8/JOc2dO3Pmm5nvuu+883413Vmf877f87tnzjnzLSmGFF818Pv3b1/XRf2ilKhXgJ/8P3z4YKSlpfm5NPLXCHA+EBg7dqyRkpJipKen+7g62pcIcB79v3v3bgw2AJeamurxajldgPPIQKNGjRLAAbr79+97VIj26QKcB/8PHz6cATYA17RpUw8KcqoAp8jAjx8/MsEG4LAcPXpUUUVOE+AUGViyZIkjcDly5DAApBT3GhDg3OvIeP36tSNs8Xe5ZcuWKSjJKQKcAgMDBgxwBQ7gvXnzRkEt2qcIcC7+X79+XQk2ADdo0CAXNTkswLkwUKVKFWXgAN2NGzdcFKN9WIBL4v/u3bs9wQbgqlevnkRRDglwDgx8/frVM2wADsvevXsdVGW3AOfAwJw5c3wDB+gArJTMNSDAZa4T4+nTp4FgA3Bz5861UZZdApwNA126dAkMHKB79uyZjXq0dwlwFv/Pnz+vBTYA16NHD4u6bApwJgbQirdevXpGuXLltC2XL182vYKsCnAmBjZu3GhcunTJtCf4au/evY0/f/4EF2KiIMD9M/Ljx4+xW2mHDh20Wbtp06aY5ubNm7Vphl1IgPvn4IQJExKf3bZt26bF10qVKiU0P336pEUz7CICnGEYDx48SICBD/tVq1YN7OvMmTMzaE6ePDmwJgcBAc4wjBYtWmSAA9Dhh1+/5cmTJ0aePHkyaT58+NCvJJvrIg/csWPHMoEB4PLnz+/7d7T+/fvbarZq1YoNOH4TiTRwP3/+NHLlymULB6Dz09zICWDoYTlx4oRfr1hcF2ngli9f7ghbHJCTJ096MrpZs2ZJNfHO+evXL0+anE6OLHBv375NCkYcOHy+Uy2rVq1S0ly5cqWqJLvzIgvc0KFDleAAeGvWrHE1Hk8pSpcuraz57t07V02OJ0QSuJs3byqDAeDKli3r6v2kSZM8aY4YMcJVk+MJkQSuVq1anuAAdFOmTHH0/86dO571oHnr1i1HTa4HIgfc/v37fcEBQO7du2fLQc+ePX1p1q1b11aP885IAfft2zdfYAA2LHgQby1BAIbmwYMHrZKstyMF3Lx58wIBZwdI/fr1A2t+//6dNWTm5CID3PPnzwODAeAaNmyYqL/Fixdr0VywYEFCk/tKZIDr1auXFjgA3dKlSw00ZypWrJg2zZcvX3JnLZZfJIC7cuVKDA4AomNB52h8a9WhFdcYMmSIAMehBtDadvDgweRT2bVrl4F/DO6F/TscGlPiNrhv3z7SXtasWdMoX748++borIFDK1vAhqVOnTpkgZs/f34izu3bt5ONU0dgrIHD56w4cPi7aNEiHXWmVQNDfBUqVChDnJ8/f9b6GpTE2AL36NGjDCYCuKJFixqYY4FSGT58eKY4p02bRilErbGwBa5t27aZjAR0o0aN0lqBQcTOnTtnGyPifPz4cRBpsteyBO7UqVOORsLMixcvkjDE6Z8CMersrkgi2X9BsAMOrWkLFCiQFLj27dtnuwfodA2wki1nzpzJ9jh1B8AOONVWt1u3btVdl570KlasmBQ2gFi4cGGD2yRyrIB7//69q4nxdxQ8LciuMn36dOU4165dm11hZsnrsgIOXwjiQKn8nT17dpZUajJRfBnInTu3pzipfbNOlp/bMTbA3b5925OJADJfvnyxwQfdKknn8X79+nmOE7MXcilsgPPbLm3gwIH/zUtMkaTyzmt3DmYx5FBYAHfo0CHfRsLc/9U5GRPB2cGksg+zGHIooQcOrWVVDEt2TvPmzbPcS/RFTRaDyjHMZhj2Enrg8HxUxSy3c1avXp1lXmJIiVKlSmmJM+yTyIUaOLSSdQNJ9XiZMmWyrGnQxIkTtcWJWQ3DXEINHCZdwzdNXUtWPDTHt2dd8cV1MLthWEtogbt69aqh+zPNuHHjDN3fBocNG6Z9LtWpU6eGlTcjlMCh2XiFChWMxo0ba6v4a9euxW576Gyjq6CVMW7p48eP1yVpYF5WaGKWwzCWUAK3Y8eOxGciDLmlo3Tu3DmheeDAAR2SBnrWxz9DYjyToOXLly9GiRIlYprZ+WguSB6hAw6VHjcRf0uWLGkE7Ui8c+fODJoNGjQIUqexa63fnrt37x5YE7d8c+6Y7TBsJXTAzZgxI0Olw4DU1NRA9Y4OLGYjsR7k2yCefaJ1sVUzyCyD8Vu+VTNsk8iFCjgM1myt8Pi231uWuQNLXAt/ixcvbvgd6n706NG2cdauXdv3P4b5lm+OM8jg176DCXBhqIDr2LGjrZEwoFu3bp6rAT8vFCxY0FFzzJgxnjUxk40ZCOv6woULPWtab/lWTcx+GJYSGuDOnj2b1EiYsGfPHk/1jp8srOZZt712TkbTcKuGebtIkSIG2u15KTVq1Eiq2bVrVy9y2XpuKIBDq1e7z0RmI7Hu5ZalAjA0O3XqpGwQWhFbY7LbHjlypLKm6ohPmAUxDCUUwK1fv17JSJirOhJRmzZtlDVVOydjBhs7wOz2XbhwwZWPV69eJb3lm3Xxc0kYmqOTBy49PV3ZRBiAfgBuAzZv2LDBk2a1atVc4fA6ZblKRx6VW74ZOnTMoV7IA2f97clcwU7rbgM24ymF07VO+5NNKY6ZnzH/gtO1Tvu3bNniyIfqLd+qjWHEKBfSwGFMXWuFqm473bLwgF5Vw3weuh6+ePHC1kvMWGM+V3U92dOC1q1b+9JEyxTKhTRwTZo08VXpMLxdu3aZ6h3DPySb6sgNFLsx3DBTjdt1yY7bdeRJS0sLpInZEakWssAdOXIkUKXDZOvEuH379g2sefr06Qxe2s1EmAww6zE0ObL+jubnlm/W9TJ7ToZk/sMGSeDQqtVcgX7XK1eunKhCHQAjjpYtWyY0MUON39jM16FdX7z4veWb9bCOSeYoFpLAYQxdawX63Z41a1as3tGUya+G9bp169bFNDFDjfWY3+3jx48bmE81Z86cWjTR9xVN26kVcsBhvDS/ptldlzdvXmPFihVaNTFSpXXsObvX9rIPHXn69OmjNU5dTbd0QksOODSuxA+YsuipA52w6NAiB5yOpESDbg0IcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJCXB0vWEZmQDH0la6SQlwdL1hGZkAx9JWukkJcHS9YRmZAMfSVrpJ/QUM6z2taJz9jgAAAABJRU5ErkJggg==[/img][/td][/tr][/table][br][br][size=150]For the completed Sierpinski’s triangle, though, the top triangle is a scaled copy not of the previous stage, but of the full Sierpinski’s triangle.[/size][br][br]For the completed figure, what scale factor takes Sierpinski’s triangle to its scaled copy at the top?[br]
Based on the scale factor, what fraction of the original shaded region should be contained in the scaled copy at the top?[br]
The scaled copy at the top actually contains [math]\frac{1}{3}[/math] of the shading of the original. Provide reasoning that shows that this is true.[br]
IM Geo.5.6 Practice: Scaling Solids
[size=100][size=150]It takes 2 ounces of paint to completely cover all 6 sides of a rectangular prism box which holds 15 cups of sugar. Double the dimensions of the box.[br][/size][br]Approximately how much paint would the new box need? [/size]
How much sugar would it hold?
[size=150]A solid with volume 12 cubic units is dilated by a scale factor of [math]k[/math]. Find the volume of the image for each given value of [math]k[/math].[/size][br][br][math]k=\frac{1}{4}[/math]
[math]k=0.4[/math]
[math]k=1[/math]
[math]k=1.2[/math]
[math]k=\frac{5}{3}[/math]
[size=150]A solid’s volume is 10 cubic inches. The solid is dilated by a scale factor of 3.5. Kiran says, “I calculated the volume of the image as 35 cubic inches, but I don’t think that’s right.”[/size][br][br][size=100]What might Kiran have done wrong?[/size][br]
[size=100]What is the volume of the image?[/size][br]
Plot the points in the table on coordinate axes and connect them to create a smooth curve.
A parallelogram has an area of 10 square feet. Complete the table that shows the relationship between the dilated area (x) and the scale factor (y).
[size=150]A figure has an area of 4 square units. The equation [math]y=\sqrt{\frac{x}{4}}[/math] represents the scale factor of [math]y[/math] by which the solid must be dilated to obtain an image with area [math]x[/math] square units.[/size][br][size=100][br]Select [b]all [/b]points which are on the graph representing this equation.[/size]
[size=150]Tyler is designing a banner that will welcome people to a festival. The design for the banner has an area of 1.5 square feet. The actual banner will be a dilation of the design by a factor of 5. W[/size][size=150]hat will the area of the actual banner be?[/size]
[size=150]The horizontal cross sections of this figure are dilations of the bottom rectangle using a point above the rectangle as a center and scale factors from [math]\frac{1}{2}[/math] t[/size][size=150]o 1.Sketch an example of a cross section that is created from using a scale factor of [math]\frac{3}{4}[/math]. Label the dimensions of the cross section that you sketch.[/size]
A regular hexagon is inscribed in a circle of radius 1 inch.
[size=100]What is the area of the shaded region?[br][/size]
[size=100][size=150]Two distinct lines, [math]\ell[/math] and [math]m[/math], are each perpendicular to the same line [math]n[/math]. Explain why [math]\ell[/math] and [math]m[/math] are parallel lines.[/size][/size]