Asintoti
Introduzione al concetto di asintoto: definizioni e tipologia.
Table des matières
- Definizione di asintoto
- DEFINIZIONE DI ASINTOTO
- Asintoti verticali
- ASINTOTI VERTICALI
- ESEMPI
- Asintoti orizzontali
- ASINTOTI ORIZZONTALI
- ESEMPI DI ASINTOTI ORIZZONTALI
- Asintoti obliqui
- ASINTOTI OBLIQUI
- ESEMPI ASINTOTI OBLIQUI
- Verifica finale
- Ora tocca a te!
DEFINIZIONE DI ASINTOTO
Una retta r è detta asintoto della curva [math]y=f\left(x\right)[/math] se la distanza di un punto [math]P\left(x,y\right)[/math] di questa curva dalla retta tende a zero quando il punto indicato si allontana indefinitamente sulla curva, cioè quendo almeno una delle coordinate del punto considerato tende all'infinito.
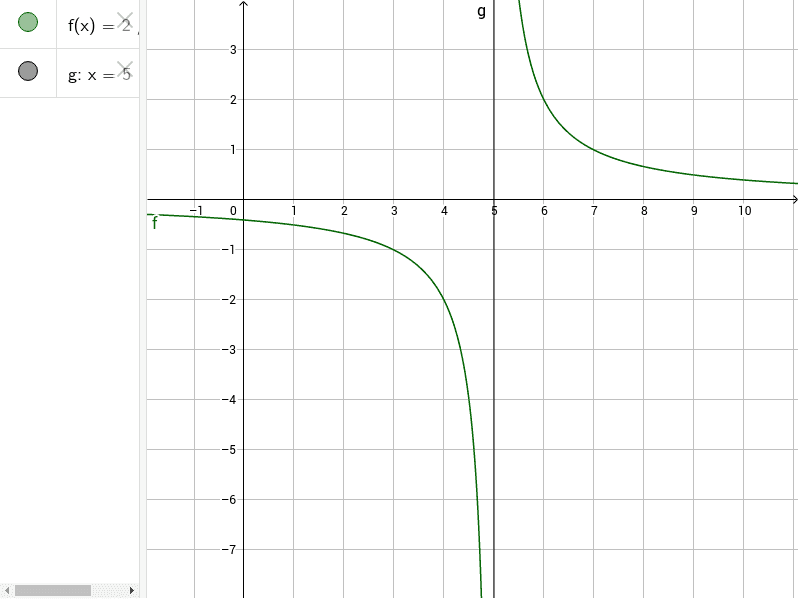
ASINTOTI VERTICALI
Se [math]lim_{x\longrightarrow c^-}f\left(x\right)=\pm\infty[/math] o [math]lim_{x\longrightarrow c^+}f\left(x\right)=\pm\infty[/math] o entrambi,[br]allora la retta [math]x=c[/math] è un [b]asintoto verticale [/b]per la curva.
Infatti la distanza di un punto [math]P\left(x,y\right)[/math] della curva dalla retta [math]x=c[/math] vale:
quindi quando x tende a c questa distanza
ASINTOTI ORIZZONTALI
Sia [math]lim_{x\longrightarrow\infty}f\left(x\right)=k[/math][br]Allora la retta [math]y=k[/math] è un [b]asintoto orizzontale [/b]per la curva
Se [math]P_1\left(x,k\right)[/math] è un punto della retta [math]y=k[/math] e [math]P\left(x,f\left(x\right)\right)[/math] è un punto della curva, la distanza [math]P_1P[/math] vale:
Allora il [math]lim_{x\longrightarrow+\infty}P_1P[/math] vale
ASINTOTI OBLIQUI
Se [math]lim_{x\longrightarrow\infty}f\left(x\right)=\infty[/math], se esiste un asintoto per la curva, questo deve essere una retta [i]r[/i] obliqua rispetto agli assi cartesiani e perciò dovrà avere un'equazione del tipo [math]y=mx+q[/math] ed inoltre dovrà essere [math]lim_{x\longrightarrow\infty}PH=0[/math], dove [math]P\in f\left(x\right)[/math] e [math]H\in r[/math][br]Se i seguenti limiti esistono e sono finiti:[br][math]m=lim_{x\longrightarrow\infty}\frac{f\left(x\right)}{x}[/math] [math]q=lim_{x\longrightarrow\infty}\left[f\left(x\right)-mx\right][/math] [br]i loro valori ci danno coefficiente angolare e intercetta dell'asintoto obliquo alla curva. [br]
Ora tocca a te!
Sia data la funzione[math]f\left(x\right)=\frac{ax^2+3x+1}{bx-1}[/math] con [math]a,b\in\mathbb{R}[/math] parametri.[br]Stabilisci le condizioni per [i]a[/i] e [i]b, [/i]affinchè la funzione abbia asintoti verticali e orizzontali/obliqui