So oder so ähnlich soll die Wertetabelle im RH aussehen.[br]
1.1 Die Normalparabel
Eine neue Funktion: Die Normalparabel
Bisher habt ihr lineare Funktionen betrachtet und mathematisch beschrieben. Heute lernt ihr eine neue Funktionsklasse kennen: Die quadratischen Funktionen. Das erste und wichtige Beispiel dafür ist die Normalparabel. Hier ist der Graph der Normalparabel aufgezeichnet.
Graph der Normalparabel
Aufgabe (ÜH):
Lies die Punkt A-E aus dem Graph der Normalparabel ab. [br][br]Wie bestimmt man die Koordinaten eines Punktes im Koordinatensystem? [br][br]H ist ein Punkt der nicht auf der Normalparabel liegt und uns hier als Beispiel dienen.[br]Die Koordinaten des Punkts H lauten:[br]H (1 | 10) (gesprochen "1 Strich 10")[br]Der erste Wert in der Klammer beschreibt als den x-Wert des Punktes und der zweite Wert in der Klammer beschreibt den y-Wert in der Klammer.
Überprüfung der Punkte. Kreuze alle richtigen Koordinaten an.
RH
Stelle eine Wertetabelle für die x-Werte von -4 bis 4, deren y-Werte zur Normalparabel passt. [br][br]Tipp: Überlege dir zuerst wie die y-Werte für die positiven x-Werte lauten.[br][br]Die Überschrift dazu lautet: [u][b]1. Die Normalparabel[/b][/u]
Beschreibe, wie die x- und y-Werte der Normalparabel zusammenhängen. [br]Stelle einen möglichen Term auf der die Normalparabel beschreibt. [br]Begründe, warum bei diesem Term die Normalparabel als Graph herauskommt.[br][br]
RH
Zeichne einen Graphen zu erstellten Wertetabelle in dein Regelheft.[br][br]Um einen genaueren Graphen zeichnen zu können, sind Zwischenwerte sinnvoll. Diese sind in der folgenden Tabelle abgebildet.
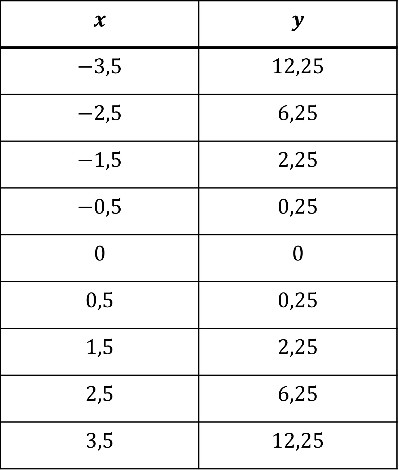
Wertetabelle für weitere x- und y-Werte der Normalparabel[br]