フロベニウス法でベッセル
第1種 整数m次ベッセル関数 Jm(x)
1。フロベニウス法とは
[size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br][/b]前回まで、べき級数を利用した微分方程式の解法を見てきた。[br]今回は、べき級数の拡張版であるフロベニウス法でベッセルの微分方程式を解こう。[br][b][br][size=150][b]<フロベニウス法はべき級数法の拡張版>[/b][/size][br][/b][/size]p(x),q(x)がx=0で解析的なとき、[br]微分方程式B=[math]y''+\frac{p(x)}{x}y'+\frac{q(x)}{x^2}y=0[/math]の係数は解析的ではない。[br]だから、x=0は確定特異点という。[br]解の1つはy=Σa[sub]m[/sub]x[sup]m+r[/sup]=x[sup]r[/sup](a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+....)=a[sub]0[/sub]x[sup]r[/sup]+a[sub]1[/sub]x[sup]r+1[/sup]+a[sub]2[/sub]x[sup]r+2[/sup]+.....(a[sub]0[/sub]≠0)rは複素数。[br]これとは1次独立な解をもつ。[br]係数が解析的でなくても、解くことができる、べき級数法の拡張版といえる。[br]まず、級数の形にしてみよう。[br]y'=ra[sub]0[/sub]x[sup]r-1[/sup]+(r+1)a[sub]1[/sub]x[sup]r[/sup]+(r+2)a[sub]2[/sub]x[sup]r+1[/sup]+....[br]y"=r(r-1)a[sub]0[/sub]x[sup]r-2[/sup]+(r+1)ra[sub]1[/sub]x[sup]r-1[/sup]+(r+2)(r+1)a[sub]2[/sub]x[sup]r[/sup]+....[br]p(x)=p0+p1x+p2x[sup]2[/sup]+.....[br]q(x)=q0+q1x+q2x[sup]2[/sup]+.....[br]Bの左辺にx[sup]2[/sup]をかけて展開しよう。[br]x[sup]2[/sup](r(r-1)a[sub]0[/sub]x[sup]r-2[/sup]+(r+1)ra[sub]1[/sub]x[sup]r-1[/sup]+(r+2)(r+1)a[sub]2[/sub]x[sup]r[/sup]+....)[br]+x(p0+p1x+p2x[sup]2[/sup]+....)(ra[sub]0[/sub]x[sup]r-1[/sup]+(r+1)a[sub]1[/sub]x[sup]r[/sup]+(r+2)a[sub]2[/sub]x[sup]r+1[/sup]+....)[br]+(q0+q1x+q2x[sup]2[/sup]+.....)(a[sub]0[/sub]x[sup]r[/sup]+a[sub]1[/sub]x[sup]r+1[/sup]+a[sub]2[/sub]x[sup]r+2[/sup]+.....)=0[br]x[sup]r[/sup]の係数の和は、r(r-1)a[sub]0[/sub]+p0ra[sub]0[/sub]+q0a[sub]0[br][/sub]=[r(r-1)+p0r+q0]a[sub]0[/sub]=0 a[sub]0[/sub]≠0だから、r(r-1)+p0r+q0=0[br]rについて整理する。[br][b]r2+(p[sub]0[/sub]-1)r+q[sub]0[/sub]=0[br][/b]このrについての方程式を[b]決定方程式[/b]という。[br]rの解が重複解か?重複解でないときは2解の差が整数かどうかで対処の仕方が変わる。
2.ガンマ関数
ベッセルの微分方程式は熱、光、惑星の運動などの宇宙工学など幅広く使われる大切なものだといわれる。その解でガンマ関数という表現が登場するので、そこから調べてみよう。[br][br][b][size=150]<ガンマ関数の定義と性質とは>[br][/size][/b]ガンマ関数は階乗関数の一般化だとよく言われる。どういうことだろうか。[br]ガンマ関数は正の実数xについて、Γ(x)=∫t[sup]x-1[/sup]e[sup]-t[/sup] dt[0,∞]と定義される。[br]・x=1のとき[b]Γ(1)[/b]=∫t[sup]1-1[/sup]e[sup]-t[/sup] dt=∫e[sup]-t[/sup] dt=[-e[sup]-t[/sup]][0,∞]=0-(-1)=[b]1[/b][br][br]・部分積分∫Fg=FG-∫fGで、F=t[sup]x[/sup],g=e[sup]-t [/sup] とするとき、gを積分するとG=-e[sup]-t[/sup]、Fを微分するf=xt[sup]x-1[/sup][br] x=x+1のときΓ(x+1)=∫t[sup]x[/sup]e[sup]-t[/sup] dt=[-t[sup]x[/sup]e[sup]-t[/sup] ][0,∞]-∫-xt[sup]x-1[/sup]e[sup]-t[/sup]dt = x∫t[sup]x-1[/sup]e[sup]-t[/sup]dt=xΓ(x)[br][b] xが正の実数のとき、Γ(x+1)=xΓ(x)言い換えると、[b][color=#0000ff]Γ(x)=(x-1)Γ(x-1)[/color][/b][br][/b][br]・とくに、xが整数のときも成り立つから、Γ(2)=1Γ(1), Γ(3)=2Γ(2),....。[br][b] つまり、nが正の整数のとき、Γ(n)=(n-1)!(階乗関数)[br][/b][br]・x=1/2のときt=y[sup]2[/sup]とおくと、dt/dy = 2yからdt=2y dyで、 y=t[sup]1/2[/sup][br]Γ(1/2)=∫t[sup]1/2-1[/sup]e[sup]-t[/sup] dt[0,∞]=∫t[sup]-1/2[/sup]e[sup]-t[/sup] dt[0,∞]=∫y[sup]-1[/sup]e[sup]-y^2[/sup][sup][/sup] (2y dy)[0,∞] =2∫e[sup]-y^2[/sup]dy[0,∞]=2Iとおく。[br]I=∫e[sup]-y^2[/sup]dy[0,∞]は、J=∫e[sup]-y^2[/sup]dy[0,a]=∫e[sup]-x^2[/sup]dx[0,a]とおくと、[br]J[sup]2[/sup]=(∫e[sup]-x^2[/sup]dx[0,a])(∫e[sup]-y^2[/sup]dy[0,a])=∫∫[sub]D(a)[/sub]e[sup]-(x^2+y^2)[/sup]dxdy、 D(a)={(x,y)|x,yが0以上a以下の正方形}とする。[br]原点中心の第一象限の半径pの領域をE(p)とすると、E(a)≦D(a)≦E(√2 a)。[br]正方形が大小の四分円の弧にはさまれる。それぞれの領域での2重積分 e[sup]-(x^2+y^2)[/sup]もこの順になる。[br]ここで、極座標変換x=rcosθ,y=rsinθをして、2重積分の積分変数を置き換えよう。[br][b]ヤコビアン[/b]|{x[sub]r[/sub] x[sub]θ[/sub]}{y[sub]r[/sub] y[sub]θ[/sub]}|=x[sub]r *[/sub] y[sub]θ [/sub]-x[sub]θ*[/sub] y[sub]r[/sub]=cosθ r cosθ - (-rsinθ sinθ) =r(cos[sup]2[/sup]θ+sin[sup]2[/sup]θ)=[b]r[/b]となるね。[br]だから、関数f(x,y)=e[sup]-(x^2+y^2)[/sup]のx,yに極座標を代入して、dxdyを [b]r[/b] dθdrにおきかえると[br]∫∫[sub]E(a)[/sub]e[sup]-(x^2+y^2)[/sup]dxdy=∫[b]dθ[/b][π/2, 0] ∫e[sup]-r^2[b] [/b][/sup][b]rdr[/b][a,0]=π/4(1-e[sup]-a^2 [/sup])はa→∞でπ/4に収束する。[br]同様に∫∫[sub]E(√2a)[/sub]e[sup]-(x^2+y^2)[/sup]dxdyもπ/4に収束する。[br]だから、挟み撃ちで、J[sup]2[/sup]もπ/4に収束するから、Iは√(π/4)=1/2√πとできるね。[br]結局、[b]Γ(1/2)=2・1/2√π=√π[/b]。[br][br][color=#0000ff](例)[br][/color]Γ(2.5)=1.5Γ(1.5)=1.5・0.5Γ(0.5)=3/4[b]√π。[br][/b]x=[1,2,3,4,5]のとき、Γ(x)=[1,1,2,3,4][br]x=[0.5 , 1.5, 2.5, 3.5, 4.5, 5.5 ] =√π [1, 1/2, 3/4,15/8, 105/16, 1155/32 ]
ガンマ関数 y=Γ(x)
3.ベッセルの微分方程式
[b][size=150]<第1種関数>[/size][/b][br]mを非負の定数とするとき、[br]p(x)=x, q(x)=x[sup]2[/sup]-m[sup]2[/sup]が解析的で、ベッセルの微分方程式x[sup]2[/sup]y"+xy'+(x[sup]2[/sup]-m[sup]2[/sup])y=0を解きたい。[br]微分方程式B=[math]y''+\frac{p(x)}{x}y'+\frac{q(x)}{x^2}y=0[/math]の係数は解析的ではない。[br]解の1つをy=x[sup]r[/sup]Σa_0x[sup]n[/sup]=x[sup]r[/sup](a[sub]0[/sub]+a[sub]1[/sub]x+a[sub]2[/sub]x[sup]2[/sup]+....)=a[sub]0[/sub]x[sup]r[/sup]+a[sub]1[/sub]x[sup]r+1[/sup]+a[sub]2[/sub]x[sup]r+2[/sup]+.....(a[sub]0[/sub]≠0) rは複素数としよう。[br][br]y'=ra[sub]0[/sub]x[sup]r-1[/sup]+(r+1)a[sub]1[/sub]x[sup]r[/sup]+(r+2)a[sub]2[/sub]x[sup]r+1[/sup]+....[br]y"=r(r-1)a[sub]0[/sub]x[sup]r-2[/sup]+(r+1)ra[sub]1[/sub]x[sup]r-1[/sup]+(r+2)(r+1)a[sub]2[/sub]x[sup]r[/sup]+....[br]p(x)=x=p0+p1x+p2x[sup]2[/sup]+.....だから、p1=1で、他は0。[br]q(x)=x[sup]2[/sup]-m[sup]2[/sup]=q0+q1x+q2x[sup]2[/sup]+.....だから、q0=-m[sup]2[/sup], q2=1で、他は0。[br][br]x[sup]2[/sup](r(r-1)a[sub]0[/sub]x[sup]r-2[/sup]+(r+1)ra[sub]1[/sub]x[sup]r-1[/sup]+(r+2)(r+1)a[sub]2[/sub]x[sup]r[/sup]+....)[br]+x(p0+p1x+p2x[sup]2[/sup]+....)(ra[sub]0[/sub]x[sup]r-1[/sup]+(r+1)a[sub]1[/sub]x[sup]r[/sup]+(r+2)a[sub]2[/sub]x[sup]r+1[/sup]+....)[br]+(q0+q1x+q2x[sup]2[/sup]+.....)(a[sub]0[/sub]x[sup]r[/sup]+a[sub]1[/sub]x[sup]r+1[/sup]+a[sub]2[/sub]x[sup]r+2[/sup]+.....)=0[br]この係数を具体化すると、[br]x[sup]2[/sup](r(r-1)a[sub]0[/sub]x[sup]r-2[/sup]+(r+1)ra[sub]1[/sub]x[sup]r-1[/sup]+(r+2)(r+1)a[sub]2[/sub]x[sup]r[/sup]+....)[br]+x(ra[sub]0[/sub]x[sup]r-1[/sup]+(r+1)a[sub]1[/sub]x[sup]r[/sup]+(r+2)a[sub]2[/sub]x[sup]r+1[/sup]+....)[br]+(x[sup]2[/sup]-m[sup]2[/sup])(a[sub]0[/sub]x[sup]r[/sup]+a[sub]1[/sub]x[sup]r+1[/sup]+a[sub]2[/sub]x[sup]r+2[/sup]+.....)=0[br]x[sup]r[/sup]の係数の和は、r(r-1)a[sub]0 [/sub]+ ra[sub]0[/sub]-m[sup]2[/sup]a[sub]0[/sub]=a[sub]0[/sub]([b]r[/b][sup]2[/sup]-m[sup]2[/sup][b])=0から、r=±mの2解をもつ。[/b][br]帰結C1: x[sup]r+1[/sup]の係数の和は、(r+1)r a[sub]1[/sub]+(r+1)a[sub]1[/sub]-m[sup]2[/sup]a[sub]1[/sub][sub][/sub]=[(r+1)[sup]2[/sup] -m[sup]2[/sup]]a[sub]1[/sub]=0 [br]帰結C2:x[sup]r+2[/sup]の係数の和は、(r+2)(r+1)a[sub]2[/sub]+(r+2)a[sub]2[/sub]-m[sup]2[/sup]a[sub]2[/sub]+a[sub]0[/sub]=0から、[(r+2)[sup]2[/sup] -m[sup]2[/sup]]a2+a0=0[br]帰結Ck:x[sup]r+k[/sup]の係数の和は、(r+k)(r+k-1)a[sub]k[/sub]+(r+k)a[sub]k[/sub]-m[sup]2[/sup]a[sub]k[/sub]+a[sub]k-2[/sub]=0から、[(r +k+m)(r+k-m)]a[sub]k[/sub]+a[sub]k-2[/sub]=0[br]・r=m(非整数)に対しては、 [br] 帰結C1から、mが非負ならa1=0。帰結C2から連鎖的に、奇数番目の係数a_odd=0[br] a0=Aとおくと、帰結Ckから、a[sub]k[/sub]=-a[sub]k-2[/sub]/[(r +k+m)(r+k-m)]=-a[sub]k-2[/sub]/[(k+2m)k][br] ここで、k=2sとおくと、a[sub]2s[/sub]=-a[sub]2s-2[/sub]/[(2s+2m)2s]=-a[sub]2s-2[/sub]/[4(m+s)s][br] Aに対して,sに1,2,3,4,5,....pを入れてこの漸化式を連続適用すると、[br] 基本解y=x[sup]r[/sup]Σa_nx[sup]n[/sup]の奇数番目の係数は0で、[br] 偶数番目の係数はa_even=a[sub]2p[/sub]=(-1)[sup]p[/sup]A/[2[sup]2p[/sup] p!(m+1)(m+2).....(m+p)][br] A=1/[2^mΓ(m+1)]とおくと、a_even=a[sub]2p[/sub]=(-1)[sup]p[/sup]A/[2[sup]2p+m[/sup] p!Γ(m+p+1)](mは非負の実数)[br] 解y=y1=x[sup]m[/sup]Σa_nx[sup]n[/sup] =[math]Σ\frac{(-1)^px^{2p+m}}{2^{2p+m}p!\Gamma(m+p+1)}=Σ\frac{(-1)^p}{p!\Gamma(p+m+1)}\left(\frac{x}{2}\right)^{2p+m}[/math] [p for 0 to ∞] を[br][b] m次の第1種ベッセル関数Jm(x)[/b]という。[br] mが整数でないなら、r=-mとおいて同様にして得られる基本解y2=J(-m)(x)はy1と一次独立になる。[br] y1とy2の1次結合が一般解となる。[br] [br]・r=m=n(整数)に対して[br] A=1/[2^n n!]とおくと、a_even=(-1)[sup]p[/sup]/[2[sup]2p+n[/sup] p!(n+p)!] (nは整数)[br] r=nとしたとき、x[sup]n[/sup]にp=0から∞の級数をかけて、[br] 解y=x[sup]r[/sup]Σa_nx[sup]n[/sup] =[math]x^nΣ\frac{(-1)^px^{2p}}{2^{2p+n}p!(n+p)!}[/math] [p for 0 to ∞ ] を[b]n次の第1種ベッセル関数Jn(x)[/b]という。[br] rが整数だとJ[sub]-n[/sub](x)は解J[sub]n[/sub](x)に従属します。そのために、ノイマン関数Nn(x)=[J[sub]n[/sub](x)cosπn-J[sub]-n[/sub](x)]/sinπnを[br] もう一つの基本解として、その1次結合を一般解とします。[br] このノイマン関数のことを第2種ベッセル関数ということもありますね。[br][color=#0000ff](例)[/color] [br] J0(x)=[math]x^0Σ\frac{(-1)^px^{2p}}{2^{2p}p!p!}=1-\frac{1}{2^2}x^2+\frac{1}{2^44^2}x^4-\frac{1}{2^66^2}x^6+-......\frac{(-1)^px^{2p}}{2^{2p}p!p!}+...[/math][br][br][color=#0000ff](例)[/color][br] J1(x)=[math]x^1Σ\frac{(-1)^px^{2p}}{2^{2p+1}p!\left(1+p\right)!}=x\left(\frac{1}{2}-\frac{1}{2^32}x^2+\frac{1}{2^54^23}x^4-\frac{1}{2^76^23}x^6+-......\right)=\frac{1}{2}x-\frac{1}{2^4}x^3+\frac{1}{2^8}x^5-\frac{1}{2^76^23}x^7+-......[/math][br][br][color=#0000ff](例)[/color][br] r=m=1/2を入れて、[br] J 1/2 (x) =[math]Σ\frac{(-1)^p}{p!\Gamma(p+\frac{3}{2})}\left(\frac{x}{2}\right)^{2p+\frac{1}{2}}[/math] [p for 0 to ∞ ][br]分母のp!は1からpまでのp個の積で、[br]分母のΓ(p+1+1/2)はΓ(1/2)に1/2,3/2,....(2p+1)のp+1個の積をかけたもの。[br](x/2)^(2p+1/2) はxの2p+1個の積/(2のp個の積と2のp+1個の積)×√2/xと等しい。[br]2のp個の積をp!のp個の要素に1対1につけると、2から2pまでのp個の偶数の積[br]2のp+1個の積を1/2,3/2,....(2p+1)のp+1個の要素に1対1につけると、[br]1から2p+1までのp+1個の奇数の積。[br]これらの積は、(-1)^p/[ Γ(1/2)×偶数の積×奇数の積] x^(2p+1)*×√2/x[br][math]=\frac{(-1)^p}{\sqrt{\pi}\left(2p+1\right)!}x^{2p+1}\sqrt{\frac{2}{x}}[/math] pがΣの変数だから、それ以外を定数扱いにしてΣの前にだそう。[br] J 1/2 (x) =[math]Σ\frac{(-1)^p}{p!\Gamma(p+\frac{3}{2})}\left(\frac{x}{2}\right)^{2p+\frac{1}{2}}=\sum\frac{(-1)^p}{\sqrt{\pi}\left(2p+1\right)!}x^{2p+1}\sqrt{\frac{2}{x}}\text{=\sqrt{\frac{2}{\pi x}}}\sum\frac{(-1)^p}{\left(2p+1\right)!}x^{2p+1}[/math] [p for 0 to ∞ ][br]Σの中はsinxのマクローリン展開と同じになったね。[br][color=#0000ff] [b] J 1/2 (x) =√(2/πx) sin x [/b][br][/color](例)[br]同様にして、...............................[br][color=#0000ff] [b] J -1/2 (x) =√(2/πx) cos x [/b][/color]
第1種1/2次、-1/2次のベッセル関数 J1/2(x),J-1/2(x)
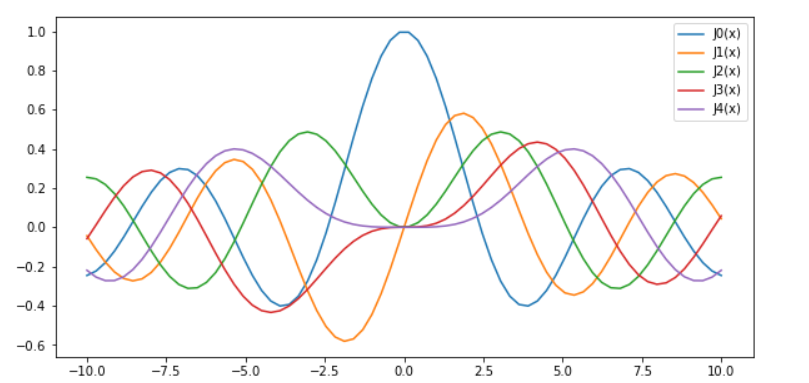
4.実装
[color=#9900ff][u][b][size=150]質問:第1種ベッセル関数をコードで実装するにはどうしたらよいですか。[br][/size][/b][/u][/color][br]やはり、科学計算のライブラリの多いpythonがおすすめです。[br]ベッセル関数は特殊関数という種類なのでscipy.specialを使います。[br]scipy.specialのjv(n,x)関数が、第n次の第1種ベッセル関数だね。[br][br]figで絵を枠を用意し、fig.add_subplot(111)が枠にプロットしょう。[br]xの値を[-10,10]区間を70等分くらいにすると線がなめらかになるでしょう。[br]yの値がjv(n,x)です。この(x,y)を使い、ax.plot(x, jv(v,x), label=...)でグラフをかきます。[br]#[IN]Python==============================[br][color=#0000ff]# 第1種ベッセル関数[br]import numpy as np[br]import matplotlib.pyplot as plt[br]from scipy.special import jv[br]fig = plt.figure(figsize=(10,5))[br]ax = fig.add_subplot(111)[br]x = np.linspace(-10, 10, 70)[br]for n in range(5):[br] ax.plot(x, jv(n, x), label=f"J{n}(x)")[br]ax.legend()[br][/color]#[OUT]=================================[br]
