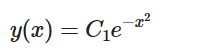
変数を分離しよう
★方向ベクトルたちをばらまく
0.微分方程式は関数さがし
[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/b][br][b][size=150]<微分方程式の解とは?>[/size][/b][br]普通、「[b]方程式[/b]」と言えば、等式を満たす数を求めるための情報のことだ。[br]平たく言えば「逆算」だね。[br](マスコミがよく使う「勝利の方程式」のような「法則、公式」という意味ではない。)[br][br]たとえば、「かけ算の方程式」を解く、つまり、かけ算の逆算をするには、かけ算の逆、割り算をする。[br]だから、[color=#0000ff]「微分の方程式」を解く、つまり、微分の逆算をするには、積分をすること[/color]になりそうだね。[br][br]代数方程式ならば、「[b][color=#0000ff]代数の等式[/color][/b]」という情報を満足させる「数」を求めることがゴールになる。[br]微分方程式ならば、「[b][size=150][color=#0000ff]微分の等式[/color][/size][/b]」という情報を満足させる「解」を求めることがゴールになるでしょう。「[b]微分方程式の解[/b]」は「数」ではなく、「[b]関数[/b]」です。[br][br]代数方程式を解くためには[b]解の公式、因数定理、因数分解、置換による次元下げ[/b]など、[br]数と数、数式と数式の「[b][color=#0000ff]関係性を利用した変形[/color][/b]」が重要だったね。[br][br]微分方程式を解くためには、関数と関数の「[b]関係性を利用した変形[/b]」が重要になるでしょう。[br]たとえば、[b][size=150][color=#0000ff]積分、[/color][/size][color=#0000ff][size=150]部分積分、置換積分、級数展開、フーリエ・ラプラスの変換(と逆変換)など[/size][/color][/b]が微分積分の関係性を利用した変形だね。[br][br]たとえば、f(x)=1という定数関数を[b]不定積分[/b]すると、F(x)=x+Cという関数になる。[br]だから、「[b]dy/dx=1」は微分方程式[/b]だ。[b]f(x)=x+C[/b]が解だというのは形式的にわかる。[br]ということで、積分の基礎知識が必要になりそうだから、確認しておこう。[br][br][b][size=150]<微積の基本公式の確認>[br][/size][/b](微分は->、不定積分は=>として定数Cは省略する)[br]べき関数 x[sup]n[/sup]=>1/(n+1) * x[sup]n+1[/sup][br]三角関数 sinx => -cos x , cos x =>sinx [br] sin(ax) => -1/a cos(ax) , cos(ax)=> 1/a sin (ax)[br]指数対数系 1/x => log[sub]e[/sub]|x| [br] e ^ax => 1/a * e ^ax[br]・合成の微分 f(g(x)) -> df/dg *dg/dx[br] からの[b]置換[/b]積分[br] g=g(x) とすると、f f(g(x)) dg/dx dx = ∫f(g) dg => F(g) [br] [color=#0000ff] (例)[/color]g=ax+b f(g)=e^gとみると、 ∫ae^(ax+b) dx = e^g + C[br]・積の微分 fg -> f'g + fg' から、 fg=∫(f' *g + fg') [br] からの積の積分([b]部分[/b]積分) ∫f' *g dx = - ∫f g' dx + f*gまたは、∫f *g' dx = f*g- ∫f' g dx[br] g',gを格上げしてg,Gとかくと、∫f *g dx =f*G - ∫f' G dx [br] 積f*gの片方だけ、積分形にして、もう片方は積分の中で微分する。[br]テーラー展開[br]e^x=Σ1/n! * x^n[br]sin x = Σ (-1)^n/ (2n+1)! *x ^(2n+1)[br]cos x = Σ (-1)^n/ (2n)! *x ^(2n)[br]オイラー等式[br]e^ix= sin x + i cos x[br][b][size=150][br]<微分方程式を解くことの意味は?>[br][/size][/b]では、これってどういう意味なのだろうか。[br]それが、上のアプレットからわかる。[br]図形的にみると、「dy/dx」は関数y=f(x)の曲線の点(x,y)における接線を表す関数y=f'(x)だった。[br]つまり、これって、[b]xy平面でのf(x)の変換の仕方についての一般的な情報[/b]ともいえるね。[br][br]この意味からすると、「dy/dx=1」は接線の傾きが一定の1になるのが関数y=f(x)ということになる。[br]つまり、f(x)はどこでも傾き1になる曲線、つまり、傾き1の直線ということだから、[br][b]一般的な解はf(x)=x+C[/b]になるね。この関数群が[color=#0000ff]一般解[/color]だ。[br]x=0のときのf(0)=0ならば、f(x)=xと限定できる。これが[color=#0000ff]特殊解[/color]になる。[br][br]出発点がx=0で、変化の仕方がdy/dx=1という特徴をもつ関数がf(x)=xだと限定できると、[br]x=0以外でのf(x)のふるまいが予測できるというのが微分方程式を解くことのよさになるでしょう。[br][br]代数方程式の場合は、1次、2次、3次と次数をメインに種類分けし、[br]種別に対する解の公式や解法を探るということをしてきた。[br][br]微分方程式はどうやってタイプ分けし、どう対処するのでしょうか。[br][br]それを探っていきましょう。
1.微分方程式のタイプ
[size=150][color=#0000ff]微分方程式についていろいろなネーミングやタイプ分けがあるので、[br]アレルギーが起きないように、さらっと外観しておこう。[br][/color][b]<種別>[br][/b][/size](階数)[br]代数方程式では、最高の次数がNならば、N次方程式と呼んだように、[br]微分方程式では、最高の[b]階数(微分の回数)[/b]がNならば、[b]N階[/b]方程式と呼ぶ。[br][br][b]・常微分[/b]方程式([b]ODE[/b])は、yをxで何回か微分したものを要素としている。[br]yが1変数xだけの関数のときだね。[br][b]・偏微分[/b]方程式は、それに対して多変数関数を微分した方程式。[br]yを3回微分したものをy(3)と書いたり、y'''と書いたりする。時間tの関数を微分3回微分したときは。[br]tの関数にドットを3つ乗せて表したりすることもあるね。[br][color=#0000ff](例)[br][/color]・yのn階微分をy[sup](n)[/sup]と書くことにすると、[b]y[sup](3)[/sup]+y[sup](2)[/sup]+y[sup](1)[/sup][/b]=f(x)+g(y)は3階[br]・[b]y[sup](2)[/sup][/b]=-ayは2階。yは単振動を表すことがある。[br]・上記の[b]y[sup](1)[/sup][/b]=-1は1階。[br][br][color=#0000ff](線形/非線形、同次/非同次、定数)[br][/color]・yのn階微分をy[sup](n)[/sup]と書き、[b]Akがxの関数[/b]、ΣAk*[b]y[sup](k)[/sup][/b]=0のとき、線形同次。[br] Akが定数なら、特に、定数線形同次というね。[br]・yのn階微分をy[sup](n)[/sup]と書き、Akがyの関数だったり、ΣAk*[b](y[sup](k)[/sup])[sup]j[/sup][/b]=0のように、[br] yの微分の項で1次(線形)でないものがあるとか、yの微分同士の積のが、[b]非線形[/b]同次。[br]・さらに、=0ではなく、=B(x)のとき、それぞれ非同次という。だから、[br] 線形非同次、非線形非同次などもあるね。[br][color=#0000ff](例)[/color][br](線形同次) [b]y[sup](2)[/sup][/b]+5[b]y[sup](1)[/sup][/b]=0, x[b]y[sup](2)[/sup][/b]+x[sup]2[/sup][b]y[sup](1)[/sup][/b]=y[br](線形[b][color=#ff0000]非同次[/color][/b])x[b]y[sup](2)[/sup][/b]+x[sup]2[/sup][b]y[sup](1)[/sup][/b]=[b][color=#ff0000]x[/color][/b][br]([b][color=#0000ff]非線形[/color][/b]同次) [b]y[sup](2)[/sup][/b]+[color=#0000ff]y[b]y[sup](1)[/sup][/b][/color]=0, [color=#0000ff]([b]y[sup](1)[/sup][/b])[sup]2[/sup][/color]+x[sup]2[/sup][b]y[/b]=0[br]([b][color=#0000ff]非線形[/color][/b][color=#ff0000]非同次[/color])[b][color=#0000ff]y[sup](1)[/sup]y[sup](3)[/sup][/color][/b]+x[b]y[sup](2)[/sup][/b]=[b][color=#ff0000]3x[sup]2[/sup][/color][/b][br][br][b][size=150]<基本型>[br][/size][/b]直接型、変数分離型、同次型、その他、などタイプ分けがある。[br][b]・直接型dy/dx=f(x)[/b][br]右辺の不定積分で、[b]y=F(x)+C[/b]と一般解を求めることができるね。[br][br][b][size=150][size=100]・変数分離型dy/dx=f(x)g(y)[br][/size][/size][/b]1/g(y) dy = f(x) dxのように、変数を等式の左右に分離できる型。[br]両辺に積分記号をつけた[size=150][b]∫[/b] 1/g(y)dy= [b]∫[/b]f(x)dxから、[b]G(y)=F(x)+C。[/b][/size][br][br][size=150]・[b]同次型dy/dx=f(y/x)[/b][/size][br]u=y/xを代入することで、変数分離形に還元できる。[br]
微分方程式。変数分離y'=-2xy
微分方程式。変数分離y'=x(2y-1)
微分方程式。変数分離y'=-4x/y
微分方程式。同次型y'=(x^2+y^2)/2xy
微分方程式。同次型y'=(2x-y)/(x-2y)
2.変数分離による解法
[b][size=150]<変数分離型dy/dx=f(x)/g(y)>[/size][/b][br][color=#0000ff]dy/dx=f(x)/g(y)を代数的に変数分離したf(x)dx=g(y)dyの両辺積分∫f(x)dx=∫g(y) dyから解が求められる。[br][/color]dy/dx=f(x)/g(y)でy=h(x)とすると、dy/dx=h'(x)=f(x)/g(h(x))だからf(x)=h'(x)g(h(x)) [br]したがって積分は∫f(x)dx=∫h'(x)g(h(x))dx。[br]置換積分dy= dy/dx dx= h'(x)dx より、右辺=∫ g(y)h'(x)dx= ∫g(y) dy。だから、∫f(x)dx=∫g(y) dy。[br][color=#0000ff](例)[/color][br]「[b]dy/dx=-2xy[/b]の一般解と(x,y)=(0,1)を通る特殊解」は?[br] 1/ydy=-2xdxの両辺積分∫1/ydy=∫-2xdxから、log|y|=-x[sup]2[/sup]+C |y|=e[sup](-x^2+C) [br][/sup]だから、y=±e[sup](-x^2+C) 。[/sup]一般解は[b]y=De[/b][sup][b](-x^2)[/b][/sup]、(x,y)=(0,1)からD=1で特殊解はy=e[sup](-x^2)[br][/sup][color=#0000ff](例)[/color][br]「[b]dy/dx=x(2y-1)[/b]の一般解と(x,y)=(0,1)を通る特殊解」は?[br] 1/(2y-1)dy=xdxの両辺積分1/2∫2/(2y-1)dy=∫xdxから、1/2log|2y-1|=1/2x[sup]2[/sup]+C |2y-1|=e[sup](x^2+2C)[/sup] [br]だから、y=±1/2e[sup](x^2+2C) [/sup]+1/2。一般解は[b]y=De[/b][b][sup](x^2)[/sup]+1/2[/b]、(x,y)=(0,1)からD=1/2で特殊解はy=(e[sup](x^2)[/sup]+1)/2[br][color=#0000ff](例)[/color][br]「[b]dy/dx=-4x/y[/b]の一般解と(x,y)=(0,2)を通る特殊解」は?[br] ydy=-4xdxの両辺積分∫ydy=∫-4xdxから、 1/2・y[sup]2[/sup]=-2x[sup]2[/sup]+C 一般解は(x/1)[sup]2[/sup]+(y/2)[sup]2[/sup]=C/2。[br](x,y)=(0,2)からC=2で、特殊解は(x/1)[sup]2[/sup]+(y/2)[sup]2[/sup]=1[sup]2[/sup]の[b]楕円[/b]。y=0除く[br][br][b][size=150]<同次型dy/dx=f(y/x)>[/size][/b][br][color=#0000ff]「dy/dx=f(y/x)ならu=y/xとして変数分離で両辺積分∫(1/x) dx =∫1/(f(u)-u) duで、u=y/xに戻せる。」[br][/color][size=100]u=y/xとおくとdy/dx=f(u)。y=xuの両辺微分[size=150]dy/dx=(xu)'[/size]=(x)'u+x(u)'=[size=150]u+x・du/dx[/size]。[br][/size]・2式からf(u)=u+du・x/dx 。 x/dx=(f(u)-u)/du。(1/x) dx =1/(f(u)-u) du [br] 両辺積分∫(1/x) dx =∫1/(f(u)-u) duして、uをy/xに戻せば一般解になるね。[br]・ y=mx型の解があるときはm=y/x=u(定数)。dy/dx=f(m)=mを満たすmをy=mxに代入すればよい。[br][color=#0000ff](例)[/color][br]「[b]dy/dx=[b](x[sup]2[/sup]+y[sup]2[/sup])/[/b]2xy[/b]の一般解」は?[br]u=y/xとおくとdy/dx=(1+(y/x)[sup]2[/sup])/(2y/x)=(1+u[sup]2[/sup])/2u。y=xuの両辺微分dy/dx=(xu)'=u+x・du/dx。[br]2式からu+x・du/dx=(1+u[sup]2[/sup])/2u。x/dx={(1-u[sup]2[/sup])/2u} /duこれから2u/(u[sup]2[/sup]-1) du=-1/x dxと変数分離。[br][math]\int\frac{2u}{u^2-1}du=-\int\frac{1}{x}dx[/math] から、 [math]log\left|u^2-1\right|=-log\left|x\right|+c[/math] となり、[math]x\left(u^2-1\right)=x\left(\left(\frac{y}{x}\right)^2-1\right)=\frac{y^2}{x}-x=C[/math] [br]だから、y[sup]2[/sup]-x[sup]2[/sup]=Cx。C=0の場合、y=±xも解([b]特異解[/b])となる。C=0も含めた一般解はy[sup]2[/sup]-x[sup]2[/sup]=Cx[br][color=#0000ff](例)[/color][br]「[b]dy/dx=(2x − y)/(x − 2y)[/b]の一般解」は?[br]u=y/xとおくとdy/dx=(2-y/x)/(1-2(y/x))=(2-u)/(1-2u)。y=xuの両辺微分dy/dx=(xu)'=u+x・du/dxから[br]u+x・du/dx=(2-u)/(1-2u)。x/dx={(2-u-u+2u[sup]2[/sup])/(1-2u} /duから(1-2u)/2(1-u+u[sup]2[/sup]) du=1/x dxと変数分離。 [math]\int\frac{1-2u}{1-u+u^2}du=2\int\frac{1}{x}dx[/math] から、 [math]-log\left|1-u+u^2\right|=2log\left|x\right|+c[/math] となり、[math]x^2\left(1-u+u^2\right)=x^2\left(1-\frac{y}{x}+\left(\frac{y}{x}\right)^2\right)=x^2-xy+y^2=C[/math] だから、x[sup]2[/sup]-xy+y2=C (C=0の場合も含む)
3.実装例と計算例
[color=#9900ff][u][b][size=150]質問:係数分離で解ける微分方程式をコードで解くにはどうしたらよいでしょうか。[br][/size][/b][/u][/color][br]科学技術の計算と視覚化の用途では、pythonかjuliaが適しています。[br]pythonユーザーが多いので、pythonを使います。[br]javascrptはrustやC++で作った部品をwebassenble化してweb表示するときには役立ちますが、高速計算や[br]大量データ処理が必要なければ、pythonにsympyをimportするのがよいでしょう。[br][br]sympyは微積分の機能があり、sympy.abcは変数を関数として設定する機能があります。[br][b]y = Function('y') [br]これで、yの文字や関数として読み取ります。[br][/b]しかし、dy/dxはこのままでは読み取れないのでDerivative(y(x), x)とかきましょう。[br]また、微分方程式がA=Bという等式だとしたら、[br]Eq(A,B)で渡します。それに名前をつけましょう。たとえば、deq。[br]微分方程式の解はdsolve(方程式、y(x))とかくと、「y=」の形式の解を返してくれます。[br]ただし、注意点があります。[br]A,Bによませる式では、yはy(x)とかいて、xの関数であることをいちいち明示することです。[br][br]やってみると、変数分離型でも同次型でも解けます。[br]y^2=Pとなる関数が解になるときは、y=の形の回答となり、わざわざ+sqrt(P),-sqrt(P)の2つを返してくるので見た目が期待とちがったりしますね。[br][br][IN]=======================================[br][b]from sympy.abc import *[br]from sympy import *[br]y = Function('y') # y=f(x)[br][/b][br][b]def dydxEq(fx):[br][/b]Eq(左辺,右辺)[br] deq = Eq(Derivative(y(x), x), fx)[br] return dsolve(deq, y(x))[br][IN]=======================================[br][color=#0000ff]dydxEq(-2*x*y(x)) #一般解はy=De(-x^2)[br][/color][OUT]=====================================[br]
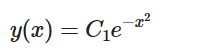
[IN]=======================================[br][color=#0000ff]dydxEq(x*(2*y(x)-1)) #一般解はy=De(x^2)+1/2[br][/color][OUT]=====================================
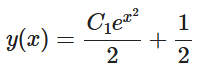
[IN]=======================================[br][color=#0000ff]dydxEq(-4*x/y(x)) #一般解は(x/1)^2+(y/2)^2=C/2[br][/color][OUT]=====================================[br][Eq(y(x), -sqrt(C1 - 4*x**2)), Eq(y(x), sqrt(C1 - 4*x**2))][br][IN]=======================================[br][color=#0000ff]dydxEq((x**2+(y(x))**2)/(2*x*y(x))) #一般解はy^2-x^2=Cx[br][/color][OUT]=====================================[br][Eq(y(x), -sqrt(x*(C1 + x))), Eq(y(x), sqrt(x*(C1 + x)))]
変数分離による解法とコードをみてきましたが、[br]現実問題としてどんな場面で[br]変数分離できる例が登場するかをみておきましょう。[br][br][b][size=150]<日本の人口>[/size][/b][br]時刻 t におけるある国の総人口を N(t) とする。[br]短い時間間隔 dt における出生数と死亡数は総人口と時間間隔に比例するから,[br]出生数=αNdt, 死亡数=βNdtとおける。[br]時間間隔 dt での人口の増加 dN=αNdt–βNdt=γNdtとかけるね。[br]これは微分方程式dN/dt=γN[br]∫1/N dN= ∫γ dt から、[b]logN=λt+C[/b][br][br]日本の令和5年(t=2023)出生率6.0/1000, 死亡率13.0/1000 ,人口N=121 193 394[br]γ=(6.0-13.0)/1000=-0.007。[br]log121193394=-0.007*2023+ C より、C=log121193394+0.007*2023=[br]import math[br]math.log(121193394)+0.007*2023[br]32.77389812516354[br][b]logN=λt+32.77とすると、N=e^(-0.007t) *e^32.77[br][/b][color=#0000ff]N(2050)=math.exp(-0.007* 2050)*math.exp(32.77)[br]=99931948.77012336[br][/color] ≒99931948[br]日本の人口は、2023年の1億2千万人から、2050年は9993万人になる?[br]そんなことはないかもしれません。[br]国土審議会によると9515万人と推定されています。[br]すでに高齢化社会なので、死亡率が高い人の割合が多く含まれるからでしょう。[br][br][b][size=150]<放射性物質の減少率>[br][/size][/b]放射性物質の量をN、時間ごとの減少率をγとすると、[br]人口モデルと同型の微分方程式dN/dt=-γN(γ>0)ができる。[br]∫1/N dN= -∫γ dt から、[b]logN=-λt+c、N=e^c*e^(-λt)=Ce^(-γt)[/b]となる。[br]半減期は、Ce^(-γx)=1/2Ce^(-γt) から、e^(-γx)=2^-1 *e^(-γt)。対数をとると、-yx=-log2- γt[br]log2=γ(x-t) から、[b]半減する年数x-t=log2/γ[/b][br][br]2011東日本大震災で福島第一原子力発電所から放出された主な放射性物質ヨウ素131、セシウム134、セシウム137、ストロンチウム90の4種類の半減期は順に約8日間、2年、30年、29年とします。[br]このうち、セシウム137の半減期が一番長いので、この物質が2011年に放出した量をN(2011)として、[br]2050にどれだけの量が残っているかを計算してみよう。[br]半減する年数x-t=log2/γ=30とする。γ=log2/30となる。N(2011)=Ce^(-log2/30 * 2011).[br]これから、C=N(2011)/e^(-log2/30 * 2011)[br]N(2050)=Ce^(-log2/30 * 2050)=N(2011)/e^(-log2/30 * 2011) * e^(-log2/30 * 2050)[br] =N(2011)*e^{(-log2/30 * 2050)-(-log2/30 * 2011)}[br] =N(2011)*e^{(-log2/30 * 39)}[br]import math[br][color=#0000ff]math.exp(-math.log(2)/30*39)[br]=0.4061261981781178[br][/color]まだ、約40%残るという計算です。[br]ただ、その場所にとどまっているわけではないので、拡散して濃度が薄まれば数字よりは付近にある量は[br]もっと減っているでしょう。
[b][size=150]<地球脱出速度>[br][/size][/b]地球の表面から発射された飛行体が地球の重力から逃れるための最小の初速vを求めたい。[br]地球、飛行体の質量をM,mとして、地球の中心からの飛行体への距離をrとしよう。[br]地球の半径をR,重力をg、万有引力定数をGとすると、[br]この飛行体が受ける力F=-ma=GMm/r[sup]2[/sup]から、加速度a=-GM/r[sup]2[/sup]となる。[br]発射時は、加速度はaを-gにおきかえ、rをRにおきかえて、g=GM/R[sup]2[/sup]から、GM=gR[sup]2[/sup]となる。[br]2式をまとめると、a=-(gR[sup]2[/sup])/r2=-g(R/r)[sup]2[/sup]となるね。[br]ここで、v=dr/dt, a=dv/dtだから、微分方程式はa=dv/dt=dv/dr*dr/dt=[br][b]v *dv/dr =-gR[sup]2[/sup]/r[sup]2[/sup][br][/b]変数分離して、v dv=-gR[sup]2[/sup]/r[sup]2[/sup] dr だから両辺積分∫v dv=-gR[sup]2[/sup]∫1/r[sup]2[/sup] dr[br]1/2v[sup]2[/sup]=gR[sup]2[/sup]/r+c これから、c=1/2v[sup]2[/sup]-gR[sup]2[/sup]/r[br]発射時点では、v=v0, r=Rだから、c=1/2 v0[sup]2[/sup]-gR[br]無限遠点r=∞で、v=0になるから、c=1/2v[sup]2[/sup]-gR[sup]2[/sup]/r→0-0=0。c=0[br]まとめると、c=1/2 v0[sup]2[/sup]-gR=0から、[b]v0=√(2gR)[/b][br]R:地球の平均半径 6372(km) [br]g:地球の重力 0.00980 (km/s[sup]2[/sup])[br]R=6372[br]g=0.00980[br][b]math.sqrt(2*g*R)[br][/b][color=#0000ff]11.175473144346059[br][/color]v0=11.2(km/s)の初速で、地球脱出ができるね。[br]
[color=#9900ff][b][u][size=150]質問:ここまでの現実的な問題の解に対して、具体的なイメージがわくような視覚化はどうやればよいでしょう。[br][/size][/u][/b][/color][br]微分方程式の解となる関数をgeogebraで表示しましょう。[br]独立変数となるtやrをxにした式にすることが必要だね。[br]独立変数をスライダーなどで変化させることで、求めた計算結果などの確認ができるでしょう。[br]