Funciones Exponenciales 1
Una vez dentro del terreno de las funciones exponenciales ya definidas en clase, estudiaremos algunas de ellas para extraer información acerca de su comportamiento.[br][br]Considera las funciones exponenciales [math]f:\mathbb{R}\longrightarrow\mathbb{R}^+\slash f\left(x\right)=2^x[/math] y [math]g:\mathbb{R}\longrightarrow\mathbb{R}^+\slash g\left(x\right)=\left(\frac{3}{2}\right)^x[/math][br][br]Represéntalas gráficamente en el siguiente applet y a continuación responde...[br]
Ten en consideración además la siguiente tabla de valores para estas funciones:
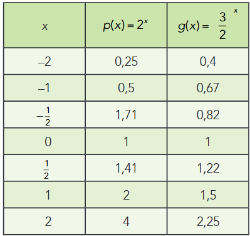
A partir de las gráficas obtenidas de la función f y la función g, podemos decir que las funciones:
En ambas, la imagen de 0 es:
Respecto a su signo podemos observar que sus imágenes son siempre:
Si observamos su crecimiento, decrecimiento, esto es, cómo se comportan sus imágenes cuando los valores de x aumentan, podemos concluir que ambas funciones son:
Una característica de estas funciones es la "rapidez" con la que crecen; a ese crecimiento vertiginoso se le llama crecimiento exponencial.
Observa que cuando x tiente a [math]-\infty[/math] las imágenes de estas funciones tienden a:
Lo que implica las funciones tienen una asíntota horizontal en la recta de ecuación:
A partir de tu trabajo, realiza un breve registro en tu cuaderno que contenga las funciones que has estudiado y una conclusión respecto a cada pregunta que has respondido.
Actividad modificada del libro: Matemática 4 Editorial Santillana. Cristina Ochoviet y Mónica Olave.[br]Imagen generada por IA generador de imágenes Copilot.