Solving Exponential Equations
WHAT YOU ALREADY KNOW
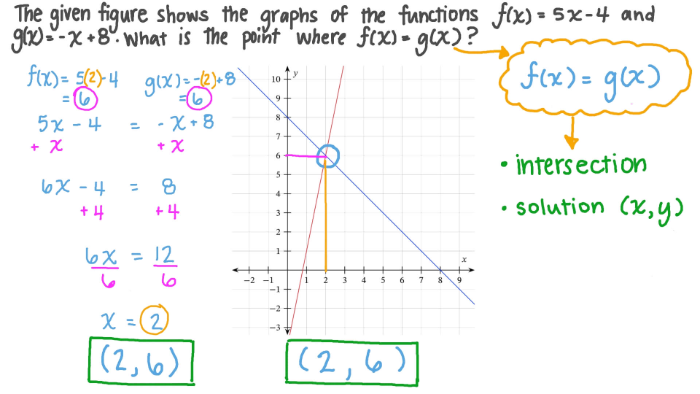
In Algebra 1 you have learned how to solve system of equations graphically.[br]In Algebra 2 you have learned that these equations can be of any form like quadratic functions. [br]In Pre Calculus the [b]ESSENTIAL QUESTION: How can you find the solution set of equations that involve exponential and logarithmic expressions?[/b][br]Below is an example to remind you what you used to do in Algebra 1 and 2.[br]

WHAT YOU WILL HAVE TO EXPLORE?
Given the two functions : [math]f\left(x\right)=2^{x-5}[/math]and [math]g\left(x\right)=2[/math]. [br]What is the solution set when f(x)= g(x) ?[br]Use the graph below to discover.[br]
Answer the following based on the graph above
The solution set of f(x) and g(x) is : [br]
Task 1: Exploring how to solve exponential equations with same base
Write down the steps for the solution below.
Are the steps above mathematically correct?
IDEA 2: Solving natural exponential equations with different base
[img]https://slideplayer.com/slide/8417517/26/images/3/Solving+exponential+equations+with+base+e.jpg[/img]
Try On your own:
Solve the following equation on your notebook [math]3e^{2x}-2=7[/math][br]Pick up the right answer from below
Choose the best answer