Verifiche formali di limiti e teoremi
Questo capitolo tratta il tema dei limiti da un punto di vista piuttosto avanzato. Fornisce infatti esempi svolti di verifiche formali di limiti, e mostra come attraverso questo procedimento sia possibile dimostrare proprietà generali dei limiti.[br][br][size=150][color=#ff0000][b]VERIFICA DI UN LIMITE IN CUI SI RICAVA UN'ESPRESSIONE PER [/b][/color][/size] [math]\Large{\textcolor{red}{\delta}}[/math] [br][br]Consideriamo il seguente limite[br][br][math]\Large{\lim_{x \to 8}\sqrt{x+1} = 3}[/math][br][br]Formuliamolo in termini logico algebrici: se vogliamo che il risultato [math]\large{\sqrt{x+1}}[/math] si avvicini abbastanza a 3, basta che la [math]\large{x}[/math] sia abbastanza vicina a 8[br][br][math]\Large{\textcolor{red}{\forall\ \varepsilon\gt 0\ } \textcolor{blue}{\exists \delta \gt 0\ } \mathbf{|}\ \textcolor{blue}{8-\delta \lt x \lt 8+\delta} \ \implies \ \textcolor{red}{3-\varepsilon \lt \sqrt{x+1} \lt 3+\varepsilon}}[/math][br][br]La parte in rosso riguarda l'avvicinamento lungo le [math]\large{y}[/math] (i risultati), mentre le parti in blu riguarda quelle lungo le [math]\large{x}[/math] (i valori di input).[br][br]Partiamo dalla condizione rossa, ovvero il risultato che vogliamo ottenere [br][br][math]\Large{\textcolor{red}{3-\varepsilon \lt \sqrt{x+1} \lt 3+\varepsilon}}[/math][br][br]Dobbiamo arrivare a dire che questa condizione è equivalente a quella blu, quindi dobbiamo isolare la [math]\large{x}[/math]. Eleviamo tutto alla seconda per sbarazzarci della radice, non prima di aver verificato che: [br][list][*][b]la radice esiste[/b]: OK! consideriamo [math]\large{x}[/math] vicine a 8, quindi [math]\large{x+1}[/math] è positivo[/*][*][b]i segni coerenti[/b]: OK! l'unica quantità che potrebbe essere negativa è [math]\large{3-\varepsilon}[/math], ma stiamo considerando [math]\large{\varepsilon}[/math] piccoli, quindi ragionevolmente minori di 3[/*][/list]Eleviamo quindi tutto al quadrato[br][br][math]\Large{\textcolor{red}{9+\varepsilon^2-6\varepsilon \lt x+1 \lt 9+\varepsilon^2+6\varepsilon} \quad \mathbf{\rightarrow} \quad \textcolor{red}{8+\varepsilon^2-6\varepsilon \lt x \lt 8+\varepsilon^2+6\varepsilon}}[/math][br][br]Nel secondo passaggio abbiamo tolto 1 a tutti i membri per isolare la x. Mettiamo in evidenza che stiamo affermando che [math]\large{x}[/math] si trova in un interno di 8: [br][br][math]\Large{8-\textcolor{blue}{(6\varepsilon-\varepsilon^2)} \lt x \lt 8+\textcolor{blue}{(\varepsilon^2+6\varepsilon)}}[/math][br][br]Che [math]\large{8+\textcolor{blue}{(\varepsilon^2+6\varepsilon)}}[/math] sia una quantità maggiore di 8 è abbastanza evidente.[br][br]Per [math]\large{8-\textcolor{blue}{(6\varepsilon-\varepsilon^2)}}[/math] bisogna prestare più attenzione. Intanto notiamo che abbiamo raccolto un segno meno per mettere in evidenza che stiamo [i]togliendo[/i] qualcosa ad 8. La quantità tra parentesi è ragionevolmente positiva: dato che consideriamo un [math]\large{\textcolor{red}{\varepsilon}}[/math] piccolo, moltiplicandolo per 6 otteniamo senz'altro una quantità maggiore di quella che otteniamo moltiplicandolo per se stesso.[br][br][b]Notiamo che le quantità tra parentesi non sono uguali, quindi abbiamo ottenuto un intorno non simmetrico.[/b]

L'intorno che abbiamo trovato si estende in modo differente prima di 8 rispetto a dopo 8. Se vogliamo prendere un raggio che ci garantisca di essere dentro in entrambe le direzioni, sarà sufficiente prendere il più piccolo dei due.
Se vogliamo trovare un raggio [math]\large{\delta}[/math] che garantisca di essere entro la zona blu in entrambe le direzioni, sarà sufficiente prendere il raggio minore dei due[br][br][math]\Large{\delta=min(6\varepsilon-\varepsilon^2, 6\varepsilon+\varepsilon^2)}[/math][br][br]In questo caso, per evidenti motivi, il raggio minore - e che quindi garantisce [i]sufficiente vicinanza ad 8[/i], è [math]\large{6\varepsilon-\varepsilon^2}[/math].[br][br][b]Abbiamo quindi verificato che se vogliamo che il risultato di [math]\large{\sqrt{x+1}}[/math] disti da 3 meno di [math]\large{\varepsilon}[/math], questo è equivalente a dire che basta considerare [math]\large{x}[/math] che distino da 8 meno di [math]\large{\delta = 6\varepsilon-\varepsilon^2}[/math].[/b][br][br][size=150][color=#ff0000][b]VERIFICA DI UN LIMITE IN CUI NON SI RIESCE A DARE UN'ESPRESSIONE A[/b][/color][/size] [math]\Large{\textcolor{red}{\delta}}[/math] [br][br]Consideriamo il seguente limite[br][br][math]\Large{\lim_{x \to 3}(x^2+3) = 12}[/math][br][br]Formuliamolo in termini logico algebrici: se vogliamo che il risultato [math]\large{x^2+3}[/math]si avvicini abbastanza a 12, basta che la [math]\large{x}[/math] sia abbastanza vicina a 3[br][br][math]\Large{\textcolor{red}{\forall\ \varepsilon\gt 0\ } \textcolor{blue}{\exists \delta \gt 0\ } \mathbf{|}\ \textcolor{blue}{3-\delta \lt x \lt 3+\delta} \ \implies \ \textcolor{red}{12-\varepsilon \lt x^2+3 \lt 12+\varepsilon}}[/math][br][br]La parte in rosso riguarda l'avvicinamento lungo le [math]\large{y}[/math] (i risultati), mentre le parti in blu riguarda quelle lungo le [math]\large{x}[/math] (i valori di input).[br][br]Partiamo dalla condizione rossa, ovvero il risultato che vogliamo ottenere [br][br][math]\Large{\textcolor{red}{12-\varepsilon \lt x^2+3 \lt 12+\varepsilon}}[/math][br][br]Si tratta di una catena di disequazioni di [b]secondo[/b] grado, che vanno risolte con il metodo della parabola; ci conviene quindi spezzarle nel sistema equivalente[br][br][math]\Large{\begin{cases}\textcolor{red}{x^2+3 \lt 12+\varepsilon}\\\textcolor{red}{ x^2+3 \gt 12-\varepsilon}\end{cases}\quad \rightarrow \quad \begin{cases}\textcolor{red}{x^2 \textcolor{blue}{-9-\varepsilon} \lt 0}\\\textcolor{red}{ x^2\textcolor{blue}{- (9-\varepsilon)} \gt 0}\end{cases}}[/math][br][br]Abbiamo usato il colore blu per mettere in evidenza che vi è un termine in [math]\large{x^2}[/math] e tutto il resto è un termine noto, anche se "un po' strano" perché vi compare la [math]\large{\varepsilon}[/math]; nella seconda disequazione abbiamo raccolto un [math]\large{-1}[/math] per mettere ancora più in evidenza questo termine.[br][br]Ognuna di queste disequazioni si risolve con il metodo della parabola. Partiamo della [b][color=#ff0000]prima[/color][/b]: si tratta di una parabola rivolta verso l'alto che tocca l'asse delle [math]\large{x}[/math] in [br][br][math]\large{x=\pm\textcolor{blue}{\sqrt{9+\varepsilon}}}[/math][br][br]Essendo interessati alla parte in cui la parabola è negativa dobbiamo prendere i valori [b][color=#ff0000]interni[/color][/b].[br]
Svolgendo calcoli analoghi con la [color=#0000ff][b]seconda[/b] disequazione[/color] troviamo una parabola ancora rivolta verso l'alto, che questa volta vale zero per [br][br][math]\large{x=\pm\textcolor{blue}{\sqrt{9-\varepsilon}}}[/math][br] [br]Questa volta però siamo interessati ai valori che rendono positiva la parabola, e quindi dobbiamo prendere quelli [b][color=#0000ff]esterni[/color][/b]. Mettendo a sistema i due risultati otteniamo[br]

Da notare che [math]\textcolor{blue}{\sqrt{9-\varepsilon}}[/math] viene PRIMA di [math]\textcolor{red}{\sqrt{9+\varepsilon}}[/math] perchè è un po' più piccolo. Per lo stesso motivo [math]\textcolor{blue}{-\sqrt{9-\varepsilon}}[/math] è meno negativo del corrispondente termine rosso e quindi è maggiore (ed è collocato alla sua destra).
Quindi affichè il risultato della funzione sia sufficientemente vicino a 12 la x deve essere in uno dei due intervalli verdi. Dato che ci interessa il caso in cui [math]\large{x \to +3}[/math], concentriamoci sull'intervallo che presenta estremi positivi (le radici senza il meno):[br][br][math]\Large{\textcolor{red}{\sqrt{9-\varepsilon} \lt x \lt\sqrt{ 9+\varepsilon}}}[/math][br][br]In questo caso non è semplice esprimere questo intervallo l'insieme di valori che vanno da "3 meno un certo raggio [math]\large{\delta}[/math]" e "3 più lo stesso raggio [math]\large{\delta}[/math] - ricorda che la radice di una somma [b][color=#ff0000]NON[/color][/b] è la somma delle due radici, e cioè ad esempio [math]\large{\sqrt{9+\varepsilon} \textcolor{red}{\mathbf{\neq}} \sqrt{9} + \sqrt{\varepsilon}}[/math] .[br][br]Ci conviene quindi semplicemente verificare che questa scrittura equivale a dire che [math]\large{x}[/math] si trova in un [i]certo[/i] intorno di [math]\large{3}[/math], senza cercare di capire [i]quale[/i] intorno. Questa operazione è più facile perché infatti [math]\large{\textcolor{red}{\sqrt{ 9+\varepsilon}}}[/math] è comunque appena più di [math]\large{3}[/math], mentre [math]\large{\textcolor{red}{\sqrt{ 9-\varepsilon}}}[/math] è appena di meno (anche se non sappiamo [i]quanto[/i]). [br][br]Un approccio alternativo è verificare che [math]\large{3}[/math] è sicuramente incluso tra questi due estremi, infatti se scriviamo [br][br][math]\Large{\textcolor{red}{\sqrt{9-\varepsilon} \lt 3 \lt\sqrt{ 9+\varepsilon}}}[/math][br][br]elevando al quadrato abbiamo [br][br][math]\Large{\textcolor{red}{9-\varepsilon \lt 9 \lt 9+\varepsilon} \rightarrow \textcolor{red}{-\varepsilon \lt 0 \lt \varepsilon}}[/math][br][br]che, essendo [math]\large{\varepsilon}[/math] positivo, è senz'altro vero. Quindi l'intervallo che contiene la [math]\large{x}[/math] contiene sicuramente anche il [math]\large{3}[/math], e quindi è un intorno di [math]\large{3}[/math].[br][br][b]Quindi abbiamo dimostrato che affermare che il risultato [math]\large{x}[/math] è in un intorno di 12 equivale a dire che [math]\large{x}[/math] è in un intorno di 3, e che quanto più vogliamo il risultato vicino a 12, quanto più vicino dovrà essere [math]\large{x}[/math] a 3. Il limite è quindi vero.[br][br][/b][b]ATTENZIONE: [/b]abbiamo visto che la verifica ci ha rivelato che il risultato della funzione si avvicina a [math]\large{12}[/math] anche quando la [math]\large{x}[/math] si trova nell'altro intervallo verde, cioè [br][br][math]\Large{\textcolor{red}{-\sqrt{9+\varepsilon} \lt x \lt-\sqrt{ 9-\varepsilon}}}[/math][br][br]Puoi verificare, in modo del tutto analogo a quanto fatto sopra, che questo intervallo è un intorno di [math]\large{-3}[/math]. Infatti la funzione tende a [math]\large{12}[/math] sia quando [math]\large{x}[/math] tende a [math]\large{3}[/math] che a [math]\large{-3}[/math].[color=#ff0000] La corretta applicazione del concetto di limite ci ha quindi rivelato delle proprietà aggiuntive della funzione, oltre a quella che stavamo verificando.[/color][br][br]
[size=150][b][color=#0000ff]TEOREMI SUI LIMITI[/color][/b][/size][br]Utilizziamo ora la verifica formale dei limiti per dimostrare proprietà generali dei limiti, cioè non riferite ad una funzione particolare.[br][br][size=150][color=#0000ff]LIMITE DI UNA FUNZIONE MOLTIPLICATA PER UNA COSTANTE.[br][/color][/size]Consideriamo una funzione [math]\large{g(x)}[/math] che si ottiene moltiplicando un'altra funzione [math]\large{f(x)}[/math] per una costante [math]\large{K}[/math], cioè [math]\large{g(x)=K\cdot f(x)}[/math]. Vogliamo dimostrare che [br][br][math]\Large{\ g(x)=K\cdot f(x) \land \lim_{x \to x_0} f(x) = L \implies \lim_{x \to x_0} g(x) = K \cdot L}[/math] [br][br]Detto in altri termini, per calcolare il limite di [math]\large{g(x)}[/math] basta moltiplicare per [math]\large{K}[/math] il limite di [math]\large{f(x)}[/math]. In termini ancora più diretti, se una funzione è moltiplicata per una costante, si può [i]portare fuori[/i] la costante fuori dal limite (sempre moltiplicandola).[br][br]Un esempio di applicazione di questo teorema ci permette di calcolare [br][br][math]\Large{\lim_{x \to 3} \textcolor{red}{5}\cdot 2^x =\textcolor{red}{5} \cdot \lim_{x \to 3} 2^x =\textcolor{red}{5} \cdot 8 = 40}[/math] [br][br][size=150][color=#0000ff]Dimostrazione[br][/color][/size]Le nostre [color=#0000ff]ipotesi[/color] sono che[br] [math]\Large{\textcolor{blue}{\begin{array}{l} 1)\ g(x)=K\cdot f(x)\\ 2) \lim_{x \to x_0} f(x) = L\end{array}}}[/math][br][br]riscriviamo esplicitamente la [color=#0000ff]ipotesi 2[/color] (usiamo i simboli [math]\large{\textcolor{blue}{\varepsilon_f}}[/math] e [math]\large{\textcolor{blue}{\delta_f}}[/math] per sottolineare che si tratta dei raggi definiti per il limite della funzione [math]\large{\textcolor{blue}{f(x)}}[/math]:[br][br][math]\Large{\textcolor{blue}{\forall\ \varepsilon_f\gt 0\ \exists \delta_f \gt 0\ } \mathbf{|} \ \textcolor{blue}{x_0-\delta_f \lt x \lt x_0+\delta_f \ \implies \ L-\varepsilon_f \lt f(x) \lt L + \varepsilon_f}}[/math][br][br]Vogliamo dimostrare che queste due condizioni sono sufficienti a dimostrare che allora vale la [color=#ff0000]tesi[/color], cioè che [math]\large{\textcolor{red}{\lim_{x \to x_0} g(x) = K \cdot L}}[/math]; utilizzando la ipotesi 1 possiamo riscriverla come [br][br][math]\large{\textcolor{red}{\lim_{x \to x_0} K\cdot f(x) = K \cdot L}}[/math][br][br]che scritta in forma esplicita (usiamo un'analoga notazione per indicare i raggi relativi ai limiti della funzione [math]\large{\textcolor{red}{g(x)}}[/math])diventa [br][br][math]\Large{\textcolor{red}{\forall\ \varepsilon_g\gt 0\ \exists \delta_g \gt 0\ } \mathbf{|} \ \textcolor{red}{x_0-\delta_g \lt x \lt x_0+\delta_g \ \implies \ K\cdot L-\varepsilon_g \lt K\cdot f(x) \lt K \cdot L + \varepsilon_g} \qquad (TH1)}[/math] [br][br]Abbiamo chiarito tutti gli elementi del teorema, siamo pronti a costruirne la dimostrazione.[br][br]Partiamo dall'ipotesi 2: essa afferma che [b][color=#0000ff]se prendiamo [math]\large{x}[/math] in un intorno di [math]\large{x_0}[/math] possiamo essere sicuri che[/color][/b] [br][br][math]\Large{\textcolor{blue}{\ L-\varepsilon_f \lt f(x) \lt L + \varepsilon_f}}[/math][br][br]Dato che da qui vogliamo dimostrare che (TH1) è vera, per avvicinarci ad essa moltiplichiamo tutto per [math]\large{K}[/math]. Per il momento supponiamo che sia [math]\large{K>0}[/math], così non dobbiamo invertire il verso delle disequazioni (puoi verificare che se prendiamo il caso in cui [math]\large{K<0}[/math] bisogna invertire il verso delle disequazioni, ma si giunge ad una conclusione identica). [br][br][math]\Large{\textcolor{blue}{\ K\cdot L-K\cdot \varepsilon_f \lt K\cdot f(x) \lt K\cdot L + K\cdot \varepsilon_f}}[/math][br][br]Vediamo che se definiamo [math]\large{\textcolor{red}{\varepsilon_g} = \textcolor{blue}{K\cdot \varepsilon_f}}[/math] otteniamo esattamente [br][br][math]\Large{\textcolor{blue}{\ K\cdot L-\textcolor{red}{\varepsilon_g} \lt K\cdot f(x) \lt K\cdot L + \textcolor{red}{\varepsilon_g}}}[/math][br][br]che è la tesi finale richiesta dalla (TH1). Quindi abbiamo visto che se consideriamo una [math]\large{x}[/math] appartenente ad un intorno di [math]\large{x_0}[/math], il risultato di [math]\large{K\cdot f(x)}[/math] rientra in un intorno di [math]\large{K \cdot L}[/math]. [br][br]In particolare per ottenere risultati che distino da [math]\large{K \cdot L}[/math] meno di [math]\large{\varepsilon_g}[/math] dobbiamo prendere lungo le [math]\large{x}[/math] un raggio pari a [math]\large{\delta_g = \delta_f\left (\varepsilon_f = \frac{\varepsilon_g}{K} \right)}[/math].[br][br][br]
[size=150][color=#0000ff]LIMITE DELLA SOMMA DI DUE FUNZIONI.[br][/color][/size]Consideriamo una funzione [math]\large{p(x)}[/math] il cui risultato si ottiene sommando quello di due funzioni; ad esempio sia [math]\large{p(x)=f(x)+g(x)}[/math]. Vogliamo dimostrare che il limite di [math]\large{p(x)}[/math] quando [math]\large{x \to x_0}[/math] coincide con la somma dei limiti di [math]\large{f(x)}[/math] e [math]\large{g(x)}[/math].[br][br]Formuliamo subito il teorema nelle sue ipotesi e tesi.[br][br]Le nostre [color=#0000ff]ipotesi[/color] sono che[br] [math]\Large{\textcolor{blue}{\begin{array}{l} 1)\ p(x)=f(x)+g(x)\\ 2) \lim_{x \to x_0} f(x) = L_f\\ 3) \lim_{x \to x_0} g(x) = L_g \end{array}}}[/math][br][br]mentre la [color=#ff0000]tesi[/color] è [br][br][math]\large{\textcolor{red}{\lim_{x \to x_0} p(x) = L_f + L_g}}[/math][br][br]cioè, utilizzando l'ipotesi 1), [br][br][math]\large{\textcolor{red}{\lim_{x \to x_0}[ f(x)+g(x) ] = L_f + L_g}}[/math][br][br]In termini espliciti, vogliamo quindi dimostrare che[br][br][math]\Large{\textcolor{red}{\forall\ \varepsilon_p \gt 0\ \exists \delta_p \gt 0\ } \mathbf{|} \ \textcolor{red}{x_0-\delta_p \lt x \lt x_0+\delta_p}}[/math][br][br][math]\Large{\textcolor{red}{ \implies \ L_f+L_g-\varepsilon_p \lt f(x) +g(x) \lt L_f+L_g + \varepsilon_p} \qquad (TH2)}[/math][br][br]Iniziamo la dimostrazione.[br][br]Riscriviamo le ipotesi 2 e 3 in modo esplicito, una sotto l'altra (usiamo due colori diversi per distinguerle meglio :[br][br][math]\Large{\begin{array}{lll} \textcolor{blue}{\forall\ \varepsilon\gt 0\ \exists \delta_f \gt 0\ } \mathbf{|}& \ \textcolor{blue}{x_0-\delta_f \lt x \lt x_0+\delta_f \ } \implies & \textcolor{blue}{\ L_f-\varepsilon \lt f(x) \lt L_f + \varepsilon} \\ \textcolor{#007700}{\forall\ \varepsilon\gt 0\ \exists \delta_g \gt 0\ } \mathbf{|}& \ \textcolor{#007700}{x_0-\delta_g \lt x \lt x_0+\delta_g \ } \implies & \textcolor{#007700}{\ L_g-\varepsilon \lt g(x) \lt L_g + \varepsilon} \end{array}}[/math][br][br]Da notare che partiamo dallo stesso [math]\large{\varepsilon}[/math] (lo scegliamo noi) ma ogni funzione ad esso associa un [math]\large{\delta}[/math] diverso, dato che ogni funzione è fatta in modo diverso - puoi vederlo meglio nell'immagine qui sotto. In ogni caso se consideriamo [math]\large{\delta = min(\delta_f, \delta_g)}[/math] entrambi i limiti saranno soddisfatti, quindi entrambe le catene di disequazioni finali saranno vere.
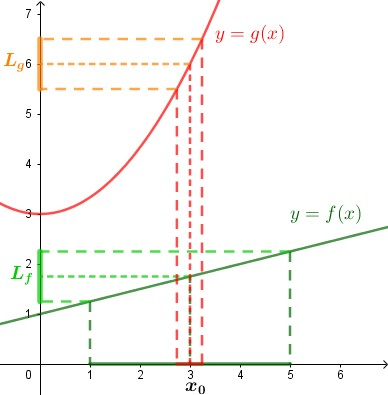
Quando x tende a [math]x_0[/math], [math]f(x)[/math] tende a [math]L_f[/math] e [math]g(x)[/math] tende a [math]L_g[/math].[color=#00ff00][br]Perché il risultato di [math]f[/math] cada nell'intervallo verde chiaro[/color], [color=#38761d][math]x[/math] deve essere nell'intervallo verde scuro di raggio [math]\delta_f[/math][/color].[br][br][color=#ff7700]Perchè il risultato di [math]g[/math] cada nell'intervallo arancio[/color], [color=#38761d][math]x[/math] [/color][color=#ff0000]deve essere nell'intervallo rosso di raggio [math]\delta_g[/math][/color].[br][br]Se prendiamo [math]x[/math] nell'intervallo più piccolo dei due (che in questo esempio è quello rosso), entrambe le condizioni sono garantite.
Sommandole membro a membro otteniamo[br][br][math]\Large{\textcolor{blue}{\ L_f} + \textcolor{#007700}{\ L_g} -\textcolor{blue}{\varepsilon} -\textcolor{#007700}{\varepsilon} \lt \textcolor{blue}{\ f(x)} + \textcolor{#007700}{\ g(x)} \lt \textcolor{blue}{\ L_f} + \textcolor{#007700}{\ L_g} +\textcolor{blue}{\varepsilon} +\textcolor{#007700}{\varepsilon} }[/math][br][br]Vediamo che definendo [math]\large{\textcolor{red}{\varepsilon_p} = 2\varepsilon }[/math] otteniamo[br][br][math]\Large{\textcolor{blue}{\ L_f} + \textcolor{#007700}{\ L_g} -\textcolor{red}{\varepsilon_p} \lt \textcolor{blue}{\ f(x)} + \textcolor{#007700}{\ g(x)} \lt \textcolor{blue}{\ L_f} + \textcolor{#007700}{\ L_g} +\textcolor{red}{\varepsilon_p} }[/math] [br][br]che non è altro che la tesi (TH2) che volevamo dimostrare. [br][br]Abbiamo quindi ottenuto che se vogliamo per la funzione somma un risultato vicino a meno di un certo [math]\large{\textcolor{red}{\varepsilon_p}}[/math] è sufficiente considerare una [math]\large{x}[/math] distante [math]\large{x_0}[/math] al più un raggio [math]\large{\delta_p = min \left (\delta_f \left(\frac{\textcolor{red}{\varepsilon_p}}{2}\right ), \delta_g\left (\frac{\textcolor{red}{\varepsilon_p}}{2}\right ) \right)}[/math] .




