Creating Painting Puzzles

Barbara Lichtenegger, Jun 25, 2018

[b]Workshop in Stockholm[/b] "Creating Painting Puzzles: Math, Art, Games and Technology" http://bridgesmathart.org/bridges-2018/ Bridges Conference, 25–29 July 2018

Table of Contents

  1. Introduction
    1. Abstract
    2. Painting Puzzle
    3. Panel "Los Mutilados"
  2. Artistic filters
    1. Creating a self-portrait and applying artistic filters
  3. Examples
    1. Painting Puzzle
    2. Bilderpuzzle
  4. Hints
    1. Coordinates
    2. Example of a coordinate system
    3. Coding

1.

Introduction

  • 1. Abstract
  • 2. Painting Puzzle
  • 3. Panel "Los Mutilados"

1.1.

Abstract

This workshop reproduces an activity developed with elementary students and aims to create a digital 8-piece sliding puzzle based on artistic self-portrait. The activity integrates mathematics, art, coding, and gaming by using Dynamic Geometry Software GeoGebra and other digital tools to edit artistic images. Workshop participants create their own digital 8-square puzzle, and have the opportunity to discuss implications for classroom practice, and how different steps can be adapted, implemented and extended to accommodate students of different abilities and interests. [br][br][br]
– Barbara Lichtenegger

1.2.

–

1.3.

–

2.

Artistic filters

  • 1. Creating a self-portrait and applying artistic filters

2.1.

Creating a self-portrait and applying artistic filters

Participants will take photos with their smartphone cameras. They will apply the Prisma app to edit their portrait using different artistic filters. These figures present examples how the appearance of a photograph can be completely changed to receive an artistic effect. The use of filters and the square-chop tools will add a personal and artistic touch to the final product integrating technologies into the project.[br]
Prisma. AI Powered Art Styles. For photo and video, 2018. [url=https://prisma-ai.com/]https://prisma-ai.com/[/url], retrieved on[br]2018-02-28.
Dividing the portrait into pieces
After creating artistic portraits, participants will digitally cut them into nine square pieces: [url=https://www.imgonline.com.ua/eng/cut-photo-into-pieces.php]https://www.imgonline.com.ua/eng/cut-photo-into-pieces.php[/url]
– Barbara Lichtenegger

3.

Examples

  • 1. Painting Puzzle
  • 2. Bilderpuzzle

3.1.

– Barbara Lichtenegger

3.2.

–

4.

Hints

  • 1. Coordinates
  • 2. Example of a coordinate system
  • 3. Coding

4.1.

Coordinates

In this step, participants will use the Cartesian Plane as reference to allocate the pieces and to translate them properly at GeoGebra interface. When playing the game it is necessary to click in a piece next to a blank square in order to make the piece move or slide to an empty space. To produce this effect, it is necessary to develop strategies on how to implement it. This offers an excellent opportunity to introduce mathematical concepts involving coordinates and translations.
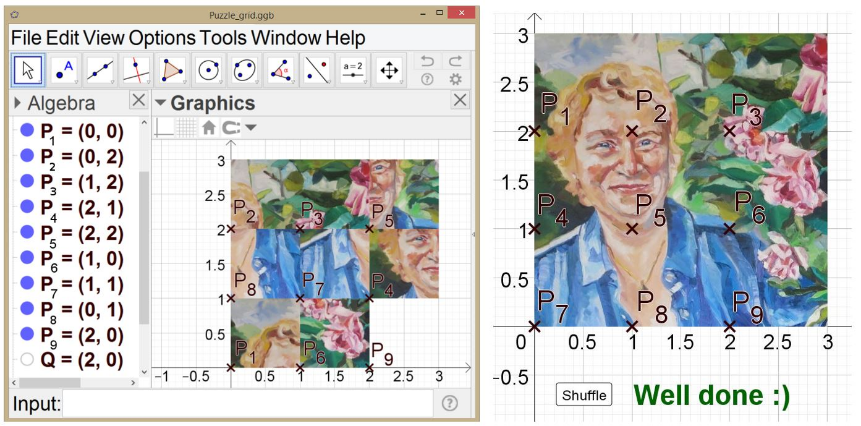
These figrues illustrate a possible solution of such a 3x3 sliding puzzle based on the previously discussed example.[br][br]
– Barbara Lichtenegger

4.2.

–

4.3.

–

Information