[size=150][b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br][/b]前回まで、微分方程式の解法をさまざま見てきた。[br]今回は、べき級数を利用して、微分方程式の解法につなげてみよう。[br][b][br][size=150][b]＜べき級数で微分方程式を解く＞[/b][/size][br][/b][/size][url=https://www.geogebra.org/m/a4dwkkhh#material/pesacxkb]べき級数[/url]と言えば、マクローリン級数（テーラー展開）が有名だ。[br][b]exp x= 1 + x + x^2/2! + x^3/3! + [br]cos x = 1 - x^2/2! + x^4/ 4! - + ....[br]sin x = x - x^3/3! + x^5/5! - + .... [br][/b]これらは、級数展開が無限に続く表現になっている。[br]f(x)のテーラー級数展開Σ(a_m (x-b)[sup]m[/sup])がx=bの半径Rの近傍で収束するとき、f(x)はx=bで解析的だという。上記のようにｂ＝０にした単純な形を[b]特にマクローリン展開[/b]と呼ぶ。マクローリン展開が収束する[br]ときは、x=0で解析的という。[br]ほかにも、べき級数展開の公式がある。[br]また、等比級数展開[br][b]1/(1-x)=1+x+x[sup]2[/sup]+x[sup]3[/sup]+....[/b]の両辺をxで０からｘまで積分すると[br][b]-lox(1-x)=x+1/2x[sup]2[/sup]+1/3x[sup]3[/sup]+..........[br][/b]xに-xを代入すると,[br][b]log(1+x)=x-1/2x[sup]2[/sup]+1/3x[sup]3[/sup]-+.......[br][/b]これから[b]1/2(ln(1+x)-ln(1-x))=x+1/3x[sup]3[/sup]+1/5x[sup]5[/sup]+.....[br][/b][br]微分方程式の解の関数もべき級数展開できたとすると[br]y=a_0+a_1x+a_2x^2+ a_3x^3+ ........... + a_kx^k+.....　 　 =[b]Σ(a_m x[sup]m[/sup]) [ m for 0 to ∞][/b][br]とおける。[br]y'= a_1 +2a_2x + 3a_3x^2 + .......... + ka_kx^(k-1) +......1 =[b]Σ(m a_m x[sup]m-1[/sup]) [ m for 1 to ∞][/b][br]y''= 2 a_2 + 3・2 a_3 x + ........ + k(k-1) a_k x^(k-2) + ...... [br] =[b]Σ(m(m-1) a_m x[sup]m-2[/sup]) [ m for 2 to ∞][/b][br]となる。[br]微分方程式y''+p(x)y'+q(x)y-r(x)=0の係数p(x),q(x),r(x)がx=aで解析的なら、解yもx=aで解析的だ。[br]定数や多項式はべき級数の形にかけて、その係数は０だから、収束するので解析的。[br]たとえば、微分方程式　[b]y' = 2xy[/b] [br]係数-2x=0+(-2)x+0x^2+0....でx=0において解析的。[br]関数を2x以外をすべてべき級数に置き換えてみよう。[br]left= a1 +2a2x + 3a3x^2 + .......... + kakx^(k-1) +......[br]right = 2x(a0+a1x+a2x^2+ a3x^3+ ........... + akx^k+.....)[br]左右の辺の同じ次数の項目の係数が等しいから、[br]a1=0 ,2a_2=2a_0 , 3a_3=2a_1, 4a_4=2a_2, 5a_5= 2a_3, 6a_6=2a_4[br]a_odd=0[br]a_even , a_0=Cとおくと、a_2k=C{1, 1,1/2, 1/3!, 1/4!,....} [br]これから、y=C(1+ 1x^2+1/2 x^4+ 1/3! x^6 + 1/4! x^8+....} =[b]C exp(x^2)[/b] が解となる。[color=#0000ff][br]（例）[/color][br]微分方程式[b]y''=-y[br][/b]係数-1=-1+0x + 0x^2+.......でx=0において解析的。[br]left= 2 a2+ 3*2 a3 x + 4*3 a4x^2 +5*4x^3........ + k(k-1) ak x^(k-2) + ......[br]right = -a0 -a1x - a2x^2 -a3x^3+ ........... + akx^k+.....　 係数比較[br]2*1a_2=-a_0, 3*2a_3=-a_1, 4*3a_4= -a_2, 5*4a_5=-a_3, 6*5a_6=-a_4 [br]a_0=A, a_1=Bとおくと[br]a_even=A{1,-1/2!, 1/4!, -1/6!, .....} , a_odd=B{1,-1/3!, 1/5!, -1/7!,......}[br]これから、[b]y=A cos x + B sin x[/b] [br]

[b][size=150]＜微分方程式＞[/size][/b][br][b]ｎが実数[/b]のときLの解ｙはｘの関数とする。[br]ルジャンドルの微分方程式L=[b][size=150](1-x[sup]2[/sup])y''-2xy' +n(n+1)y=0[/size][/b] の解を考える。[br][b][size=150]y''-2x/[b][size=150](1-x[sup]2[/sup])[/size][/b]y' +n(n+1)/[b][size=150](1-x[sup]2[/sup])[/size][/b]y=0[/size][/b][size=150]係数p(x)=[size=150]-2x/[size=150](1-x[sup]2[/sup])=-2x(1+x[sup]2[/sup]+x[sup]4[/sup]+.....),[/size][/size]q(x)=n(n+1)/(1-[size=150][size=150]x[sup]2[/sup][/size][/size])=n(n+1)(1+x[sup]2[/sup]+x[sup]4[/sup]+....)は解析的。[br][/size]だから、ｘ＝０は正則点だ。[br][b]正則点の付近ではL=0は、y=Σ(a_m xm) [ m for 0 to ∞]べき級数解をもつ[/b]。[size=150][/size][size=150][br][/size]式を簡単にみせるために n(n+1)＝kとおく。[br][b][size=150](1-x[sup]2[/sup])y''-2xy' +n(n+1)y[br]=y''- x[sup]2[/sup]y''-2xy' +ky=0[br][/size][/b]y=Σ(a_[sub]m[/sub] x[sup]m[/sup]) [ m for 0 to ∞]とするとき、y’’,y'もべき級数にして4項に代入して、x[sup]m[/sup]の係数を取り出そう。[br][br]+ky==>+k a[sub]m[/sub][br]-2xy'=-2xΣ(m a_m x[sup]m-1[/sup])から==> -2m a[sub]m[/sub][br][size=150][size=150][size=100]- x[sup]2[/sup]y''==> -m(m-1) a[sub]m[/sub][/size][br][size=150][size=100]y''=Σ(m(m-1) a[sub]m[/sub] x[sup]m-2[/sup])からmにm+2を代入して==>(m+2)(m+1) a[sub]m+2[/sub][br][/size][/size][/size][/size][b]x[sup]m[/sup]の係数は、(m+2)(m+1) a[sub]m+2[/sub] -m(m-1) a[sub]m[/sub]-2m a[sub]m[/sub]+k a[sub]m[/sub]=0[br][/b]まとめてみよう。[br](m+2)(m+1) a[sub]m+2[/sub]+ [-m(m-1) +(k-2m)]a[sub]m[/sub] [br]=(m+2)(m+1) a[sub]m+2[/sub]+ [n[sup]2[/sup]+n-m-m[sup]2[/sup]]a[sub]m[/sub][br]=(m+2)(m+1)a[sub]m+2[/sub] + (n-m)(n+m+1) a[sub]m[/sub]=0[br]だから、[br] [math]a_{m+2}＝-\frac{(n-m)(n+m+1)}{(m+2)(m+1)}a_m[/math] （いろんなnに対してｍを動かす漸化式）。[br]すると、[br] [math]a2=-\frac{n\left(n+1\right)}{2!}a0,a3=-\frac{\left(n-1\right)\left(n+2\right)}{3!}a1[/math], [br] [math]a4=-\frac{\left(n-2\right)\left(n+3\right)}{4\cdot3}a2=\frac{\left(n-2\right)n\left(n+1\right)\left(n+3\right)}{4!}a0[/math] [br] [math]a5=-\frac{\left(n-3\right)\left(n+4\right)}{5\cdot4}a3=\frac{\left(n-3\right)\left(n-1\right)\left(n+2\right)\left(n+4\right)}{5!}a1[/math] [br],,,,,,,,,,,,,,,,,,,,,[br] [math]a_{2s}=\left(-1\right)^s\frac{n-\left(2s-2\right)}{2s}\cdot\frac{n-\left(2s-4\right)}{2s-1}\cdot\frac{n-\left(2s-6\right)}{2s-2}.............\cdot\frac{n+\left(2s-5\right)}{3}\cdot\frac{n+\left(2s-3\right)}{2}\cdot\frac{n+\left(2s-1\right)}{1}a0[/math] [br] [math]a_{2s+1}=\left(-1\right)^s\frac{n-\left(2s-1\right)}{2s+1}\cdot\frac{n-\left(2s-3\right)}{2s}\cdot\frac{n-\left(2s-5\right)}{2s-1}\cdot.......\cdot\frac{n+\left(2s-2\right)}{3}\cdot\frac{n+2s}{2}a_1[/math]

[b][size=150]＜ルジャンドル関数＞[br][/size][/b]以上のようにして、[br][br]いろんな実数nに対して整数ｍを動かす漸化式[br] [math]a_{m+2}＝-\frac{(n-m)(n+m+1)}{(m+2)(m+1)}a_m[/math] [br]から、[br]mが偶数か奇数かで2系列の数列ができるので、[br][br]解はy=a_0 y0(x) + a_1 y1(x)とかける。[br][br]y(x)=a_0(1+a_2/a_0x^2+a_4/a_0x^4+........) + a_1(x+ a_3/a_1 x^3 + a_5/a_1 x^5 +........)[br]y0(x),y1(x)はそれぞれ、[b][color=#0000ff]ルジャンドル関数[/color][/b]という。[br][br]y0(x)=[math]1-\frac{n\left(n+1\right)}{2!}x^2+\frac{\left(n-2\right)n\left(n+1\right)\left(n+3\right)}{4!}x^4-......[/math] [s for 0 to ∞][br] [math]=\sum\left(-1\right)^s\frac{n-\left(2s-2\right)}{2s}\cdot\frac{n-\left(2s-4\right)}{2s-1}\cdot\frac{n-\left(2s-6\right)}{2s-2}.............\cdot\frac{n+\left(2s-5\right)}{3}\cdot\frac{n+\left(2s-3\right)}{2}\cdot\frac{n+\left(2s-1\right)}{1}x^{2s}[/math] [br][br]y1(x)=[math]x-\frac{\left(n-1\right)\left(n+2\right)}{3!}x^3+\frac{\left(n-3\right)\left(n-1\right)\left(n+2\right)\left(n+4\right)}{5!}x^5-.......[/math] [s for 0 to ∞][br] [math]=\sum\left(-1\right)^s\frac{n-\left(2s-1\right)}{2s+1}\cdot\frac{n-\left(2s-3\right)}{2s}\cdot\frac{n-\left(2s-5\right)}{2s-1}\cdot.......\cdot\frac{n+\left(2s-2\right)}{3}\cdot\frac{n+2s}{2}x^{2s+1}[/math] [br][br][color=#0000ff]（例）[/color][br]n=0のとき[br]y1(x)=[math]x-\frac{\left(-1\right)\left(+2\right)}{3!}x^3+\frac{\left(-3\right)\left(-1\right)\left(+2\right)\left(+4\right)}{5!}x^5+...[/math] [br]= [math]x+\frac{2}{3!}x^3+\frac{4!}{5!}x^5+...\sum\frac{\left(2s\right)!}{\left(2s+1\right)!}\cdot x^{2s+1}=x+\frac{1}{3}x^3+\frac{1}{5}x^5+.....=\frac{ln\left(1+x\right)-ln\left(1-x\right)}{2}=\frac{1}{2}ln\frac{1+x}{1-x}[/math] [br][br]n=1のとき[br]y0(x)=[math]1-\frac{1\left(1+1\right)}{2!}x^2+\frac{\left(1-2\right)1\left(1+1\right)\left(1+3\right)}{4!}x^4+\frac{\left(1-4\right)\left(1-2\right)1\left(1+1\right)\left(1+3\right)\left(1+5\right)}{6!}x^6+......[/math] [br]= [math]1-x^2-\frac{1}{3}x^4-\frac{1}{5}x^6-....=1-x\left(x+\frac{1}{3}x^3+\frac{1}{5}x^5+...\right)=1-x\left(\frac{1}{2}ln\frac{1+x}{1-x}\right)=1-\frac{x}{2}ln\frac{1+x}{1-x}[/math] [br][br]

[b][size=150]＜ルジャンドル多項式＞[br][/size][/b][b]解y=Σ(a_[sub]m[/sub] x[sup]m[/sup]) [ m for 0 to ∞]の[br][color=#0000ff]mは非負の整数を動く。[br]nも非負の整数を動くと限定してみよう。[br][br][/color][/b]漸化式に(n-m)の因数があるから、m番目が変数nになった時点でそのあとはゼロ倍になる。[br]つまり、添え字mを動かしても最高でもaの添え字はnで止まる。つまり解ｙはｎ次多項式になるね。[br][b]解ｙはｎ次多項式で、Pn(x)とかき、これをルジャンドル多項式[/b]という。[br]逆にa[sub]n[/sub]を仮定してa[sub]n-2[/sub], a[sub]n_4[/sub],.....とカウントダウンすることもできるはず。[br]最高次のa[sub]n[/sub]をたとえば、[br][math]a_n=\frac{(2n)!}{2^n\cdot(n!)^2}=\frac{2n\left(2n-1\right)\left(2n-2\right)\left(2n-3\right)......4\cdot3\cdot2\cdot1}{2n\left(2n-2\right)\left(2n-4\right)......4\cdot2\cdot n!}=\frac{\left(2n-1\right)\left(2n-3\right)....3\cdot1}{n!}=\frac{1}{1}\frac{3}{2}\frac{5}{3}\frac{7}{4}\cdot\cdot\cdot\cdot\cdot\frac{2n-1}{n}[/math][br]を仮定してみよう。つまり,自然数分の奇数をｎ個かけた値だ。[br][br]・次はカウントダウンの規則性を探ってみよう。[br]漸化式 [math]\frac{a_{m+2}}{a_m}＝-\frac{(n-m)(n+m+1)}{(m+2)(m+1)}[/math] の添え字mにnからのカウントダウンを入れよう。 [br] [math]if\left(m=n-2\right)\frac{a_n}{a_{n-2}}=-\frac{(n-\left(n-2\right))(n+\left(n-2\right)+1)}{(\left(n-2\right)+2)(\left(n-2\right)+1)}\Longrightarrow\frac{a_{n-2}}{a_n}=-\frac{n\left(n-1\right)}{2\left(2n-1\right)}[/math] だから、[br] 最高次の２つ下の係数は、[br] [math]a_{n-2}=-\frac{n\left(n-1\right)}{2\left(2n-1\right)}\frac{\left(2n\right)!}{2^n\left(n!\right)^2}=-\frac{n\left(n-1\right)2n\left(2n-1\right)\left(2n-2\right)!}{2^n\left(2n-1\right)2n\left(n-1\right)n\left(n-2\right)!\left(n-1\right)!}=-\frac{\left(2n-2\right)!}{2^n\left(n-2\right)!\left(n-1\right)!}[/math] [br] [math]if\left(m=n-4\right)\frac{a_{n-2}}{a_{n-4}}=-\frac{(n-\left(n-4\right))(n+\left(n-4\right)+1)}{(\left(n-4\right)+2)(\left(n-4\right)+1)}\Longrightarrow\frac{a_{n-4}}{a_{n-2}}=-\frac{\left(n-2\right)\left(n-3\right)}{4\left(2n-3\right)}[/math] だから、[br] 最高次の４つ下の係数は、[br][math]a_{n-4}=-\frac{\left(n-2\right)\left(n-3\right)}{4\left(2n-3\right)}\cdot-\frac{\left(n-2\right)!}{2^n\left(n-2\right)!\left(n-1\right)!}=.........=\frac{\left(2n-4\right)!}{2^n2\left(n-4\right)!\left(n-2\right)!}[/math] ............[br]これから推理して、 [math]a_{n-2m}=\left(-1\right)^m\frac{\left(2n-2m\right)!}{2^nm!\left(n-2m\right)!\left(n-m\right)!}[/math] [br]これをn-2m=1か0になるまで、mを動かして[br]ｘの（n-2m）次の係数としてたし上げた[b]ｎ次多項式がルジャンドルの多項式Pn(x)[/b]になるね。[br]nが偶数ならば最低次数は0まで、ｎが奇数なら最低次数は１までとなる。[br]mの最大値はn/２の商の切り捨てだから、ガウス記号[n/2]かシーリング関数を使う。[br][b]Pn(x)=Σ(a[sub]n-2m[/sub])[ m for 0 to [n/2]][/b] となる。[br][br]・では、P0(x)からP5(x)まで求めてみよう。[br]最高次の係数a_nの値は [math]a_n=\frac{1}{1}\frac{3}{2}\frac{5}{3}\frac{7}{4}\cdot\cdot\cdot\cdot\cdot\frac{2n-1}{n}[/math] だから、自然数分の奇数という分数の積だった。[br]n=0,1,2,3,4,5の順に[br] [math]a_1=\frac{1}{1},a_2=\frac{1}{1}\cdot\frac{3}{2}=\frac{3}{2},a_3=\frac{3}{2}\cdot\frac{5}{3}=\frac{5}{2},a_4=\frac{5}{2}\cdot\frac{7}{4}=\frac{35}{8},a_5=\frac{35}{8}\cdot\frac{9}{5}=\frac{63}{8}[/math] [br]漸化式からカウントダウンを入れよう。 [br] [math]\frac{a_{n-2}}{a_n}=-\frac{n\left(n-1\right)}{2\left(2n-1\right)}\frac{a_{n-4}}{a_{n-2}}=-\frac{\left(n-2\right)\left(n-3\right)}{4\left(2n-3\right)}[/math] だから、[br]n=0のとき、解は0次式でP0(x)=1[br]n=1のとき、解は1次式でP1(x)=1x[br]n=2のとき、解は2次式で、a_n=3/2, a_[sub]n-2[/sub]=3/2*[-2(2-1)/2(2*2-1)]=3/2*(-1/3)=-1/2から、P2(x)=3/2x[sup]2[/sup]-1/2[br]n=3のとき、解は3次式で、a_n=5/2, a_[sub]n-2[/sub]=5/2*[-3(3-1)/2(2*3-1)]=5/2*(-3/5)=-3/2から、P3(x)=5/2x[sup]3[/sup]-3/2x[br]n=4のとき、解は4次式で、a_n=35/8, a_[sub]n-2[/sub]=35/8*[-4(4-1)/2(2*4-1)]=35/8*(-6/7)=-15/4、[br] a_[sub]n-4[/sub]=-15/4*[-(4-2)(4-3)/4(2*4-3)]=-15/4*(-1/10)=3/8から、P4(x)=35/8x[sup]4[/sup]-15/4x[sup]2[/sup]-3/8[br]n=5のとき、解は5次式で、a_n=63/8, a_[sub]n-2[/sub]=63/8*[-5(5-1)/2(2*5-1)]=63/8*(-10/9)=-35/4、[br] a_[sub]n-4[/sub]=-35/4*[-(5-2)(5-3)/4(2*5-3)]=-35/4*(-3/14)=15/8から、P4(x)=63/8x[sup]5[/sup]-35/4x[sup]3[/sup]+15/8x

[u][b][size=150][color=#9900ff]質問：ルジャンドル多項式を求めるコードはどうやって作りますか。[br][/color][/size][/b][/u][br]scipyモジュールには[color=#0000ff]legendre多項式のｎ次式を求める関数legendre(n,x)[/color]があります。[br]sympyモジュールでは、latex形式で表示する[b]宣言init_printing()と関数display[/b]があります。[br]楽すぎてつまらないですね。[br][br]苦労したければ、ｎ次式として最高次の係数を自然数分の奇数の積を求め、[br]そこに次数を２ずつさげた係数の比をｎにあわせて次数が正である限り計算する。[br]それをｘにかけた式にして、latexにして表示する。[br]という３ステップを繰り返すことになるでしょう。[br][br]#[IN]Python===============[br][color=#0000ff]from scipy import *[br]from sympy import *[br]from sympy.abc import x[br][br]for i in range(10):[br] Legendre = legendre(i, x)[br] print(f"P{i}(x)=",end="")[br] init_printing()[br] display(Legendre)[br][/color]#[OUT]==================

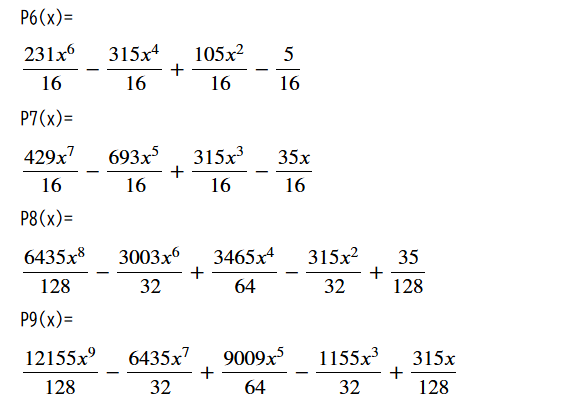
[b][size=150]＜ロドリグの公式＞[br][/size][/b][br]ルジャンドルの多項式Pn(x)を求めるには、(n+1)P[sub]n+1[/sub](x)=(2n+1)xP[sub]n[/sub](x)-nP[sub]n-1[/sub](x)[br]という漸化式を使う方法もありますが、[br][br]一気に求める公式、ロドリグの公式があります。[br]P[sub]n[/sub](x)=[math]\frac{1}{2^n\left(n!\right)}\frac{d^n}{dx^n}(x^2-1)^n[/math] [br][br][color=#9900ff][b][u][size=150]質問：ロドリグの公式をコードにするにはどうしたらよいですか。[br][/size][/u][/b][/color]lege=(x^2-1)^iのように多項式を定義して、[br]それを lege = [b]diff[/b](lege)をi回実行することで、i回微分すればよいね。[br]さらにそれを、2^i*factorial(i)で割りましょう。sympyには[b]factorial[/b]関数があるので[br]そのまま使います。[br]ただ、結果の式がとても複雑になるので、[br] Legend=Legend.[b]simplify[/b]()によって、式の単純化をしたものを表示します。[br][br]#[IN]Python=================================[br]from scipy import *[br]from sympy import *[br]from sympy.abc import x[br][br]print(f"P{0}(x)=",end="")[br]Lege=1[br]init_printing()[br]display(Lege)[br]for i in range(1,10):[br] lege=(x**2-1)**i[br] for j in range(1,i+1):[br] lege = diff(lege)[br] Legend= lege /( 2**i * factorial(i) )[br] Legend=Legend.simplify()[br] print(f"P{i}(x)=",end="")[br] init_printing()[br] display(Legend)[br][br]#[OUT]===============================[br]（省略）