
L’équation produit
[color=#ff0000][b][b][color=#ff0000]Dans cette activité, vous allez explorer la définition, Exemple et des propriétés pour résoudre une équation quotient [br][/color][/b][/b][/color]
Définition:
Toute équation de type [math]P\left(x\right)\times Q\left(x\right)=0[/math] où [math]P\left(x\right)[/math] et [math]Q\left(x\right)[/math] sont des expressions algébriques, est appelée équation-produit.

Remarque :
Nous rencontrerons plus particulièrement des équations-produits de la forme : [math]\left(ax+b\right)\left(cx+d\right)=0[/math]
Propriété n°1:
Si [b][color=#ff0000]a × b = 0[/color][/b] alors [color=#0000ff][b]a = 0[/b][/color] ou [b][color=#0000ff]b = 0[/color][/b].[br]Si un produit de facteurs est nul, alors l’un au moins des facteurs est nul.
Propriété n°2:
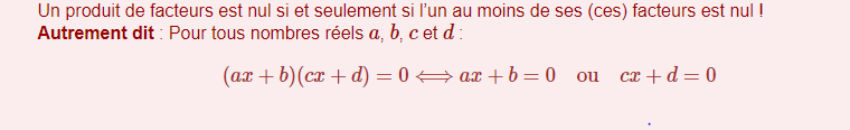
Exemple n°1:
Résoudre les équations suivantes dans [math]\mathbb{R}[/math][br]1°) [math]\left(E_1\right):\left(2x+3\right)\left(x-4\right)=0[/math][br]2°) [math]\left(E_2\right):\left(2x+3\right)\left(5x-4\right)=\left(2x+3\right)\left(4x-3\right)[/math]
Correction

