Exploring Hyperbolic Geometry
This GeoGebra book will go through a lesson on Hyperbolic geometry in comparison to Euclidean geometry. The lesson will discuss topics including: The Parallel Postulate, Curvature, Triangle Properties, and Triangle Construction.
Table of Contents
- 1. Introduction to Hyperbolic Geometry
- Purpose and Objectives
- Students START HERE
- History of Hyperbolic Geometry
- 2. Comparing Euclidean, Spherical, and Hyperbolic
- Euclidean vs. Spherical vs. Hyperbolic Geometry
- Origami Hyperbolic Paraboloid
- 3. Poincare Hyperbolic Disk
- What is The Poincare Disk
- Triangles Inside The Poincare Disk
- Equilateral Triangles in Poincare Disk
- Right Triangles in the Poincare Disk
- 4. Conclusion
- What Did We Learn & How is it Used?
Purpose and Objectives
Purpose of Learning About Hyperbolic Geometry
[center][color=#0000ff][b]The purpose of this GeoGebra book is to introduce students to Hyperbolic geometry through comparison to Euclidean geometry.[/b][/color][/center][center][color=#0000ff]The scope of this booklet does require some familiarity with hyperboloids.[br]All interactive constructions are done in The Poincare Model. A large focus of this book is triangles in Hyperbolic space.[br]The design of this booklet has questions that are intended for group discussion. [br]If this lesson is done asynchronously I would suggest making one of these questions a topic for a discussion post while also having them answer it in the GeoGebra activity.[/color][color=#3d85c6] [/color][/center]
Objectives for this Booklet
[list][*][color=#6aa84f]Apply previous knowledge about parallel lines in Euclidean geometry[br][/color][/*][*][color=#6aa84f]Apply previous knowledge about triangle properties in Euclidean geometry[br][/color][/*][*][color=#6aa84f]Identify key differences in the parallel postulate[br][/color][/*][*][color=#6aa84f]Explain the differences between zero, positive and negative curvature.[br][/color][/*][*][color=#6aa84f]Describe a line in hyperbolic geometry[br][/color][/*][*][color=#6aa84f]Describe properties of triangles in hyperbolic geometry[/color][br][/*][/list]
Euclidean vs. Spherical vs. Hyperbolic Geometry
Each of These Geometries Has a Different Type of Curvature
Here are the definitions for each type:[br][list][*][color=#0000ff]Positive Curvature:[/color][color=#38761d] A surface has positive curvature [/color][i][color=#93c47d]at a point[/color][/i][color=#38761d] if the surface curves away from that point in the same direction relative to the tangent to the surface, regardless of the cutting plane. Alternatively, the surface stays on one side of the tangent plane at that point. [/color](Thus the top of your head, the end of your finger, or the inside of your armpit are points of positive curvature.)[/*][/list][list][*][color=#0000ff]Negative Curvature: [/color][color=#38761d]A surface has negative curvature [/color][i][color=#93c47d]at a point[/color][/i][color=#38761d] if the surface curves away from the tangent plane in two different directions. [/color](The classic example is a saddle, which can be found on your body in the space between your thumb and forefinger, or along the inside of your neck.)[/*][/list][list][*][color=#0000ff]Zero Curvature:[/color][color=#38761d] A flat and infinite 2D plane[/color][/*][/list]
Below is a Representation of the Euclidean Surface
Based on the Definitions Above
What type of curvature does the [color=#ff7700]Euclidean surface[/color] have?
Explain your thinking. Discuss your thoughts with others if possible.
Below is a Representation of the Elliptical/Spherical Surface
Based on the Definitions Above
What type of curvature does the [color=#ff7700]Elliptical/Spherical surface[/color] have?
Explain your thinking. Discuss your thoughts with others if possible.
Below is a Representation of a Hyperbolic Saddle Surface
Based on the Definitions Above
What type of curvature does the [color=#ff7700]Hyperbolic surface[/color] have?
Explain your thinking. Discuss your thoughts with others if possible.
What is The Poincare Disk
The Poincare Disk: What is it?
[center][b]The Poincare Disk is one of many models of hyperbolic space. [/b][br]The four most common models of Hyperbolic space are: the Beltrami-Klein model, the Poincaré disk model, the Poincaré half-plane model, and the Lorentz or hyperboloid model[color=#0000ff][br][/color][color=#38761d]The Poincare Disk is a model of [br]2D hyperbolic geometry in which all points are inside the unit disk. Straight lines are represented either by circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.[/color][/center]
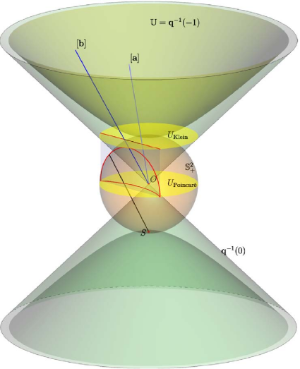
Below is a Display of Hyperbolic Space
[center][color=#6d9eeb]The large blue portion is a hyperboloid used to display hyperbolic space[/color][br][color=#ff7700]The orange ring is the Beltrami-Klein Disk [/color][br][color=#9900ff]The purple disk is our Poincare Disk[/color][/center][br]The parabolas created in the blue hyperbolic space are projected as straight lines on the orange Beltrami-Klein Disk, but they are projected as arcs of a circle on the purple Poincare Disk
Below is an Image Depicting the Models of Hyperbolic Space
Now Let's Look at What The Poincare Disk has:
[list=1][*][color=#38761d]A line is represented as an arc of a circle [/color][/*][*][color=#38761d]Diameters are also used inside the disk[/color][/*][/list]
Part 1
[color=#38761d]A line is represented as an arc of a circle[br][/color]
Part 2
[color=#38761d]Diameters are also used inside the disk[/color]
Construct a Diameter Using the Tool
This can be created from any point along the boundary of the disk
Use the Hyperbolic Line Tool
Considering what you have learned so far, what do you think is the purpose of using the Poincare Disk?
What questions do you still have about the Poincare Disk?
What Did We Learn & How is it Used?
Euclid's 5th Postulate
[left]Hyperbolic Geometry fails to meet the criteria for the 5th postulate, so the modified 5th postulate reads:[br][color=#38761d]"[i]For any infinite straight [url=https://mathworld.wolfram.com/Line.html]l[/url]ine L and any point P not on it, there are many other infinitely extending straight [url=https://mathworld.wolfram.com/Line.html]l[/url]ines that pass through P and which do not intersect L."[/i][/color][/left]
Curvatures of Various Geometries
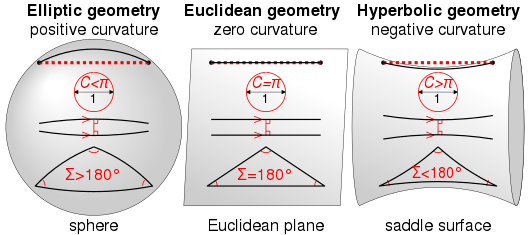
[center][/center]
[left]The photo above also depicts what we learned about the interior angles of a Hyperbolic triangle[br][color=#38761d]The sum of the interior angles is always less than 180 degrees[/color][br][/left]
[left]Another thing we learned about Hyperbolic triangles is that[br][math]a^2+b^2[/math]<[math]c^2[/math][/left]
How is Hyperbolic Geometry Used?
[left]There are some architectural structures designed using Hyperbolic Geometry[/left]
The Dulles Airport
[center][/center][left]https://www.flydulles.com/sites/flydulles.com/files/2021-08/inner_header_iad2.jpg [/left]
Designed by Eero Saarinen, the Dulles airport is the shape of a hyperbolic paraboloid.
Cooling Towers for Nuclear Reactors or Coal-Fired Power Plants
https://www.scienceabc.com/wp-content/uploads/2015/12/cooling-tower.jpg
[left]The hyperboloid is the design standard for all nuclear cooling towers and some coal-fired power plants. [br]They are built this way because the broad base allows for greater area to encourage evaporation, then narrows to increase air flow velocity. It then widens slightly to aid in mixing the moisture laden air into the atmosphere.[/left]
Some Other Hyperbolic Shapes You May Have Seen Before
Take a look at the pictures below. All are examples of objects with Hyperbolic shape
A Pringles Chip
https://twitter.com/ForecastyAI/status/1335912695405621249/photo/1
Lettuce Coral
https://comomath.wordpress.com/2012/06/17/ruffles-corals-and-the-hyperbolic-plane-3/
Lettuce Sea Slug (Elysia Crispata)
https://en.wikipedia.org/wiki/Elysia_crispata
Can you think of any objects with Hyperbolic Shape?
Feel free to use the internet to see what you can find, and share it below