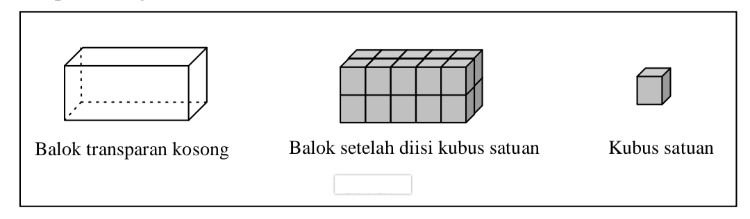
[justify][b]Balok[/b] merupakan suatu bangun tiga dimensi yang terbentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang diantaranya berukuran berbeda. Balok memiliki bentuk yang hampir sama dengan kubus, hanya saja memiliki ukuran panjang sisi yang berbeda-beda. Balok juga termasuk bagian dari prisma tegak segi empat dan bisa juga disebut "prisma siku-siku". [br][br][b]Volume Balok[br][/b]Volume bangun ruang yang diajarkan pertama kepada siswa adalah volume balok. Volume balok diajarkan pertama kali karena banyak benda-benda yang ditemui oleh siswa dalam kehidupan sehari-hari berbentuk balok. Misalnya ruang kelas, buku, kotak susu, kardus, lemari, dan lain sebagainya. Belajar mengenal volume balok bagi peserta didik dapat dilakukan secara induktif, yaitu dengan cara mengisi balok tanpa tutup dengan kubus satuan. Secara umum hal ini ditunjukkan dengan sebuah balok berongga tanpa tutup dan transparan serta kubus-kubus satuan seperti pada gambar dibawah ini. Kamudian kubus satuan diisikan ke dalam balok transparan sampai penuh yang membilang satu demi satu sampai hitungan terakhir. Pada gambar berikut, jumlah balok yang diisikan pada balok transparan hingga penuh sebanyak 20 kubus satuan. Hal ini dapat dinyatakan volume balok transparan dibawah ini adalah 20 kubus satuan.[/justify]

[justify]Setelah siswa mempunya pengalaman menghitung volume balok dengan cara membilang banyaknya kubus satuan yang dapat memenuhi balok berongga tersebut. Penurunan rumus balok sebaiknya dapat ditemukan sendiri oleh siswa dengan melihat volume beberapa balok seperti dalam gambar berikut.[/justify]

[justify][/justify][justify]Diharapkan setelah mengamati hasil yang telah diperoleh pada tabel diatas, siswa dapat menemukan hubungan antara kolom b dengan c, d, dan e, yaitu volume balok adalah panjang x lebar x tinggi. Jadi, Volume balok : [math]p\times l\times t[/math][br]Apabila [math]p\times l[/math] menyatakan luas alas balok, maka volume balok dapat juga dinyatakan sebagai berikut :[br][br][math]V=p\times l\times t[/math][br] [math]=\left(p\times l\right)\times t[/math][br] [math]=luasalas\times tinggi[/math][br][br]Untuk mengukur panjang suatu ruas garis diperlukan satuan panjang, satuan ukuran luas diperlukan untuk mengukur luas suatu daerah. Demikian juga untuk mengukur suatu bangun ruang diperlukan satuan volume yang biasanya berupa kubus satuan. Kubus satuan adalah kubus yang panjang rusuknya satu satuan panjang, misalnya 1 cm, 1 dm, atau 1 m. Satuan volume adalah "kubik" yang dituliskan dengan tanda pangkat tiga, misalnya sentimeter kubik (cm[sup]3[/sup]) atau meter kubik (m[sup]3[/sup]).[br][br]Untuk menentukan volume suatu cairan digunakan satuan khusus, seperti mililiter (ml), liter (l), dan kiloliter (kl). Biasanya apabila kita membeli susu atau bensin digunakan satuan liter, sedangkan jika membeli obat dengan satuan mililiter (ml) atau miligram (mg).[/justify]

[justify][b]Contoh :[br][/b]Jika suatu balok memiliki panjang 8,5 cm, lebar 9 cm, dan tinggi 5,5 kali lebarnya. Berapa volume balok tersebut?[/justify]

[i]Penyelesaian :[br][/i]Diketahui : panjang (p) = 8,5 cm[br]   lebar (l) = 9 cm[br]   tinggi (t) = 5,5 cm[br]Ditanya : berapa volume balok?[br]Jawab : [br] [math]V=p\times l\times t[/math][br]  = 8,5 x 9 x 5,5[br]  = 420,75[br]Jadi, volume balok adalah 420,75 cm[sup]3[br][br][br][/sup][b][justify]Setelah mempelajari materi bangun ruang balok dan contoh soal, sekarang saatnya Anda mengamati visualisasi balok dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk balok secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1 pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/justify][/b]

[justify]Animasi di atas merupakan tampilan dari bangun ruang balok yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan ukuran panjang, lebar, dan tinggi balok. Ketiga ukuran ini dilambangkan dengan [math]p[/math] (panjang), [math]l[/math] (lebar), dan [math]t[/math] (tinggi), yang dapat diubah-ubah untuk melihat bagaimana perubahan ukuran sisi memengaruhi volume balok.[br][br]Rumus volume balok dinyatakan dengan: [math]V=p\times l\times t[/math][br]Pada animasi ini, nilai panjang, lebar, dan tinggi dapat disesuaikan melalui penggeser. Misalnya, jika pada suatu kondisi: [math]p=5[/math] cm, [math]l=9,5[/math] cm, dan [math]t=7[/math] cm. Maka volume balok dihitung sebagai berikut: [math]V=5\times9,5\times7=332,5[/math] cm[sup]3[/sup].Volume yang ditampilkan pada animasi dihitung dengan mengalikan ketiga ukuran tersebut. Dari hasil ini, siswa dapat memahami bahwa volume suatu bangun ruang bergantung pada ukuran panjang, lebar, dan tinggi penyusunnya. Animasi ini memberi kesempatan kepada siswa untuk mengeksplorasi bagaimana volume berubah jika salah satu atau beberapa ukuran diperbesar atau diperkecil, sehingga memberi pemahaman yang lebih luas terhadap konsep volume balok secara umum.[br][br]Selain slider, animasi ini juga dilengkapi tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana ukuran sisi balok akan bertambah secara perlahan dan volume balok akan berubah secara otomatis sesuai nilai yang ditampilkan. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan melihat perubahan panjang, lebar, dan tinggi secara langsung serta pengaruhnya terhadap volume, siswa dapat memahami bahwa semakin besar ukuran balok, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa memahami konsep volume balok secara konkret dan visual.[/justify][br][b][br][br]Silakan lanjutkan dengan membaca materi tambahan yang tersedia melalui tautan website berikut. Materi tersebut disajikan secara interaktif dan mendalam untuk membantu Anda memahami topik dengan lebih baik. Bacalah dengan saksama dan coba kerjakan latihan soal yang tersedia di dalam website tersebut.[/b]

[b][justify]Setelah mempelajari materi dari website, pada bagian bawah halaman ini tersedia latihan soal tambahan. Kerjakan soal-soal tersebut dengan cermat dan teliti sebagai sarana untuk menguji dan memperkuat pemahaman Anda.[br][/justify][br][br]Latihan![/b]

[justify][b]Kubus[/b] adalah bangun ruang 3 dimensi yang memiliki 6 sisi berbentuk persegi yang kongruen. Dengan kata lain, setiap sisi kubus adalah persegi yang memiliki panjang sisi yang identik dan sudut antar sisi kubus adalah 90 derajat. Kubus juga termasuk dalam kategori prisma dengan alas berbentuk persegi atau bisa disebut juga "prisma siku-siku".[/justify]

[justify][b]Volume kubus[br][/b]Kita dapat menghitung volume kubus dengan menggunakan berbagai rumus berdasarkan parameter yang diberikan. volume kubus dapat dihitungn menggunakan panjang sisi dan ukuran diagonal kubus. Satuan yang digunakan untuk mengukur volume kubus dapat beragam, seperti milimeter kubik [math]\left(mm^3\right)[/math], sentimeter kubik [math]\left(cm^3\right)[/math], meter kubik [math]\left(m^3\right)[/math] dan lain sebagainya. Ini tergantung pada skala dan besarnya kubus yang sedang diukur.[br][br][/justify][b]a. Volume kubus menggunakan rumus panjang sisi[/b][br]Pada hakekatnya, sebuah kubus adalah sebuah balok yang semua rusuknya sama panjang (kongruen) atau [math]p=l=t[/math], sehingga rumus volume kubus dapat diturunkan dari rumus volume balok. Jika [math]s[/math] menyatakan panjang rusuk kubus, maka :[br][br]       [math]V_{_{kubus}}=s\times s\times s[/math] atau [math]V=s^3[/math]

Konsep untuk mendapatkan rumus volume kubus dapat dipahami dengan langkah-langkah berikut.[br][list][*]Coba bayangkan selembar kertas berbentuk persegi.[/*][*]Sekarang, luas yang ditutupi oleh lembaran persegi ini akan menjadi luas permukaannya, yaitu panjang dikalikan lebarnya. Sedangkan untuk persegi, karena panjang dan lebarnya sama, luas permukaannya akan menjadi "[math]s^2[/math]".[/*][*]Kubus dibuat dengan menumpuk beberapa lembar persegi diatas satu sama lain sehingga tingginya menjadi sama dengan panjang dan lebarnya, yaitu satuan "[math]s[/math]".[/*][*]Hal ini memberikan kita bahwa tinggi atau ketebalan kubus sebagai "[math]s[/math]".[/*][*]Maka dapat disimpulkan bahwa volume keseluruhan yang dicakup oleh kubus adalah [math]V=luasalas\times tinggi[/math] atau [math]V=s^2\times s[/math][/*][/list]

[justify][b]b. Volume kubus menggunakan rumus diagonal[br][/b]Volume kubus juga dapat diketahui secara langsung dengan rumus lain jika diagonal kubus diketahui.[/justify]

Langkah-langkah mencari volume kubus jika diketahui diagonal kubus sebagai berikut.[br][list][*]Diagonal kubus (d) adalah garis yang menghubungkan dua titik yang saling bersebrangan pada kubus. Jika sisi kubus kita sebut dengan [math]s[/math], maka panjang diagonal kubus [math]\left(d\right)[/math] dapat dihitung menggunakan rumus Phytagoras di ruang 3-dimensi, yaitu : [math]d=s\sqrt{3}[/math][br]Dimana : [math]d[/math] = panjang diagonal kubus, dan [math]s[/math] = panjang sisi kubus[/*][*]Untuk mencari volume kubus, kita perlu mengetahui panjang sisi kubus. Dari rumus diagonal diatas, kita dapat menyelesaikan untuk [math]s[/math] :  [math]s=\frac{d}{\sqrt{3}}[/math][br][/*][*]Volume kubus dihitung dengan rumus : [math]V=s^3[/math]. Jika kita subtitusikan nilai [math]s[/math] yang telah kita peroleh diatas ke dalam rumus volume, maka volume kubus dapat dihitung dengan rumus : [math]V=\left(\frac{d}{\sqrt{3}}\right)^3[/math] atau [math]V=\frac{d^3}{3\sqrt{3}}[/math][br][/*][/list]

[justify][b]Contoh :[br][/b]Hitunglah volume kubus jika panjang rusuknya 20 m![/justify]

[i]Penyelesaian : [br][/i][list][*]Diketahui : panjang rusuk (s) = 20 m[/*][*]Ditanya : berapa volume kubus?[/*][*]Jawab[i] : [/i][math]V=s^3=20^3=8000[/math][/*][/list]Jadi, volume kubus adalah 8000 [math]m^3[/math][br][br][br][justify][b]Setelah mempelajari materi bangun ruang kubus dan contoh soal, sekarang saatnya Anda mengamati visualisasi kubus dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk kubus secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1[/color] [color=#ff0000]pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/b][/justify]

[justify][/justify][justify]Animasi di atas merupakan tampilan dari bangun ruang kubus yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan panjang sisi kubus, yaitu sisi ke-1, sisi ke-2, dan sisi ke-3. Ketiga sisi ini dilambangkan dengan [math][/math]s, s[sub]2[/sub]​, dan s[sub]3[/sub]​, yang dapat diubah-ubah untuk melihat bagaimana panjang sisi memengaruhi volume kubus. Rumus volume kubus dinyatakan dengan: [math]V=s\times s\times s=s^3[/math]. Pada animasi ini, nilai sisi diambil dari tiga pengukuran, yaitu s=9. Semua kubus memiliki sisi yang sama, sehingga animasi ini dibuat dengan tujuan pembelajaran untuk memperlihatkan dampak perubahan ukuran sisi terhadap hasil volume yang dihitung.[br][br]Volume yang ditampilkan pada animasi dihitung dengan mengalikan ketiga sisi. Pada contoh animasi diatas volume kubus yaitu [math]V=9\times9\times9=729[/math] cm[sup]3 [/sup]. Dari hasil ini, siswa dapat memahami bahwa volume suatu bangun ruang bergantung pada panjang sisi-sisi penyusunnya. Animasi ini juga memberi kesempatan kepada siswa untuk mengeksplorasi bagaimana volume berubah bila sisi-sisi tersebut tidak sama, sehingga memberi pemahaman lanjutan terhadap konsep volume secara umum.[br][br]Selain slider, animasi ini juga dilengkapi tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana panjang sisi akan bertambah secara perlahan dan volume kubus akan berubah secara otomatis sesuai nilai sisi tersebut. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan melihat perubahan panjang sisi dan hasil volume secara langsung, siswa dapat memahami bahwa semakin besar ukuran sisi kubus, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa lebih mudah memahami konsep volume kubus secara konkret.[br][b][br][br][br]Silakan lanjutkan dengan membaca materi tambahan yang tersedia melalui tautan website berikut. Materi tersebut disajikan secara interaktif dan mendalam untuk membantu Anda memahami topik dengan lebih baik. Bacalah dengan saksama dan coba kerjakan latihan soal yang tersedia di dalam website tersebut.[/b][/justify]

[b]Setelah mempelajari materi dari website, pada bagian bawah halaman ini tersedia latihan soal tambahan. Kerjakan soal-soal tersebut dengan cermat dan teliti sebagai sarana untuk menguji dan memperkuat pemahaman Anda.[/b][b][br][br][br]Latihan![/b]

[justify][b]Prisma[/b] adalah sebuah bangun ruang 3-dimensi yang terdiri dari dua sisi yang kongruen berbentuk poligon yang terhubung dengan sisi tegak berupa segi empat. sisi-sisi poligon tersebut terletak di bagian atas dan bawah prisma, sedangkan sisi-sisi tegak menghubungkan sisi-sisi poligon tersebut. Dalam suatu prisma, sisi-sisi yang sejajar dan kongruen disebut sebagai "alas" dan "atap", sedangkan sisi-sisi yang lainnya disebut sebagai "sisi tegak". Prisma dikategorikan berdasarkan bentuk alasnya, seperti prisma segitiga, prisma segiempat, prisma segilima dan seterusnya.[br][br][/justify]

[b]Volume prisma[br][/b][justify]Untuk memperoleh rumus volume prisma, kita dapat memanfaatkan prinsip dasar tentang volume bangun ruang. Volume suatu benda dapat diperoleh dengan mengalikan luas alas dengan tinggi benda tersebut. Jika kita memandang prisma sebagai tumpukan salinan alas yang saling berdekatan, maka volume prisma dapat dianggap sebagai hasil perkalian luas alas dengan tinggi prisma. Tinggi prisma adalah jarak vertikal antara alas dan atap prisma (panjang sisi tegak yang menghubungkan alas adan atap). Secara umum, rumus volume prisma adalah :[/justify]       [math]V=L_{_{alas}}\times t[/math] [br]dimana, [list][*][math]V[/math] = volume prisma[/*][*][math]L_{_{alas}}[/math] = luas alas prisma[/*][*][math]t[/math] = tinggi prisma[/*][/list][br]Mari kita uraikan rumus volume prisma berdasarkan jenis alasnya.[br][br][b]a. Prisma Segitiga[br][/b]Prisma segitiga dalah prisma yang memiliki alas berbentuk segitiga. Misalkan alas prisma adalah segitiga dengan panjang alas [math]a[/math] dan tinggi alas segitiga [math]h_{_{alas}}[/math], serta tinggi prisma adalah [math]t[/math].[list][*]Luas alas segitiga dapat dihitung dengan rumus luas segitiga. [math]L_{_{alas}}=\frac{1}{2}\times a\times h_{_{alas}}[/math][/*][*]Jadi, volume prisma segitiga adalah [math]V=L_{_{alas}}\times t=\left(\frac{1}{2}\times a\times h_{_{alas}}\right)\times t[/math][/*][/list]

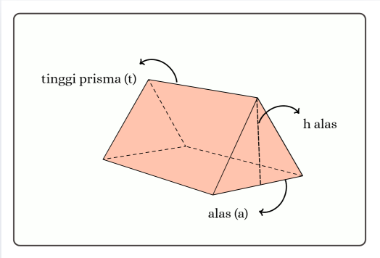
[justify][b]Contoh :[br][/b]Sebuah prisma dengan panjang alas segitiga adalah 6 cm, tinggi segitiga 4 cm, dan tinggi prisma adalah 10 cm. Hitunglah volume prisma tersebut![/justify]

[i]Penyelesaian :[br][/i]Diketahui : Panjang alas segitiga (a) = 6 cm[br]  Tinggi segitiga (h alas) = 4 cm[br]  Tinggi prisma (t) = 10 cm[br]Ditanya : berapa volume prisma tersebut?[br]Jawab : [math]V=\left(\frac{1}{2}\times a\times h_{_{alas}}\right)\times t[/math][br]   = (1/2 x 6 x 4) x 10[br]   = 12 x 10[br]   = 120[br]Jadi, Volume prisma tersebut adalah 120 [math]cm^3[/math][br][br][br][b][justify]Setelah mempelajari materi bangun ruang prisma segitiga dan contoh soal, sekarang saatnya Anda mengamati visualisasi prisma dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk prisma segitiga secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1 pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/justify][/b]

[justify]Animasi di atas merupakan tampilan dari bangun ruang prisma segitiga yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan ukuran bagian-bagian penting dari prisma segitiga, yaitu alas segitiga (a), tinggi segitiga (h[sub]a[/sub]), dan tinggi prisma (t). Ketiga ukuran ini dapat diubah-ubah untuk melihat bagaimana perubahan dimensi memengaruhi volume prisma segitiga.[br][br]Rumus volume prisma segitiga dinyatakan dengan: [math]V=\frac{1}{2}\times a\times h_a\times t[/math]. Pada animasi ini, nilai [math]a[/math], [math]h_a[/math], dan [math]t[/math] dapat diatur menggunakan penggeser. Misalnya, jika: [math]a=4[/math] cm, [math]h_a=6[/math] cm, dan [math]t=10[/math] cm. Maka volume prisma segitiga dihitung sebagai berikut: [math]V=\frac{1}{2}\times4\times6\times10=120[/math] cm[sup]3.[br][/sup][br]Volume yang ditampilkan pada animasi dihitung dengan menggunakan rumus di atas. Dari hasil ini, siswa dapat memahami bahwa volume suatu prisma segitiga bergantung pada ukuran alas segitiga, tinggi segitiga, dan tinggi prisma. Animasi ini memberi kesempatan kepada siswa untuk mengeksplorasi bagaimana volume berubah jika salah satu atau beberapa ukuran tersebut diubah, sehingga memberikan pemahaman yang lebih mendalam tentang konsep volume prisma segitiga.[br][br]Selain penggeser, animasi ini juga dilengkapi tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana ukuran akan bertambah secara perlahan dan volume prisma segitiga akan berubah secara otomatis sesuai nilai yang tampil. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan mengamati perubahan ukuran alas, tinggi segitiga, dan tinggi prisma secara langsung, siswa dapat menyimpulkan bahwa semakin besar ukuran bagian-bagian segitiga maupun tinggi prisma, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa memahami konsep volume prisma segitiga secara konkret dan visual.[/justify][br][b][br][br]b. Prisma Segiempat (persegi panjang atau persegi)[br][/b]Prisma segiempat memiliki alas berbentuk segiempat yang berupa persegi atau persegi panjang. Ini seperti kubus atau balok. Misalkan panjang alasnya adalah [math]p[/math] dan lebarnya adalah [math]l[/math], serta tinggi prisma adalah [math]t[/math].[list][*]Luas alas segiempat dihitung dengan rumus panjang kali lebar. [math]L_{_{alas}}=p\times l[/math][br][/*][*]Jadi, volume prisma segiempat adalah [math]V_{alas}=L_{alas}\times t=\left(p\times l\right)\times t[/math][/*][/list]

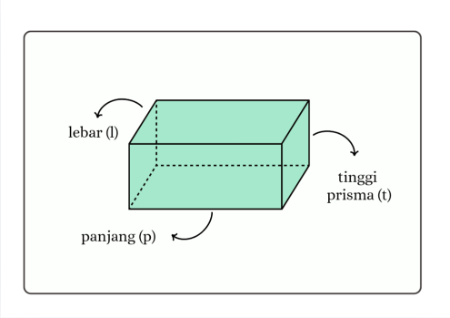
[justify][b]Contoh :[br][/b]Sebuah prisma segiempat memiliki panjang alas 8 cm, lebar alas 5 cm, dan tinggi prisma 12 cm. Hitunglah volume prisma tersebut![/justify]

[i]Penyelesaian :[br][/i]Diketahui : Panjang (p) = 8 cm[br]  Lebar (l) = 5 cm[br]  Tinggi prisma (t) = 12 cm[br]Ditanya : Berapa volume prisma tersebut?[br]Jawab : [math]V=\left(p\times l\right)\times t[/math][br]  = (8 x 5) x 12[br]   = 40 x 12[br]   = 480[br]Jadi, volume prisma segiempat tersebut adalah 480 [math]cm^3[/math][br][br][br][justify][b]Setelah mempelajari materi bangun ruang prisma segiempat dan contoh soal, sekarang saatnya Anda mengamati visualisasi kubus dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk prisma segiempat secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1 pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/b][/justify]

[justify]Animasi di atas merupakan tampilan dari bangun ruang prisma segiempat yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan ukuran panjang alas (p), lebar alas (l), dan tinggi prisma (t). Ketiga ukuran ini dapat diubah-ubah untuk melihat bagaimana perubahan ukuran memengaruhi volume prisma segiempat.[br][br]Rumus volume prisma segiempat dinyatakan dengan: [math]V=p\times l\times t[/math]. Pada animasi ini, nilai [math]p[/math], [math]l[/math], dan [math]t[/math] dapat diubah melalui penggeseran. Misalnya, jika: [math]p=8[/math] cm, [math]l=5[/math] cm, dan [math]t=12[/math] cm. Maka volume prisma segiempat dihitung sebagai berikut: [math]V=8\times5\times12=480[/math] cm[sup]3[/sup].[br][br]Volume yang ditampilkan pada animasi dihitung dengan mengalikan luas alas segiempat (p x l) dengan tinggi prisma. Dari hasil ini, siswa dapat memahami bahwa volume suatu prisma segiempat bergantung pada ukuran panjang dan lebar alas, serta tinggi prisma. Animasi ini memberi kesempatan kepada siswa untuk mengeksplorasi bagaimana volume berubah ketika salah satu ukuran diubah, sehingga memberikan pemahaman yang lebih luas mengenai konsep volume prisma.[br][br]Selain slider, animasi ini juga dilengkapi tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana ukuran akan bertambah secara perlahan dan volume prisma segiempat akan berubah secara otomatis mengikuti nilai yang tampil. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan melihat perubahan ukuran dan volume secara langsung, siswa dapat memahami bahwa semakin besar ukuran alas dan tinggi prisma, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa memahami konsep volume prisma segiempat secara konkret dan visual.[br][br][br][br][b]c. Prisma Segilima[br][/b][/justify][justify]Prisma segilima memiliki alas berbentuk segilima. Misalkan panjang sisi alas adalah [math]s[/math] dan tinggi prisma adalah [math]t[/math].[br][/justify][list][*]Luas alas segilima dapat dihitung dengan rumus luas segilima beraturan. Dimana sebuah segilima beraturan dapat dibagi menjadi 5 segitiga sama besar, yaitu dengan cara menarik garis dati titik pusat segilima ke setiap sudutnya. Jika luas 1 segitiga adalah [math]L_{alas}=\frac{1}{2}\times s\times a[/math] dimana : banyak segitiga = 5, setiap segitiga memiliki alas [math]s[/math], dan tinggi segitiga = apotema [math]a[/math].[/*][*]Jadi, luas seluruh segilima adalah [math]L_{alas}=5\times L_{segitiga}=5\times\left(\frac{1}{2}\times s\times a\right)[/math][/*][*]Jadi, volume prisma segilima luas alas segilima dikali tinggi prisma. [math]V=L_{alas}\times t=\frac{5}{2}\times s\times a\times t[/math][/*][/list]

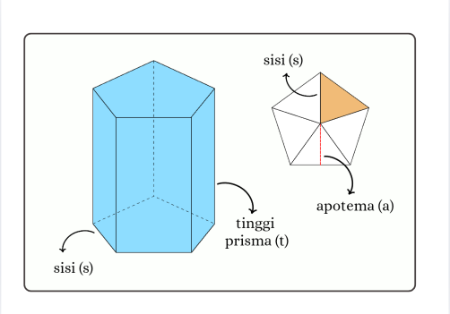
[justify][b]Contoh :[br][/b]Jika sebuah prisma berbentuk segilima beraturan dengan panjang sisi alasnya 6 cm, apotema alas 4 cm dan tinggi prisma 10 cm. Hitunglah volume prisma tersebut![/justify]

[i]Penyelesaian :[br][/i]Diketahui : Sisi segilima = 6 cm[br]  Apotema (a) = 4 cm[br]  Tinggi prisma (t) = 10 cm[br]Ditanya : berapa volume prisma tersebut?[br]Jawab : [math]V=\frac{5}{2}\times s\times a\times t[/math][br]   = 5/2 x 6 x 4 x 10[br]   = 5/2 x 240[br]   = 600[br]Jadi volume prisma tersebut adalah 600[math]cm^3[/math]

[justify][b][/b][/justify][justify][b]Silakan lanjutkan dengan membaca materi tambahan yang tersedia melalui tautan website berikut. Materi tersebut disajikan secara interaktif dan mendalam untuk membantu Anda memahami topik dengan lebih baik. Bacalah dengan saksama dan coba kerjakan latihan soal yang tersedia di dalam website tersebut.[/b][/justify]

[b][justify]Setelah mempelajari materi dari website, pada bagian bawah halaman ini tersedia latihan soal tambahan. Kerjakan soal-soal tersebut dengan cermat dan teliti sebagai sarana untuk menguji dan memperkuat pemahaman Anda.[/justify][br][br]Latihan![/b]

[justify][b]Limas[/b] adalah bangun ruang tiga dimensi yang memiliki alas berupa sebuah poligon dan sisi-sisi tegak yang berbentuk segitiga yang semuanya bertemu pada satu titik puncak. Puncak adalah titik di luar bidang alas yang menghubungkan semua sisi tegak. Ciri utama limas adalah adanya hubungan vertikal antara alas dan puncaknya, serta bentuk sisi tegaknya yang selalu berupa segitiga. Pada limas, alas bisa berupa poligon dengan berbagai jumlah sisi (segitiga, segiempat, segilima, dsb.), sementara sisi tegak berbentuk segitiga. Jumlah sisi tegaknya sama dengan jumlah sisi pada alas. Limas juga memiliki tinggi yang merupakan jarak vertikal antara puncak dan alas limas.[/justify][justify][b]Jenis-jenis Limas[br]a. Jenis limas berdasarkan bentuk alasnya[br][/b]Limas dapat dibedakan berdasarkan bentuk alasnya. Jenis limas yang paling umum adalah :[/justify][list=1][*]Limas segitiga yang memiliki alas berbentuk segitiga.[/*][*]Limas segiempat yang memiliki alas berbentuk persegi atau segiempat lainnya.[/*][*]Limas segilima yang memiliki alas berbentuk segilima.[/*][*]Limas segi-n yang memiliki alas berbentuk poligon, seperti segienam, segitujuh, segidelapan, dsb.[/*][/list][b]b. Jenis limas berdasarkan posisi puncak[br][/b]Selain berdasarkan bentuk lalas, limas juga dapat dibedakan berdasarkan posisi puncaknya, yaitu :[br][list=1][*]Limas Tegak. LImas tegak adalah limas yang puncaknya terletak tepat diatas titik pusat alas. Dalam limas tegak, garis tegak lurus dari puncak ke alas akan memotong alas pada titik pusatnya. Limas ini simetris, dengan sisi tegak yang berbentuk segitiga sama atau hampir sama. Contoh: Piramida dengan puncak berada tepat di atas pusat alas.[/*][*]Limas miring. Limas miring adalah limas yang puncaknya tidak terletak tepat di atas pusat alas. Dengan kata lain, tinggi limas pada limas miring tidak membentuk garis tegak lurus dari puncak ke pusat alas. Limas miring memiliki sisi tegak yang bentuk dan panjangnya bisa berbeda-beda.[/*][/list]

[b]Volume limas[br][/b][justify][b]Volume[/b] adalah ukuran yang menunjukkan berapa banyak ruang yang dapat diisi didalam suatu benda 3-dimensi. Misalkan bayangkan kamu memiliki sebuah kotak kosong. Jika kamu ingin mengisinya dengan air, pasir atau benda lainnya, volume-lah yang menentukan seberapa banyak isi yang dapat masuk kedalam kotak tersebut. Volume dihitung berdasarkan ruang yang ditempat oleh bangun tersebut, bukan hanya panjang dan lebar, tetapi juga tinggi. Sehingga [b]volume limas[/b] adalah besar ruang yang terletak di dalam limas. Volume limas tidak sebesar prisma, walaupun memiliki alas dan tinggi yang sama, karena bentuknya meruncing di pucuk. Volume luas lebih kecil dibandingkan dengan prisma, tepatnya sepertiga dari volume prisma dengan alas dan tinggi yang sama.[/justify][justify]Kenapa bisa begitu?[br]Untuk menjelaskan secara deskriptif, coba bayangkan sebuah prisma segiempat (seperti kotak besar atau balok). Lalu kamu membuat sebuah limas segi empat yang memiliki alas dan tinggi yang persis sama dengan prisma tersebut. Sekarang isilah limas dengan air atau pasir, lalu tuangkan isi limas tersebut kedalam prisma. Apa yang terjadi?[/justify][list][*]Kamu tuangkan sekali, prisma belum penuh[/*][*]Tuangkan kedua kali, prisma masih belum penuh[/*][*]Tuangkan ketiga kali, prisma baru penuh[/*][/list]Artinya, dibutuhkan tiga buah limas untuk mengisi volume satu prisma yang memiliki alas dan tinggi yang sama. Dari sini kita dapat menyimpulkan bahwa:[br]     [math]V_{Limas}=\frac{1}{3}\times V_{Prisma}[/math][br]     [math]V_{Limas}=\frac{1}{3}\times L.alas\times tinggi[/math]

[justify]Namun, untuk menghitung volume limas rumusnya berbeda-beda tergantung bentuk alasnya. Mari kita bahas setiap jenis limas secara mendetail dan bagimana cara memperoleh rumus volume limas.[br][br][b]1. Limas Segitiga[br][/b]Limas segitiga adalah limas yang memiliki alas berbentuk segitiga. Jadi, untuk memperoleh rumus volumenya kita perlu menghitung luas alas segitiga.[/justify][list][*]Luas alas. Untuk limas dengan luas alas segitiga, luas alasnya dihitung menggunakan luas segitiga : [math]L_{alas}=\frac{1}{2}\times a\times h_{alas}[/math] Dimana, [math]L_{alas}[/math] = luas alas yaitu segitiga [math]a[/math] =panjang alas [math]h_{alas}[/math] = tinggi alas[/*][*]Tinggi limas. Tinggi limas adalah jarak vertikal dari pucuk limas ke pusat alas segitiga. Misalnya jika tinggi limas adalah [math]t[/math], maka kita dapat langsung memasukkan tinggi limas tersebut kedalam rumus volumenya.[/*][*]Kemudian subtitusikan [math]L_{alas}[/math] dan tinggi limas [math]t[/math] : [math]V=\frac{1}{3}\times L_{alas}\times t[/math] [math]=\frac{1}{3}\times\frac{1}{2}\times a\times h_{alas}\times t[/math] [/*][*]Jadi, Rumus volume limas segitiga adalah : [math]V_{limas.segitiga}=\frac{1}{6}\times a\times h_{alas}\times t[/math] [/*][/list]

[b]Contoh :[/b][br]Sebuah limas memiliki alas berbentuk segitiga dengan panjang alas 6 cm dan tinggi segitiga 4 cm. tinggi limas adalah 9 cm. Berapakah volume limas?[br][br][i]Penyelesaian :[br][/i]Diketahu : panjang sisi alas (a) = 6 cm[br]   tinggi alas = 4 cm[br]   tinggi prisma = 9 cm[br]Ditanya : berapa volume limas?[br]Jawab : [math]V=\frac{1}{6}\times a\times h_{alas}\times t[/math] = 1/6 x 6 x 4 x 9 = 36[br]Jadi, volume limas tersebut adalah 36 [math]cm^{^3}[/math].[br][br][br][br][b][justify]Setelah mempelajari materi bangun ruang limas segitiga dan contoh soal, sekarang saatnya Anda mengamati visualisasi limas segitiga dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk limas segitiga secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1 pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/justify][/b]

[justify][/justify][justify]Animasi di atas merupakan tampilan dari bangun ruang limas segitiga yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan ukuran alas segitiga (a), tinggi segitiga alas (h[sub]a[/sub]), dan tinggi limas (t). Ketiga ukuran ini dapat diubah-ubah untuk melihat bagaimana perubahan ukuran memengaruhi volume limas segitiga.[br][br]Rumus volume limas segitiga dinyatakan dengan: [math]V=\frac{1}{3}\times\left(\frac{1}{2}\times a\times h_a\right)\times t[/math] atau lebih sederhananya [math]V=\frac{1}{6}\times a\times h_a\times t[/math]. Pada animasi ini, nilai [math]a[/math], [math]h_a[/math], dan [math]t[/math] dapat disesuaikan melalui penggeser. Misalnya, jika: [math]a=9[/math] cm, [math]h_a=6,4[/math] cm dan [math]t=8,9[/math] cm. Maka volume limas segitiga dihitung sebagai: [math]V=\frac{1}{3}\times\frac{1}{2}\times9\times6,4\times8,9=85,44[/math] cm[sup]3[/sup].Volume yang ditampilkan pada animasi dihitung berdasarkan perubahan ukuran sisi-sisi tersebut. Dari hasil ini, siswa dapat memahami bahwa volume suatu limas segitiga bergantung pada ukuran alas segitiga dan tinggi limas. Dengan mengubah-ubah penggeser, siswa dapat mengeksplorasi bagaimana perubahan satu atau lebih ukuran akan memengaruhi volume limas secara keseluruhan.[br][br]Selain slider, animasi ini juga dilengkapi dengan tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana ukuran akan bertambah secara perlahan dan volume limas segitiga akan berubah secara otomatis mengikuti nilai sisi yang tampil. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan melihat perubahan ukuran dan volume secara langsung, siswa dapat menyimpulkan bahwa semakin besar ukuran alas atau tinggi limas, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa memahami konsep volume limas segitiga secara konkret dan visual.[/justify][b][br][br]2. Limas Segiempat[br][/b]Limas segiempat memiliki alas berbentuk persegi atau persebi panjang. Misalkan kita ambil contoh limas segiempat dengan alas persegi lanjang.[list][*]Luas alas. Untuk limas segiempat dengan alas persegi panjang, luas alas akan dihitung menggunakan rumus : [math]L_{alas}=p\times l[/math] Dimana, panjang alas adalah [math]p[/math] dan lebar alas adalah [math]l[/math].[/*][*]Tinggi limas ([math]t[/math]) adalah jerak tegak lurus dari puncak limas ke pusat alas persegi panjang. Kita dapat langsung memasukkan tinggi limas tersebut kedalam rumus volumenya.[/*][*]Subtitusikan [math]L_{alas}[/math] dan tinggi limas [math]t[/math] : [math]V=\frac{1}{3}\times L_{alas}\times t[/math] [math]=\frac{1}{3}\times p\times l\times t[/math] [/*][*]jadi rumus volume limas segiempat adalah : [math]V_{limas.segiempat}=\frac{1}{3}\times p\times l\times t[/math][/*][/list]

[b]Contoh :[br][/b]Sebuah limas persegi panjang dengan panjang sisinya 10 cm dan lebarnya 7 cm. Jika volume limas adalah 140 cm[sup]3[/sup]. Hitunglah berapa tinggi limas tersebut?[br][br][i]Penyelesaian :[br][/i]Diketahui : panjang sisi (p) = 10 cm[br]   lebar (l) = 7 cm[br]   volume limas segiempat = 280 cm[sup]3[br][/sup]Ditanya : berapa tinggi limas?[br]Jawab : [math]V=\frac{1}{3}\times p\times l\times t[/math][br]  140 = 1/3 x 10 x 7 x t[br]  140 = 23,33 x t[br]   t = 140 / 23,33[br]   t = 6[br]Jadi, tinggi limas tersebut adalah 6 cm[br][br][br][b][justify]Setelah mempelajari materi bangun ruang limas segiempat dan contoh soal, sekarang saatnya Anda mengamati visualisasi limas segiempat dalam bentuk animasi interaktif menggunakan GeoGebra.[br][br]Animasi ini membantu Anda melihat bentuk limas segiempat secara nyata dan dari berbagai sudut pandang. [color=#ff0000]Lihat pada Bab 1 pada petunjuk animasi[/color] untuk memahami cara menjalankan dan mengubah tampilan objek. Gunakan kontrol yang tersedia untuk memutar, menggeser, atau mengubah sisi-sisinya sesuai petunjuk soal.[/justify][/b]

[justify]Animasi di atas merupakan tampilan dari bangun ruang limas segiempat yang interaktif. Pada animasi tersebut, terdapat tiga penggeser (slider) yang masing-masing menunjukkan ukuran panjang alas (p), lebar alas (l), dan tinggi limas (t). Ketiga ukuran ini dapat diubah-ubah untuk melihat bagaimana perubahan dimensi memengaruhi volume limas segiempat.[br][br]Rumus volume limas segiempat dinyatakan dengan: [math]V=\frac{1}{3}\times p\times l\times t[/math][br]Pada animasi ini, nilai [math]p[/math], [math]l[/math], dan [math]t[/math] dapat diatur menggunakan penggeser. Misalnya, jika: [math]p=7[/math] cm, [math]l=6[/math] cm, dan [math]t=9,1[/math] cm. Maka volume limas segiempat dihitung sebagai berikut: [math]V=\frac{1}{3}\times7\times6\times9,1=127,4[/math] cm[sup]3[/sup].[br][br]Volume yang ditampilkan pada animasi dihitung dengan mengalikan luas alas (p×lp \times lp×l) dengan tinggi limas, lalu dibagi tiga. Dari hasil ini, siswa dapat memahami bahwa volume limas segiempat sangat bergantung pada ukuran alas dan tinggi limas. Melalui animasi ini, siswa dapat mengeksplorasi bagaimana volume berubah ketika salah satu ukuran diubah, sehingga membantu memperkuat pemahaman mereka terhadap konsep volume limas.[br][br]Selain penggeser, animasi ini juga dilengkapi tombol [b]ON[/b] dan [b]OFF[/b]. Tombol [b]ON[/b] digunakan untuk mengaktifkan animasi otomatis, di mana ukuran akan bertambah secara perlahan dan volume limas segiempat akan berubah secara otomatis mengikuti nilai yang ditampilkan. Tombol [b]OFF[/b] digunakan untuk menghentikan pergerakan animasi kapan saja.[br][br]Dengan melihat perubahan ukuran panjang, lebar, dan tinggi limas secara langsung, siswa dapat menyimpulkan bahwa semakin besar ukuran alas atau semakin tinggi limas, maka semakin besar pula volume yang dihasilkan. Animasi ini memberikan pengalaman belajar yang interaktif dan menyenangkan, serta membantu siswa memahami konsep volume limas segiempat secara konkret dan visual.[br][b][br][br][br][br]3. Limas Segilima[br][/b]Limas segilima memiliki alas berbentuk segilima. Untuk menghitung volumenya, kita perlu menghitung luas alas segilima.[/justify][list][*]Luas alas. Untuk limas segilima menghitung luas alas menggunakan rumus luas segilima. Luas alas segilima dapat dihitung dengan rumus : [math]L_{alas}=\frac{1}{4}\times pangkat.sisi\times tinggi.apotema[/math]. Dimana pangkat sisi adalah panjang sisi alas segilima dikalikan 5 (karena segilima memiliki lima sisi) dan tinggi apotema [math][/math]adalah jarak dari pusat alas ke tengan setiap sisi. Misalkan pangkat sisi adalah [math]5s[/math] dan tinggi apotema adalah [math]t_a[/math], maka luas alas segilima adalah [math]L_{alas}=\frac{1}{4}\times5s\times t_a[/math][br][/*][*]Tinggi limas adalah jarak tegak lurus dari puncak limas ke pusat alas segilima. Tinggi ini biasanya disimbolkan dengan [math]t[/math][br][/*][*]Subtitusikan [math]L_{alas}[/math] dengan tinggi prisma [math]t[/math] : [math]V=\frac{1}{3}\times L_{alas}\times t[/math] [math]=\frac{1}{3}\times\frac{1}{4}\times5s\times t_a\times t[/math][br][/*][*]Jadi, volume limas segilima adalah : [math]V_{limas.segilima}=\frac{1}{12}\times5s\times t_a\times t[/math][/*][/list]

[b]Contoh :[br][/b]Tentukan volume limas segilima jika diketahui panjang alas 6 cm, tinggi apotema 4 cm serta tinggi prisma 10 cm![br][i]Penyelesaian :[br][/i]Diketahui : panjang alas (s) = 6 cm[br]   tinggi apotema (ta) = 4 cm[br]   tinggi prisma (t) = 10 cm[br]Ditanya : berapa volume limas?[br]Jawab : [math]V=\frac{1}{12}\times5s\times t_a\times t[/math][br]   = 1/12 x (5 x 6) x 4 x 10[br]   = 1/12 x 1200[br]  = 100[br]Jadi, volume limas tersebut adalah 100 cm[sup]3[/sup]

[b][justify]Silakan lanjutkan dengan membaca materi tambahan yang tersedia melalui tautan website berikut. Materi tersebut disajikan secara interaktif dan mendalam untuk membantu Anda memahami topik dengan lebih baik. Bacalah dengan saksama dan coba kerjakan latihan soal yang tersedia di dalam website tersebut.[/justify][/b]

[b][justify]Setelah mempelajari materi dari website, pada bagian bawah halaman ini tersedia latihan soal tambahan. Kerjakan soal-soal tersebut dengan cermat dan teliti sebagai sarana untuk menguji dan memperkuat pemahaman Anda.[br][/justify][br]Latihan![/b]